Обсуждение:Подсчет деревьев

Утверждение:

Число помеченных корневых деревьев с [math]k[/math] листьями и [math]m[/math] вершинами есть [math]P_{m,k} = k\cdot P_{m-1,k}+(m-k))\cdot P_{m-1,k-1}[/math]. Причем номер предка всегда меньше номера вершины. [math]P_{i,i} = 0, \forall i \in N[/math]; [math]P_{i,0} = 0, \forall i \in N, i \neq 1 [/math] не очень понятно. это ограничение или тебе так удобнее считать? базу утверждения лучше вынести в другое место

[math]\triangleright[/math]

Рассмотрим каждое слагаемое в данной формуле: 1) [math]k\cdot P_{m-1,k}[/math] обозначает, что мы можем подвесить ещё одну вершину к любому из [math]k[/math] листьев. Тогда количество листьев не изменится, а количество вершин увеличится на одну. 2) [math](m-k)\cdot P_{m-1,k-1}[/math] обозначает, что мы можем подвесить ещё одну вершину к любой вершине, не являющийся листом. Таких вершин [math](m-k)[/math]. Тогда количество листьев и количество вершин увеличится на один. Так как мы рассмотрели все возможные варианты присоединения новой вершины, то данная формула [math]P_{m,k} = k\cdot P_{m-1,k}+(m-k)\cdot P_{m-1,k-1}[/math] верна.

[math]\triangleleft[/math]

Пример
[math]m=1[/math] [math]m=2[/math] [math]m=3[/math] [math]m=4[/math]
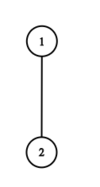
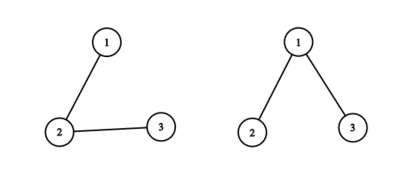
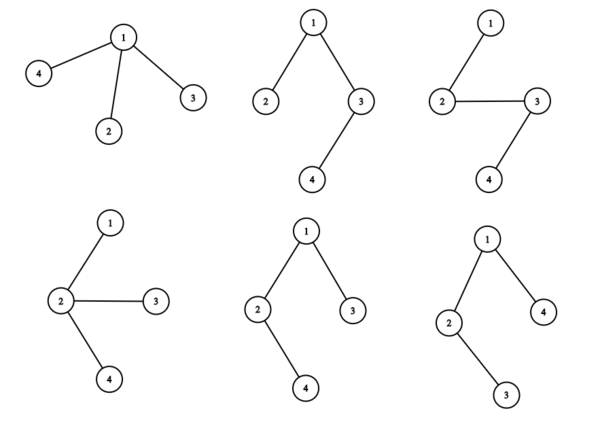
Вершина [math]1[/math] является корнем.
[math]P_{1,0} = 1[/math]
[math]P_{2,1} = 1\cdot P_{1,1}+(2-1)\cdot P_{1,0} = 1\cdot 0 + 1\cdot 1 = 1 [/math]
[math]P_{3,1} = 1\cdot P_{2,1}+(3-1))\cdot P_{2,0} = 1\cdot 1 + 2\cdot 0 = 1 [/math]
[math]P_{3,2} = 2\cdot P_{2,2}+(3-2))\cdot P_{2,1} = 2\cdot 0 + 1\cdot 1 = 1 [/math]
[math]P_{3,1} + P_{3,2} = 2[/math]
[math]P_{4,1} = 1\cdot P_{3,1}+(4-1))\cdot P_{3,0} = 1\cdot 1 + 3\cdot 0 = 1 [/math]
[math]P_{4,2} = 2\cdot P_{3,2}+(4-2))\cdot P_{3,1} = 2\cdot 1 + 2\cdot 1 = 4 [/math]
[math]P_{4,3} = 3\cdot P_{3,3}+(4-3))\cdot P_{3,2} = 3\cdot 0 + 1\cdot 1 = 1 [/math]
[math]P_{4,1} + P_{4,2} + P_{4,3}= 6[/math]
то есть получается, что это просто реккурента? А нет более интересных результатов, типа комбинаторного представления\производящей функции?