Обсуждение:Метод производящих функций — различия между версиями
Zevgeniy (обсуждение | вклад) м (UI) |
Zevgeniy (обсуждение | вклад) (progress...) |
||
| Строка 1: | Строка 1: | ||
| + | В комбинаторике, особенно в аналитической комбинаторике, символический метод - это метод подсчета комбинаторных объектов. Он использует внутреннюю структуру объектов для получения формул для их производящих функций. Этот метод в основном связан с Филиппом Флайоле и подробно описан в части а его книги с Робертом Седжвиком "аналитическая комбинаторика". Аналогичные языки для задания комбинаторных классов и их производящих функций найдены в работах Бендера и Гольдмана, Фоата и Шютценбергера, и Джойала. | ||
| + | |||
=Непомеченные комбинаторные объекты= | =Непомеченные комбинаторные объекты= | ||
| Строка 176: | Строка 178: | ||
=Помеченные объекты= | =Помеченные объекты= | ||
| + | |||
| + | Однако порой некоторые комбинаторные классы удобнее обозначать как помеченные. Например, — помеченные графы. С помеченными объектами используется экспоненциальная производящая функция. | ||
| + | |||
| + | Напомню, что если <tex dpi="350">\left \{ a_i \right \}</tex> {{---}} считающая последовательность, то производящие функции выражаются следующим образом: | ||
{| class="wikitable" | {| class="wikitable" | ||
| − | |||
|- | |- | ||
| − | | Обычная || <tex dpi="350">ogf(t) = \sum_{i=0}^{\infty}a_it^i</tex> | + | | Обычная || <tex dpi="350">ogf(t) = \sum_{i=0}^{\infty}a_it^i</tex> |
|- | |- | ||
| Экспоненциальная || <tex dpi="350">egf(t) = \sum_{i=0}^{\infty}\frac{a_it^i}{n!}</tex> | | Экспоненциальная || <tex dpi="350">egf(t) = \sum_{i=0}^{\infty}\frac{a_it^i}{n!}</tex> | ||
Версия 20:35, 24 июня 2020
В комбинаторике, особенно в аналитической комбинаторике, символический метод - это метод подсчета комбинаторных объектов. Он использует внутреннюю структуру объектов для получения формул для их производящих функций. Этот метод в основном связан с Филиппом Флайоле и подробно описан в части а его книги с Робертом Седжвиком "аналитическая комбинаторика". Аналогичные языки для задания комбинаторных классов и их производящих функций найдены в работах Бендера и Гольдмана, Фоата и Шютценбергера, и Джойала.
Непомеченные комбинаторные объекты
Каждый комбинаторный объект состоит из атомов.
У атомов определен вес .
| Определение: |
| Считающей последовательностью называется последовательность , где — количество объектов веса . |
Производящую функцию класса обозначим .
| Определение: |
| Комбинаторным объектом называется комбинаторный объект, состоящий из одного атома веса . |
Считающая последовательность: .
Производящая функция последовательности: .
| Определение: |
| Комбинаторным объектом называется комбинаторный объект, состоящий из одного атома веса . . |
Считающая последовательность: .
Производящая функция последовательности: .
| Определение: |
| Комбинаторным классом называется множество комбинаторных объектов, обладающих каким-то свойством. |
Объединение комбинаторных классов
| Определение: |
| Объединением комбинаторных классов и называется комбинаторный класс . |
При объединении комбинаторных классов одинаковые объекты разных классов считаются разными. Это делается так, чтобы не рассматривать внутреннюю структуру классов, а работать только со считающими последовательностями и производящими функциями.
Пары комбинаторных классов (декартово произведение комбинаторных классов)
| Определение: |
| Парой комбинаторных классов и называется комбинаторный класс . |
| Утверждение: |
| Верно, потому что коэффициенты производящей функции описываются равенством выше |
Последовательности комбинаторных классов
| Определение: |
| Последовательностью объектов из называется . |
| Утверждение: |
|
Докажем по индукции: База .
Переход.
|
| Определение: |
| Последовательностью (всех возможных длин) объектов из называется . |
| Утверждение: |
| (Геометрическая прогрессия) |
Ограничение: . Этому есть как техническое, так и комбинаторное объяснение.
- Технически, если , то мы будем делить на отрицательное число; если , то на функцию, у которой свободный член , — что формализм производящих функций сделать не позволяет.
- Комбинаторное объяснение заключается в том, что если объектов веса ноль более 0, то мы можем создать бесконечное количество последовательностей веса 0 (комбинируя такие объекты), а мы хотим работать с конечными количествами последовательностей.
Примеры
- Последовательночти из не менее 3 объектов:
- Последовательности чётной длины:
Комбинаторный объект "Натуральные числа"
Вес числа равен его значению. Каждое натуральное число встречается 1 раз.
Считающая последовательность:
— упорядоченное разбиение на слагаемые.
Множества
Множества — последовательности без повторений и порядка элементов.
Пример
Мультимножества
Мультимножества — последовательности с повторениями, но без порядка элементов.
Как и с существует ограничение на : .
Помеченные объекты
Однако порой некоторые комбинаторные классы удобнее обозначать как помеченные. Например, — помеченные графы. С помеченными объектами используется экспоненциальная производящая функция.
Напомню, что если — считающая последовательность, то производящие функции выражаются следующим образом:
| Обычная | |
| Экспоненциальная |
Свойства экспоненциальной производящей функции
| Утверждение: |
Пусть — экспоненциальная производящая функция последовательности , тогда — экспоненциальная производящая функция последовательности |
| Утверждение: |
Пусть — экспоненциальная производящая функция последовательности , тогда — экспоненциальная производящая функция последовательности |
| Утверждение: |
С точки зрения комбинаторики композиция производящих функций и означает подстановку вместо каждого возможного атома в всех объектов из класса .
|
Помеченные объекты
Помеченные комбинаторные объекты отличаются тем, что все атомы имеет разные значки, а именно — если вес объекта , то все атомы пронумерованы различными целыми числами от до .
Далее под производящей функцией будет подразумеваться экспоненциальная производящая функция.
| Определение: |
| Комбинаторным объектом называется комбинаторный объект, состоящий из одного атома веса . |
Производящая функция последовательности: .
| Определение: |
| Комбинаторным объектом называется комбинаторный объект, состоящий из одного атома веса . . |
Производящая функция последовательности: .
Объединение комбинаторных классов
Одинаковых объектов также нет, мы ставим разные метки на одинаковые объекты из разных классов, чтобы сделать их различными.
Пары комбинаторных классов (декартово произведение комбинаторных классов)
Напрямую декартово произведение нам не даст корректный комбинаторный объект.
Тогда пара ![]()
![]() будет иметь вес 5, но атомы не будут иметь различные пометки от 1 до 5.
будет иметь вес 5, но атомы не будут иметь различные пометки от 1 до 5.
Поэтому введем опреатор , который
- Перебирает все пары из и .
- В каждой паре перебирает все возможные способы перенумеровать атомы. Нумерация идёт в том же порядке, что и изначальная. То есть для каждого цикла при фиксированном наборе номеров есть ровно 1 способ занумеровать. Таким образом в классе будет
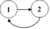
 , но не будет
, но не будет 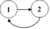
 .
.
(Сочетания)
Последовательности комбинаторных классов
Последовательности длины , как и в непомеченных комбинаторных объектах, формируются следующим образом:
- Мы составляем все возможные последовательности из объектов из
- Затем всеми возможными способами их перенумеруем.
Действует ограничение на как и и в в мире непомеченных объектов.
Обозначаются .
Определение и соответствующая производящая функция не изменились.
Пример
Перестановки
- Обычной производящей функции соответствует считающая последовательность , поэтому .
Урны
Урна характеризуется только количеством атомов в ней, поэтому
Множества
В помеченном мире , потому что не бывает одинаковых элементов в множествах.
— множество из k объектов (порядок не важен).
Каждому соответствует последовательностей в , потому что все объекты различны.
— множества объектов (порядок не важен).
Ограничение также действует.
— урна, где вместо атомов взяли объекты класса .