Подсчет деревьев — различия между версиями
Cuciev (обсуждение | вклад) (Image formatting fixed) |
(→Бинарные деревья) |
||
| Строка 4: | Строка 4: | ||
{{Утверждение | {{Утверждение | ||
|id=unmarked_bin | |id=unmarked_bin | ||
| − | |statement=Число непомеченных бинарных деревьев | + | |statement=Число непомеченных бинарных деревьев <tex>T_n</tex> равно <tex>C_{n}</tex> (<tex dpi="150">n</tex>-ое [[Числа Каталана|число Каталана]]). |
|proof= | |proof= | ||
Устройство бинарного дерева в терминах комбинаторных классов выражается следующим образом <tex>T = \varepsilon + z\times T\times T</tex>.<br> | Устройство бинарного дерева в терминах комбинаторных классов выражается следующим образом <tex>T = \varepsilon + z\times T\times T</tex>.<br> | ||
Версия 21:59, 20 августа 2020
Описание всех используемых далее комбинаторных объектов можно найти в статье "конструирование комбинаторных объектов и их подсчёт".
Непомеченные деревья
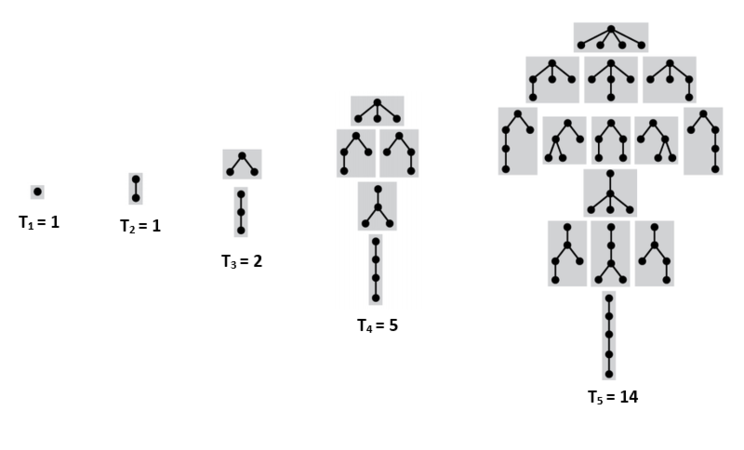
Бинарные деревья
| Утверждение: |
Число непомеченных бинарных деревьев равно (-ое число Каталана). |
|
Устройство бинарного дерева в терминах комбинаторных классов выражается следующим образом .
|
| Утверждение: |
Производящая функция числа непомеченных полных бинарных деревьев: . |
|
Устройство бинарного дерева в терминах комбинаторных классов выражается следующим образом . |
Подвешенные непомеченные деревьея с порядком на детях
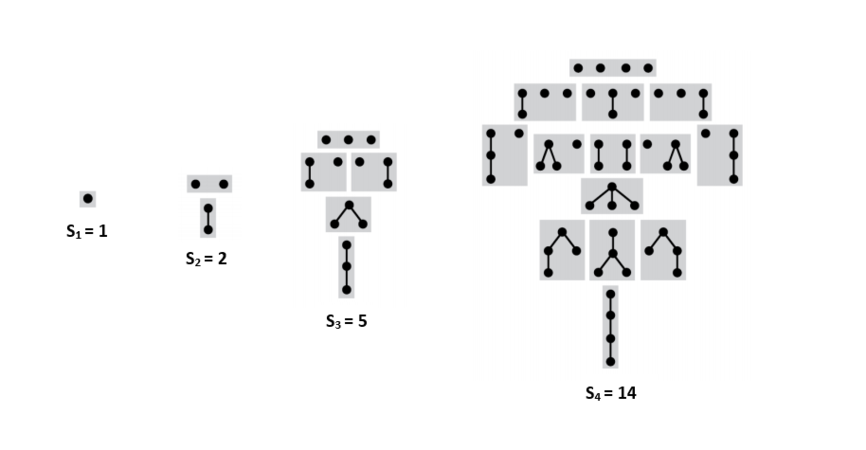
Пусть — количество таких деревьев с вершинами. — множество всех последовательностей из данных деревьев. — количество последовательностей с суммарным количество вершин . Чтобы получить дерево из вершин, достаточно взять вершину, и подвесить к ней последовательность деревьев с суммарным количеством вершин . Тогда:
- .
- , где — -ое число Каталана.
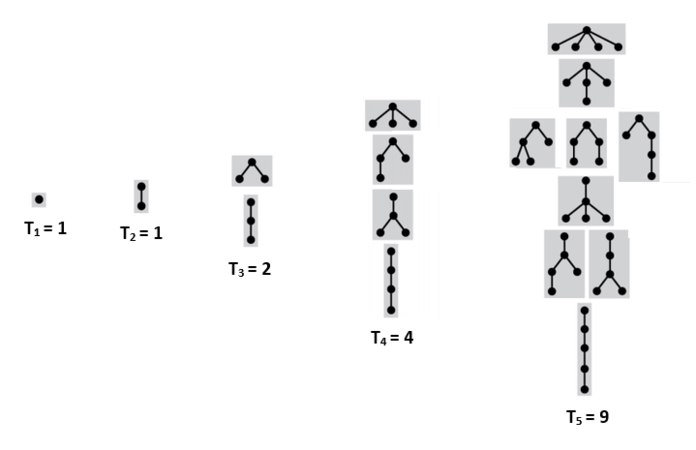
Подвешенные непомеченные деревья без порядка на детях
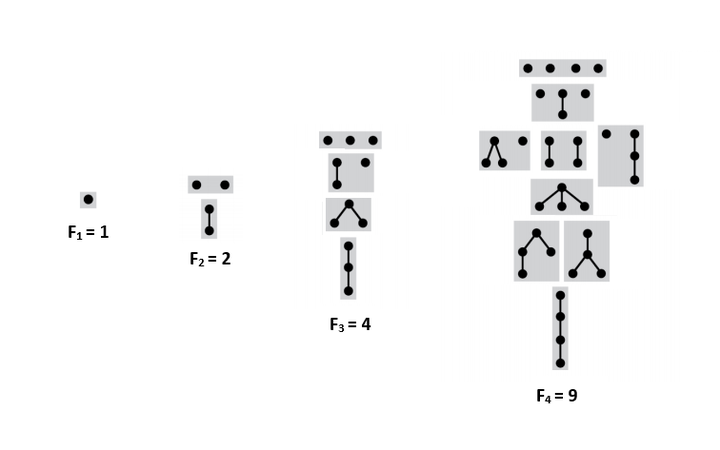
Пусть — количество таких деревьев с вершинами. — множество всех лесов из данных деревьев, так как лес можно интерпретировать как мультимножество из деревьев. — количество лесов с суммарным количество вершин . — количество таких лесов из вершин, что деревья в них содержат не более чем вершин. Чтобы получить дерево из вершин, достаточно взять вершину и подвесить к ней лес деревьев с суммарным количеством вершин . Тогда:
- .
- .
- .
Количество таких деревьев с вершинами образуют последовательность A000081[1].
Помеченные деревья
| Определение: |
| Помеченное дерево c вершинами - дерево c вершинами, вершинам которого взаимно однозначно соответствуют числа от 1 до n. |
| Теорема (Кэли): |
Число помеченных деревьев с вершинами равно . |
| Доказательство: |
|
Можно доказать формулу двумя способами. Первый способ.
Второй способ.
|
| Утверждение: |
Число помеченных корневых деревьев с вершинами есть . |
|
Данное утверждение является следствием теоремы Кэли. |
Подвешенные помеченные деревья с порядком на детях
| Утверждение: |
Число помеченных корневых деревьев с вершинами с порядком на детях есть . |
|
Как и в непомеченном случае, структура объекта остается неизменной: Производящая функция будет иметь вид: |
Подвешенные помеченные деревья без порядка на детях
| Утверждение: |
Как и в непомеченном случае, структура объекта остается неизменной: . Производящая функция будет иметь вид: |
Заметим, что в данной ситуации не получится простого соответствия, как в случае с деревьями с порядком на детях.
В случае порядка на детях не было нетривиальных автоморфизмов, порядок на детях однозначно задавал, как будут располагаться поддервевья.
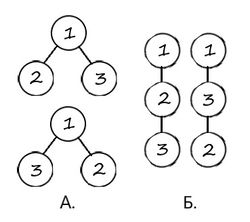
Если порядка на детях нет, ситуация становится сложнее:
В данном примере в А два представленных дерева — одинаковые, а в B — разные.
Для нет однозначно выражаемой формулы. Однако, можно получить, раскрыв экспоненту до -ого члена, а именно
Более подробное объяснение происходящего можно посмотреть в лекции[2].
См.также
- Конструирование комбинаторных объектов и их подсчёт
- Лемма Бёрнсайда и Теорема Пойа
- Числа Каталана
- Генерация комбинаторных объектов в лексикографическом порядке
Литература
- ↑ Number of unlabeled rooted trees with n node
- ↑ Станкевич А.С. Лекции по дискретной математике // Помеченные объекты и экспоненциальные ПФ, 2020. URL: https://youtu.be/6qQQj6G8-tA?t=4391