Участница:Наталья Юльцова

Преобразование регулярного выражения в ДКА

Алгоритм

1. Преобразуем регулярное выражение в ε-НКА.
2. Устраним ε-переходы.
3. Построим по НКА эквивалентное ДКА по алгоритму Томпсона.

Преобразование регулярного выражения в ε-НКА.

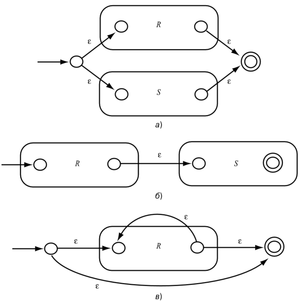
Рассмотрим подробнее как преобразуется регулярное выражение в ε-НКА. Автомат для выражения строится композицией из автоматов, соответствующих подвыражениям.

Виды выражений:

1. Данное выражение имеет вид R|S для некоторых подвыражений R и S. Тогда ему соответствует автомат, представленный на рис. a.
2. Выражение имеет вид RS. Автомат для этой конкатенации представлен на рис. b.
3. Выражение имеет вид R* для некоторого подвыражения R. Используем автомат, представленный на рис. c.

Пример

Преобразовать регулярное выражение (0|1)*1(0|1) в ДКА.

Регулярное выражение	Автомат
Преобразуем регулярное выражение [math](0|1)^*1(0|1)[/math] в ε-НКА. Построим сначала автомат для [math]0|1[/math]. Это выражение имеет вид 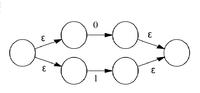[math]R|S[/math].
Далее считаем, что [math](0|1)[/math] это подвыражение вида R, и строим выражение 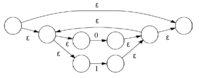[math](0|1)*[/math].
Выражение [math](0|1)*1[/math] имеет вид RS, [math](0|1)*1(0|1)[/math] имеет тот же вид.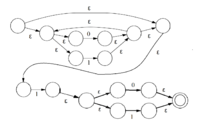
Удалим ε-переходы, согласно алгоритму из статьи, получим НКА.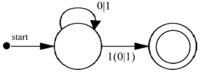
Преобразуем НКА в ДКА по алгоритму Томпсона и минимизируем ДКА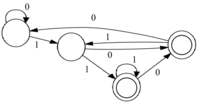

Преобразование ДКА в регулярное выражение

Алгебраический метод Бжозовского

Создадим систему регулярных выражений для каждого состояния в ДКА, а затем решим систему для регулярных выражений [math]R_i[/math], связанных с терминальным состояниями [math]q_i[/math]. Строим уравнения следующим образом: для каждого состояния [math]q_i[/math] уравнение [math]R_i[/math] является объединением переходов, ведущих в это состояние. Переход a из [math]q_i[/math] в [math]q_j[/math] обозначим за [math]aR_i[/math]. Если [math]q_i[/math] - терминальное состояние, то добавим в [math]R_i[/math] [math]\ne \varepsilon[/math]. Это приводит к системе уравнений вида:

[math] \begin{cases} R_1 = a_1*R_1 + a_2*R_2 + a_3*R_3 + ... \\ R_2 = a_1*R_1 + a_2*R_2 + a_3*R_3 + ... + \varepsilon \\ ... \\ R_m = a_1*R_1 + a_2*R_2 + a_3*R_3 + ... + \varepsilon \end{cases} [/math]

где [math]a_x[/math] = ∅ если нет перехода от [math]R_i[/math] к [math]R_j[/math]. Система может быть решена с помощью простой подстановки, за исключением случаев, когда неизвестное появляется как в правой, так и в левой части уравнения. Для этого воспользуемся теоремой Ардена:

Уравнение вида R = Q + RP, где P [math]\ne \varepsilon[/math], имеет решение R = QP*.

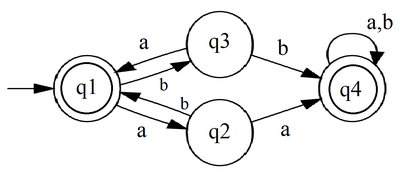
Пример

Найти: Регулярное выражение, удовлетворяющее данному ДКА.

Решение:

[math] \begin{cases} R_1 = b*R_2 + a*R_3 + \varepsilon \\ R_2 = a*R_1 \\ R_3 = b*R_1 \\ R_4 = a*R_2 + b*R_3 + a*R_4 + b*R_4 + \varepsilon \end{cases} [/math]

Рассмотрим первое терминальное состояние:

[math]R_1 = \varepsilon + abR_1 + baR_1 = \varepsilon + R_1(ab+ba)[/math]

Воспользуемся теоремой Ардена:

[math]R_1=(ab+ba)^*[/math]

Рассмотрим второе терминальное состояние :

[math]R_4=R_1(aa+bb)+R_4(a+b)=R_1(aa+bb)(a+b)^*[/math]

Объединим выражения для терминальных состояний и получим искомое регулярное выражение:

[math]R = R_1 + R_4= (ab+ba)^* (\varepsilon + (aa+bb) (a+b)^*)[/math]