Алгоритм Куна для поиска максимального паросочетания — различия между версиями
| Строка 1: | Строка 1: | ||
{{Теорема | {{Теорема | ||
|statement= | |statement= | ||
| − | Если из вершины <tex>x</tex> не существует дополняющей цепи относительно паросочетания <tex>M</tex>, то если паросочетание <tex>M'</tex> получается из <tex>M</tex> изменением вдоль дополняющей цепи, | + | Если из вершины <tex>x</tex> не существует дополняющей цепи относительно паросочетания <tex>M</tex>, то если паросочетание <tex>M'</tex> получается из <tex>M</tex> изменением вдоль дополняющей цепи, тогда из <tex>x</tex> не существует дополняющей цепи в <tex>M'</tex>. |
|proof= | |proof= | ||
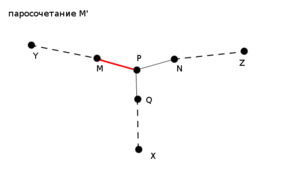
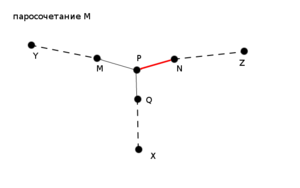
[[Файл:Kuhn1.png|thumb|left|300x300px|Пунктиром обозначен путь между двумя вершинами. Ребро красного цвета лежит в паросочетании, а черного - нет.]] | [[Файл:Kuhn1.png|thumb|left|300x300px|Пунктиром обозначен путь между двумя вершинами. Ребро красного цвета лежит в паросочетании, а черного - нет.]] | ||
Версия 22:44, 23 января 2011
| Теорема: |
Если из вершины не существует дополняющей цепи относительно паросочетания , то если паросочетание получается из изменением вдоль дополняющей цепи, тогда из не существует дополняющей цепи в . |
| Доказательство: |
|
Доказательство от противного. Допустим в паросочетание внесли изменения вдоль дополняющей цепи и из вершины появилась дополняющая цепь. Заметим, что эта дополняющая цепь должна вершинно пересекаться с той цепью, вдоль которой вносились изменения, иначе такая же дополняющая цепь из существовала и в исходном паросочетании. Пусть - ближайшая к вершина, которая принадлежит и новой дополняющей цепи и цепи . Тогда - последнее ребро на отрезке цепи , - последнее ребро на отрезке цепи , - последнее ребро лежащее на отрезке новой дополняющей цепи.(см. рисунок). Допустим принадлежит паросочетанию , тогда ему не принадлежит. Поскольку паросочетание получается из изменением вдоль дополняющей цепи , в паросочетание входило ребро , а ребро нет. Кроме того, ребро не лежит ни в исходном паросочетании , ни в паросочетании , в противном случае оказалось бы, что вершина инцидентна нескольким ребрам из паросочетания, что противоречит определению паросочетания. Тогда заметим, что цепь , полученная объединением цепей и , по определению будет дополняющей в паросочетании , что приводит к противоречию, поскольку в паросочетании из вершины не существует дополняющей цепи. |
Содержание
Алгоритм
Пусть дан двудольный граф и требуется найти максимальное паросочетание в нём. Обозначим доли исходного графа как и .
1) Просматриваем вершины из доли .
2) Будем искать дополняющую цепь из (например, поиском в глубину).
3) Если цепь найдена, инвертируем все ребра на этой цепи.
В любой момент времени текущим паросочетанием будет множество ребер, направленных из в . Корректность работы алгоритма следует из теоремы Бержа и доказанной выше теоремы.
Псевдокод
bool dfs(x): vis[x] = true for : k = py[y] if (k == -1) or ((not vis[k]) and (dfs(k))): py[y] = x return true return false Kuhn(): py[] = -1 for : vis[] = false dfs(s)
Время работы
Итак, алгоритм Куна можно представить как серию из || запусков обхода в глубину на всём графе. Следовательно, всего этот алгоритм исполняется за время , что в худшем случае есть .
Источники
Асанов М., Баранский В., Расин В. - Дискретная математика: Графы, матроиды, алгоритмы — СПб.: Издательство "Лань", 2010. — 291 стр.