Участница:Наталья Юльцова — различия между версиями
(→Преобразование регулярного выражения в НКА) |
(→Источники информации) |
||
| (не показана 21 промежуточная версия 2 участников) | |||
| Строка 9: | Строка 9: | ||
===Преобразование регулярного выражения в НКА=== | ===Преобразование регулярного выражения в НКА=== | ||
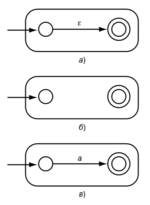
| − | [[Файл: | + | Преобразование проводится структурной индукцией по выражению <tex>R</tex>, следуя рекурсивному определению [[Регулярные языки: два определения и их эквивалентность| регулярных выражений]]. Необходимо рекурсивно "спуститься" вглубь языка <tex>L(R)</tex>, дойдя до нулевого уровня - <tex>R_0</tex>. Автоматы, распознающие <tex>L(R_0)</tex> представлены на рис. 1, это базис. |
| + | {| cellpadding="3" | ||
| + | |[[Файл:базис.png|150px|thumb|center|рис. 1. a. <tex>\varepsilon</tex> б. <tex>\varnothing</tex> в. <tex>a</tex>]] | ||
| + | |} | ||
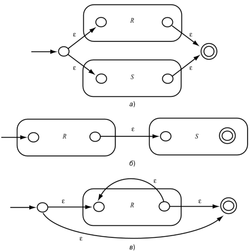
| + | Далее строится выражение <tex>\mathrm{R_{i+1}}</tex>, пока <tex>\mathrm{R_{i}} \ne R</tex> следующим образом: | ||
| − | + | # Выражение имеет вид <tex>R_i|S</tex>, для некоторых выражений <tex>R_i</tex> и <tex>S</tex>. Тогда ему соответствует автомат, представленный на рис. 2.a. Предполагаем, что <tex>R_i</tex> уже построено, а <tex>S</tex> строится по тому же алгоритму, что и <tex>R</tex>, значит, возможно построить <tex>\mathrm{R_{i+1}} = R_i|S</tex> | |
| + | # Выражение имеет вид <tex>R_iS</tex>. Автомат для этой конкатенации представлен на рис. 2.б. Предполагаем, что <tex>R_i</tex> уже построено, а <tex>S</tex> строится по тому же алгоритму, что и <tex>R</tex>, значит, возможно построить <tex>\mathrm{R_{i+1}} = R_iS</tex> | ||
| + | # Выражение имеет вид <tex>R_i^*</tex>. Используем автомат, представленный на рис. 2.в. | ||
| − | + | {| cellpadding="3" | |
| − | + | |[[Файл:RegToAut.png|250px|thumb|center|рис. 2. Индукционный переход преобразования регулярного выражения в НКА]] | |
| − | + | |} | |
===Пример=== | ===Пример=== | ||
| Строка 56: | Строка 62: | ||
</tex> | </tex> | ||
| − | где <tex>a_x</tex> = | + | где <tex>a_x</tex> = <tex>\varnothing</tex> если нет перехода от <tex>R_i</tex> к <tex>R_j</tex>. |
Система может быть решена с помощью простой подстановки, за исключением случаев, когда неизвестное появляется как в правой, так и в левой части уравнения. Для этого можно воспользоваться теоремой Ардена: | Система может быть решена с помощью простой подстановки, за исключением случаев, когда неизвестное появляется как в правой, так и в левой части уравнения. Для этого можно воспользоваться теоремой Ардена: | ||
| Строка 93: | Строка 99: | ||
<tex>R = R_1 + R_4= (ab+ba)^* (\varepsilon + (aa+bb) (a+b)^*)</tex> | <tex>R = R_1 + R_4= (ab+ba)^* (\varepsilon + (aa+bb) (a+b)^*)</tex> | ||
| − | |||
| − | |||
==Источники информации== | ==Источники информации== | ||
Текущая версия на 13:53, 8 января 2021
Содержание
Преобразование регулярного выражения в ДКА
Чтобы преобразовать регулярное выражение в ДКА, нужно:
- Преобразовать регулярное выражение в НКА с -переходами.
- Устранить -переходы.
- Построить по НКА эквивалентный ДКА.
Преобразование регулярного выражения в НКА
Преобразование проводится структурной индукцией по выражению , следуя рекурсивному определению регулярных выражений. Необходимо рекурсивно "спуститься" вглубь языка , дойдя до нулевого уровня - . Автоматы, распознающие представлены на рис. 1, это базис.
Далее строится выражение , пока следующим образом:
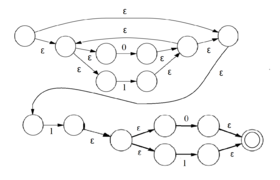
- Выражение имеет вид , для некоторых выражений и . Тогда ему соответствует автомат, представленный на рис. 2.a. Предполагаем, что уже построено, а строится по тому же алгоритму, что и , значит, возможно построить
- Выражение имеет вид . Автомат для этой конкатенации представлен на рис. 2.б. Предполагаем, что уже построено, а строится по тому же алгоритму, что и , значит, возможно построить
- Выражение имеет вид . Используем автомат, представленный на рис. 2.в.
Пример
Задача: Преобразовать регулярное выражение в ДКА.
| Регулярное выражение | Автомат |
|---|---|
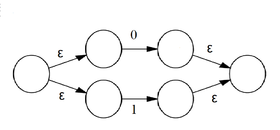
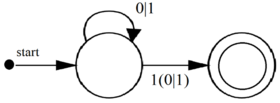
| Преобразуем регулярное выражение в -НКА. Построим сначала автомат для . Это выражение имеет вид . | |
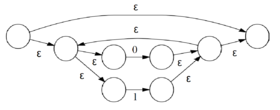
| Далее считаем, что это подвыражение вида , и строим выражение . | |
| Выражение имеет вид , имеет тот же вид. | |
| Удалим -переходы, согласно алгоритму из статьи, получим НКА. | |
| Преобразуем НКА в ДКА по алгоритму Томпсона. |
Преобразование ДКА в регулярное выражение
Алгебраический метод Бжозовского
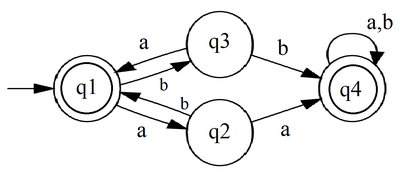
При преобразовании ДКА в регулярное выражение создается система регулярных выражений для каждого состояния в ДКА, а затем она решается для регулярных выражений , связанных с терминальным состояниями . Построение уравнения происходит следующим образом: для каждого состояния уравнение является объединением переходов, ведущих в это состояние. Переход a из в обозначается за . Если - терминальное состояние, то в добавляется . Это приводит к системе уравнений вида:
где = если нет перехода от к . Система может быть решена с помощью простой подстановки, за исключением случаев, когда неизвестное появляется как в правой, так и в левой части уравнения. Для этого можно воспользоваться теоремой Ардена:
Уравнение вида , где , имеет решение .
Пример
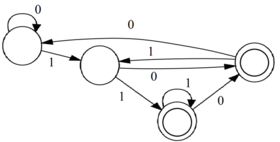
Задача: Построить регулярное выражение, удовлетворяющее данному ДКА.
Решение:
Рассмотрим первое терминальное состояние:
Воспользуемся теоремой Ардена:
Рассмотрим второе терминальное состояние :
Объединим выражения для терминальных состояний и получим искомое регулярное выражение:
Источники информации
- John E. Hopcroft, Rajeev Motwani, Jeffrey D. Ullman «Introduction to Automata Theory, Languages, and Computation», 2/E
- Christoph Neumann «Converting Deterministic Finite Automata to Regular Expressions»