Алгоритм Кока-Янгера-Касами разбора грамматики в НФХ — различия между версиями
(Новая страница: «Пусть дана грамматика <tex>\Gamma</tex> и слово <tex>w \in \Sigma^{*}</tex>. Требуется выяснить, выводится ли э…») |
(нет различий)
|
Версия 01:34, 23 февраля 2011
Пусть дана грамматика и слово . Требуется выяснить, выводится ли это слово в данной грамматике.
Алгоритм для НФХ-грамматики
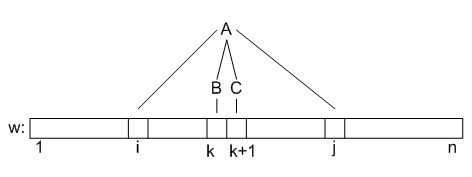
Пусть приведена к НФХ.
Представим , если можно из вывести подстроку . Иначе .
.
Базой динамики являются ячейки , которые заполняются истиной, если правило принадлежит грамматике:
.
Переход динамики имеет вид:
.
Пусть на текущем шаге . Тогда мы смотрим, можно ли вывести подстроку из ячеек матрицы, для которых и .
По окончанию динамики ответ будет содержаться в ячейке , где .
Сложность алгоритма
Необходимо вычислить булевских величин. На каждую требуется затратить операций, где – количество правил,. Суммируя по всем правилам получаем конечную сложность .
Алгоритму требуется памяти, где – количество нетерминалов грамматики.
Минус алгоритма заключается в том, что изначально грамматику необходимо привести к НФХ.