Дерево поиска, наивная реализация — различия между версиями
| Строка 20: | Строка 20: | ||
return Tree_search(x.right, k) | return Tree_search(x.right, k) | ||
Приведенная выше функция принимает в качестве параметров корень дерева и искомый ключ. Для каждого узла функция сравнивает значение его ключа с искомым ключом. Если ключи одинаковы, то функция возвращает текущий узел, в противном случае функция вызывается рекурсивно для левого или правого поддерева. Узлы, которые посещает функция образуют нисходящий путь от корня, так что время ее работы <tex>O(h)</tex>, где <tex>h</tex> - высота дерева. | Приведенная выше функция принимает в качестве параметров корень дерева и искомый ключ. Для каждого узла функция сравнивает значение его ключа с искомым ключом. Если ключи одинаковы, то функция возвращает текущий узел, в противном случае функция вызывается рекурсивно для левого или правого поддерева. Узлы, которые посещает функция образуют нисходящий путь от корня, так что время ее работы <tex>O(h)</tex>, где <tex>h</tex> - высота дерева. | ||
| − | поиск минимума и максимума | + | === поиск минимума и максимума === |
| − | поиск следующего и предыдущего элемента | + | Чтобы найти минимальный элемент в бинарном дереве поиска, необходимо просто следовать указателям left от корня дерева, пока не встретится значение hull. Если у вершины есть левое поддерево, то по свойству бинарного дерева поиска в нем хранятся все элементы с меньшим ключом. Если его нет, значит эта вершина и есть минимальная. Аналогично ищется и максимальный элемент. Для этого нужно следовать правым указателям. |
| − | вставка | + | Tree_min(root x) |
| − | удаление | + | while (x.left != null) |
| + | x = x.left | ||
| + | return x | ||
| + | |||
| + | Tree_max(root x) | ||
| + | while (x.right != null) | ||
| + | x = x.right | ||
| + | return x | ||
| + | Данные функции принимают корень дерева, и возвращают минимальный(максимальный) элемент в дереве. Обе процедуры выполняются за время <tex>O(h)</tex>. | ||
| + | === поиск следующего и предыдущего элемента === | ||
| + | === вставка === | ||
| + | === удаление === | ||
== Литература == | == Литература == | ||
1. Кормен, Т., Лейзерсон, Ч., Ривест, Р., Штайн, К. Алгоритмы: построение и анализ = Introduction to Algorithms / Под ред. И. В. Красикова. — 2-е изд. — М.: Вильямс, 2005. — 1296 с. — ISBN 5-8459-0857-4 | 1. Кормен, Т., Лейзерсон, Ч., Ривест, Р., Штайн, К. Алгоритмы: построение и анализ = Introduction to Algorithms / Под ред. И. В. Красикова. — 2-е изд. — М.: Вильямс, 2005. — 1296 с. — ISBN 5-8459-0857-4 | ||
Версия 00:40, 20 марта 2011
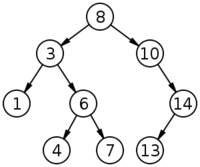
Бинарное дерево поиска должно обладать следующим свойством: Если x - узел бинарного дерева с ключом k, то все узлы в левом поддереве должны иметь ключи, меньшие k, а в правом поддереве большие k.
Содержание
Операции в бинарном дереве поиска
обход дерева поиска
Имеется простой алгоритм вывода всех ключей бинарного дерева поиска в отсортированном порядке.
Tree_walk(node x)
if(x != null)
Tree_walk(x.left);
print(x.key);
Tree_walt(x.right);
Данный алгоритм выполняет обход за время , поскольку процедура вызывается ровно два раза для каждого узла дерева. Корректность данного алгоритма следует из свойств бинарного дерева поиска.
поиск элемента
Для поиска элемента в бинарном дереве поиска можно воспользоваться следующей процедурой.
Tree_search(node x, key k)
if x == null or k == x.key
return x
if k < x.key
return Tree_search(x.left, k)
else
return Tree_search(x.right, k)
Приведенная выше функция принимает в качестве параметров корень дерева и искомый ключ. Для каждого узла функция сравнивает значение его ключа с искомым ключом. Если ключи одинаковы, то функция возвращает текущий узел, в противном случае функция вызывается рекурсивно для левого или правого поддерева. Узлы, которые посещает функция образуют нисходящий путь от корня, так что время ее работы , где - высота дерева.
поиск минимума и максимума
Чтобы найти минимальный элемент в бинарном дереве поиска, необходимо просто следовать указателям left от корня дерева, пока не встретится значение hull. Если у вершины есть левое поддерево, то по свойству бинарного дерева поиска в нем хранятся все элементы с меньшим ключом. Если его нет, значит эта вершина и есть минимальная. Аналогично ищется и максимальный элемент. Для этого нужно следовать правым указателям.
Tree_min(root x)
while (x.left != null)
x = x.left
return x
Tree_max(root x)
while (x.right != null)
x = x.right
return x
Данные функции принимают корень дерева, и возвращают минимальный(максимальный) элемент в дереве. Обе процедуры выполняются за время .
поиск следующего и предыдущего элемента
вставка
удаление
Литература
1. Кормен, Т., Лейзерсон, Ч., Ривест, Р., Штайн, К. Алгоритмы: построение и анализ = Introduction to Algorithms / Под ред. И. В. Красикова. — 2-е изд. — М.: Вильямс, 2005. — 1296 с. — ISBN 5-8459-0857-4