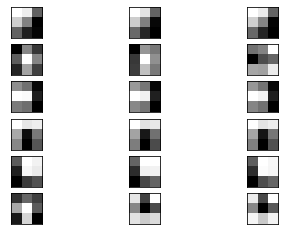Ядра — различия между версиями
Egormkn (обсуждение | вклад) (Оформлено определение) |
Leeloo (обсуждение | вклад) (Добавлен раздел Сверточные Ядра) |
||
| Строка 38: | Строка 38: | ||
* $K(\vec{x}_1, \vec{x}_2) = \sigma(\langle \vec{x}_1, \vec{x}_2 \rangle)$ — нейросеть с заданной функцией активации $\sigma(z)$ (не при всех $\sigma$ является ядром) | * $K(\vec{x}_1, \vec{x}_2) = \sigma(\langle \vec{x}_1, \vec{x}_2 \rangle)$ — нейросеть с заданной функцией активации $\sigma(z)$ (не при всех $\sigma$ является ядром) | ||
* $K(\vec{x}_1, \vec{x}_2) = \exp(-\beta \lVert \vec{x}_1 - \vec{x}_2 \rVert^2)$ — сеть радиальных базисных функций (англ. ''RBF'') | * $K(\vec{x}_1, \vec{x}_2) = \exp(-\beta \lVert \vec{x}_1 - \vec{x}_2 \rVert^2)$ — сеть радиальных базисных функций (англ. ''RBF'') | ||
| + | |||
| + | == Сверточные ядра == | ||
| + | |||
| + | [[Файл:vgg-16_block1_conv1_6_filters.png|upright=1.0|thumb|Рисунок 1. Визуализация первых 6 фильтров VGG-16 слоя block1_conv1, объединенные в триплеты. Некоторые из них имеют разные веса для разных каналов.]] | ||
| + | '''Сверточные ядра''' (англ. ''convolutional kernel'') — матрицы небольших размеров, с помощью которых производится [[Сверточные нейронные сети#Свертка|свертка]]. Используются для извлечения определенного признака, веса являются обучаемыми параметрами, например, с помощью градиентного спуска. Для разноцветных(с количеством каналов больше единицы) изображений используются фильтры, которые являются тензором ядер. Веса у таких ядер внутри тензора могут быть разного значения. Например, если в красной компоненте какой-то из признаков определяется сильнее, то веса будут больше чем в синей или зеленой компонентах. | ||
| + | |||
| + | |||
| + | === Примеры сверточных ядер === | ||
| + | |||
| + | ==== Определение границ ==== | ||
| + | |||
| + | '''Оператор Собеля''' (англ. ''Sobel operator'') — ядро размерности $3 \times 3$, которое вычисляет приближенное значение производной изображения. | ||
| + | |||
| + | * $G_x = \begin{bmatrix}1&0&-1\\2&0&2\\1&0&-1\end{bmatrix}$ горизонтальная компонента | ||
| + | * $G_y = \begin{bmatrix}1&2&1\\0&0&0\\-1&2&-1\end{bmatrix}$ вертикальная компонента | ||
| + | |||
| + | Горизонтальная и вертикальная компоненты могут быть скомбинированы для нахождения значения градиента в точке $G=\sqrt{G^2_x + G^2_y}$ | ||
| + | |||
| + | {|align="center" | ||
| + | |-valign="top" | ||
| + | |[[Файл:edge_detection_grayscale.jpg|200px|thumb|Рисунок 2. Оригинальное изображение в оттенках серого [https://upload.wikimedia.org/wikipedia/commons/thumb/3/3f/Bikesgray.jpg/200px-Bikesgray.jpg Источник]]] | ||
| + | |[[Файл:edge_detection_x.jpg|200px|thumb|Рисунок 3. Нормализованный градиент по координате х [https://en.wikipedia.org/wiki/File:Bikesgraygv.jpg Источник]]] | ||
| + | |[[Файл:edge_detection_y.jpg|200px|thumb|Рисунок 4. Нормализованный градиент по координате у [https://en.wikipedia.org/wiki/File:Bikesgraygh.jpg Источник]]] | ||
| + | |[[Файл:edge_detection_magnitude.jpg|200px|thumb|Рисунок 5. Нормализованный градиент исходного изображения [https://en.wikipedia.org/wiki/File:Bikesgraysobel.jpg Источник]]] | ||
| + | |} | ||
| + | |||
| + | ==== Определение линий ==== | ||
| + | |||
| + | Оператор определения линий с помощью сверточных ядер состоит из 4 матриц $3 \times 3$: горизонтальной, вертикальной, и двух наклонных($+45^{\circ}$ и $-45^{\circ}$) соответственно: | ||
| + | |||
| + | $\begin{bmatrix}-1&-1&-1\\2&2&2\\-1&-1&-1\end{bmatrix}$, $\begin{bmatrix}-1&2&-1\\-1&2&-1\\-1&2&-1\end{bmatrix}$, $\begin{bmatrix}-1&-1&2\\-1&2&-1\\2&-1&-1\end{bmatrix}$, $\begin{bmatrix}2&-1&-1\\-1&2&-1\\-1&-1&2\end{bmatrix}$ | ||
| + | |||
| + | {|align="center" | ||
| + | |-valign="top" | ||
| + | |[[Файл:line_detection_grayscale.gif|200px|thumb|Рисунок 6. Оригинальное изображение в оттенках серого [https://homepages.inf.ed.ac.uk/rbf/HIPR2/images/brg3.gif Источник]]] | ||
| + | |[[Файл:line_detection_after.gif|200px|thumb|Рисунок 7. изображение после применения оператора нахождения линий с нормализацией [https://homepages.inf.ed.ac.uk/rbf/HIPR2/images/brg3add2.gif Источник]]] | ||
| + | |} | ||
== См. также == | == См. также == | ||
* [[Метод опорных векторов (SVM)]] | * [[Метод опорных векторов (SVM)]] | ||
| + | * [[Сверточные нейронные сети]] | ||
== Примечания == | == Примечания == | ||
| Строка 48: | Строка 86: | ||
* [http://www.machinelearning.ru/wiki/index.php?title=%D0%9C%D0%B0%D1%88%D0%B8%D0%BD%D0%B0_%D0%BE%D0%BF%D0%BE%D1%80%D0%BD%D1%8B%D1%85_%D0%B2%D0%B5%D0%BA%D1%82%D0%BE%D1%80%D0%BE%D0%B2 machinelearning.ru — Машина опорных векторов] | * [http://www.machinelearning.ru/wiki/index.php?title=%D0%9C%D0%B0%D1%88%D0%B8%D0%BD%D0%B0_%D0%BE%D0%BF%D0%BE%D1%80%D0%BD%D1%8B%D1%85_%D0%B2%D0%B5%D0%BA%D1%82%D0%BE%D1%80%D0%BE%D0%B2 machinelearning.ru — Машина опорных векторов] | ||
* [https://www.youtube.com/watch?v=Adi67_94_gc&list=PLJOzdkh8T5kp99tGTEFjH_b9zqEQiiBtC&index=5 Лекция "Линейные методы классификации: метод опорных векторов"] — К.В. Воронцов, курс "Машинное обучение" 2014 | * [https://www.youtube.com/watch?v=Adi67_94_gc&list=PLJOzdkh8T5kp99tGTEFjH_b9zqEQiiBtC&index=5 Лекция "Линейные методы классификации: метод опорных векторов"] — К.В. Воронцов, курс "Машинное обучение" 2014 | ||
| + | * [https://homepages.inf.ed.ac.uk/rbf/HIPR2/linedet.htm HIPR Line Detection] | ||
| + | * [https://homepages.inf.ed.ac.uk/rbf/HIPR2/sobel.htm HIPR Sobel Edge Detector] | ||
[[Категория: Машинное обучение]] | [[Категория: Машинное обучение]] | ||
[[Категория: Классификация]] | [[Категория: Классификация]] | ||
[[Категория: Регрессия]] | [[Категория: Регрессия]] | ||
Версия 17:50, 21 января 2021
| Определение: |
| Ядро (англ. kernel) — функция $K: X \times X \to \mathbb{R}$, которая является скалярным произведением в некотором спрямляющем пространстве: $K(\vec{x}_1, \vec{x}_2) = \langle \psi(\vec{x}_1), \psi(\vec{x}_2) \rangle$ при некотором $\psi : X \to H$, где $H$ — пространство со скалярным произведением. |
Содержание
Выбор ядра
Теорема Мерсера определяет условия, при которых функция может являться ядром:
| Теорема (Мерсер): |
Функция $K(\vec{x}_1, \vec{x}_2)$ является ядром тогда и только тогда, когда выполнены условия: $\begin{cases}K(\vec{x}_1, \vec{x}_2) = K(\vec{x}_2, \vec{x}_1) & \text{(симметричность)} \\[1ex] \forall g: X \to \mathbb{R} \quad \int\limits_X \int\limits_X K(\vec{x}_1, \vec{x}_2) g(\vec{x}_1) g(\vec{x}_2) d \vec{x}_1 d \vec{x}_2 \geq 0 & \text{(неотрицательная определенность)}\end{cases}$ |
Проверка неотрицательной определённости является довольно трудоёмкой, поэтому на практике теорема явно не используется. Проблема выбора лучшего ядра на сегодняшний день остаётся открытой, лучшие из известных на данный момент решений основываются на генетических алгоритмах[1]). Обычно в практических реализациях ограничиваются перебором нескольких функций, про которые известно, что они являются ядрами, и выбирают среди них лучшую при помощи кросс-валидации. Кроме того, существуют правила порождения ядер, которые также применяются для расширения пространства перебираемых функций.
Конструктивные методы синтеза ядер
В целях достижения большей гибкости, и как следствие, более точных результатов, простые ядра могут быть объединены в более сложные функции, которые также будут являться ядром. Для этого используются следующие методы синтеза ядер:
- $K(\vec{x}_1, \vec{x}_2) = \langle \vec{x}_1, \vec{x}_2 \rangle \quad$ (скалярное произведение)
- $K(\vec{x}_1, \vec{x}_2) = \alpha \quad$ (константа $\alpha \in \mathbb{R}_+$)
- $K(\vec{x}_1, \vec{x}_2) = K_1(\vec{x}_1, \vec{x}_2) + K_2(\vec{x}_1, \vec{x}_2) \quad$ (сумма ядер)
- $K(\vec{x}_1, \vec{x}_2) = K_1(\vec{x}_1, \vec{x}_2) * K_2(\vec{x}_1, \vec{x}_2) \quad$ (произведение ядер)
- $K(\vec{x}_1, \vec{x}_2) = \psi(\vec{x}_1) * \psi(\vec{x}_2) \quad$ (произведение функций $\psi : X \to \mathbb{R}$)
- $K(\vec{x}_1, \vec{x}_2) = K_1(\phi(\vec{x}_1), \phi(\vec{x}_2)) \quad$ (композиция ядра и функции $\phi : X \to X$)
- $K(\vec{x}_1, \vec{x}_2) = \int\limits_X s(\vec{x}_1, \vec{z}) s(\vec{x}_2, \vec{z}) d \vec{z} \quad$ ($s : X \times X \to \mathbb{R}$ — симметричная интегрируемая функция)
- $K(\vec{x}_1, \vec{x}_2) = f(K_1(\vec{x}_1, \vec{x}_2)) \quad$ ($f: \mathbb{R} \to \mathbb{R}$ представима в виде сходящегося степенного ряда с неотрицательными коэффициентами)
Стандартные ядра
Существует несколько "стандартных" ядер, которые соответствуют известным алгоритмам классификации:
- $K(\vec{x}_1, \vec{x}_2) = (\langle \vec{x}_1, \vec{x}_2 \rangle + c)^d, \quad c, d \in \mathbb{R}$ — полиномиальное ядро
- $K(\vec{x}_1, \vec{x}_2) = \sigma(\langle \vec{x}_1, \vec{x}_2 \rangle)$ — нейросеть с заданной функцией активации $\sigma(z)$ (не при всех $\sigma$ является ядром)
- $K(\vec{x}_1, \vec{x}_2) = \exp(-\beta \lVert \vec{x}_1 - \vec{x}_2 \rVert^2)$ — сеть радиальных базисных функций (англ. RBF)
Сверточные ядра
Сверточные ядра (англ. convolutional kernel) — матрицы небольших размеров, с помощью которых производится свертка. Используются для извлечения определенного признака, веса являются обучаемыми параметрами, например, с помощью градиентного спуска. Для разноцветных(с количеством каналов больше единицы) изображений используются фильтры, которые являются тензором ядер. Веса у таких ядер внутри тензора могут быть разного значения. Например, если в красной компоненте какой-то из признаков определяется сильнее, то веса будут больше чем в синей или зеленой компонентах.
Примеры сверточных ядер
Определение границ
Оператор Собеля (англ. Sobel operator) — ядро размерности $3 \times 3$, которое вычисляет приближенное значение производной изображения.
- $G_x = \begin{bmatrix}1&0&-1\\2&0&2\\1&0&-1\end{bmatrix}$ горизонтальная компонента
- $G_y = \begin{bmatrix}1&2&1\\0&0&0\\-1&2&-1\end{bmatrix}$ вертикальная компонента
Горизонтальная и вертикальная компоненты могут быть скомбинированы для нахождения значения градиента в точке $G=\sqrt{G^2_x + G^2_y}$
 Рисунок 2. Оригинальное изображение в оттенках серого Источник |
 Рисунок 3. Нормализованный градиент по координате х Источник |
 Рисунок 4. Нормализованный градиент по координате у Источник |
 Рисунок 5. Нормализованный градиент исходного изображения Источник |
Определение линий
Оператор определения линий с помощью сверточных ядер состоит из 4 матриц $3 \times 3$: горизонтальной, вертикальной, и двух наклонных($+45^{\circ}$ и $-45^{\circ}$) соответственно:
$\begin{bmatrix}-1&-1&-1\\2&2&2\\-1&-1&-1\end{bmatrix}$, $\begin{bmatrix}-1&2&-1\\-1&2&-1\\-1&2&-1\end{bmatrix}$, $\begin{bmatrix}-1&-1&2\\-1&2&-1\\2&-1&-1\end{bmatrix}$, $\begin{bmatrix}2&-1&-1\\-1&2&-1\\-1&-1&2\end{bmatrix}$
 Рисунок 6. Оригинальное изображение в оттенках серого Источник |
 Рисунок 7. изображение после применения оператора нахождения линий с нормализацией Источник |
См. также
Примечания
Источники информации
- machinelearning.ru — Машина опорных векторов
- Лекция "Линейные методы классификации: метод опорных векторов" — К.В. Воронцов, курс "Машинное обучение" 2014
- HIPR Line Detection
- HIPR Sobel Edge Detector