Декомпозиция Эдмондса-Галлаи

В этом направлении много усилий приложили Вильям Томас Татт (William Thomas Tutte), Клод Берж (Claude Berge), Джек Эдмондс (Jack Edmonds) и Тибор Галлаи (Tibor Gallai).

Определение:

Дефицитом (англ. deficit) графа [math]G[/math] мы будем называть величину: [math]\mathrm{def}(G) = |V| - 2\alpha (G)[/math], где [math]\alpha (G)[/math] — размер максимального паросочетания в [math]G[/math], а [math]V(G)[/math] — множество вершин графа [math]G. [/math]

Определение:

[math]\mathrm{odd}({G})[/math] — число нечетных компонент связности в графе [math]{G}[/math], где нечетная компонента (англ. odd component) — это компонента связности, содержащая нечетное число вершин.

Лемма:

[math](n + |S| + odd(G \setminus S)) \; \equiv \; 0 \; ( mod \; 2) \; [/math], где [math]G[/math] — граф с [math]n[/math] вершинами, [math]S \in {V}_{G}[/math]

Доказательство:

[math]\triangleright[/math]

Удалим из графа [math]G[/math] множество [math]S[/math], получим [math]t[/math] компонент связности, содержащих [math]k_1, k_2 ... k_t[/math] вершин соответственно. [math]|S|\; + \; \sum_{i=1}^{k}k_i \; = \; n \; [/math], так как в сумме это все вершины исходного графа [math]G[/math]. Возьмем данное равенство по модулю два: [math](|S|\; + \; \sum_{i=1}^{k}k_i) \; \equiv \; n \; (mod \; 2)[/math] В сумме [math]\sum_{i=1}^{k}(k_i \; mod \; 2)[/math] число единиц равно числу нечетных компонент [math]odd(G \setminus S)[/math]. Таким образом, [math] \forall S \in V : \; (odd(G \setminus S) + |S|) \; \equiv \; n \; (mod \; 2) \;[/math].

[math]\triangleleft[/math]

Теорема (Бержа):

Для любого графа [math]G[/math] выполняется: [math]\mathrm{def}(G) = \max\limits_{S \subset V(G)} \{\mathrm{odd}(G - S) - |S|\}. [/math]

Доказательство:

[math]\triangleright[/math]

[math] \forall S \in V : \; (odd(G \setminus S) + |S|) \; \equiv \; n ( mod \; 2) \;[/math] Рассмотрим несколько случаев: 1. Если [math] \max\limits_{S \in V}(odd(G \setminus S) \; - \; |S|) \; = 0 \; [/math], тогда для любых [math]S \in V: \; odd(G \setminus S) \leq |S| \; [/math], следовательно выполнено условие теоремы Татта, значит, в графе есть совершенное паросочетание, то есть его дефицит равен нулю. 2. Если [math] \max\limits_{S \in V}(odd(G \setminus S) - |S|) = k \; [/math], тогда рассмотрим исходный граф [math]G[/math] и полный граф [math]K_k[/math] с [math]k[/math] вершинами, [math]W[/math] - вершины [math]K_k[/math]. Каждую вершину [math]K_k[/math] соединим с каждой вершиной [math]G[/math]. Получим граф [math]H \; = \; K_k + G \;[/math], докажем, что для него выполнено условие теоремы Татта. Докажем, что для любых [math]S \in V_{H}: odd(H \setminus S) \; \leq \; |S| \; [/math]. Рассмотрим [math]S \; \subset \; V_H\;[/math]: Если [math]W \not\subset S[/math], тогда поскольку граф [math]K_k[/math] полный и все его вершины связаны с каждой вершиной графа [math]G[/math], то граф [math]H[/math] связный и [math]odd(H \setminus S) \; = \; 0 \;[/math] или [math]odd(G \setminus S) \; = \; 1 \;[/math]. В случае [math]odd(H \setminus S) \; = \; 0 \; [/math] условие очевидно выполняется, так как для любых [math]S \in G : 0 \; \leq \; |S| \;[/math]. Рассмотрим случай [math]odd(H \setminus S) \; = \; 1 \;[/math], [math]|V_H| \; = \; n \; + \; k \; = \; n \; + \; odd(G \setminus A) \; - \; |A| \; [/math], где [math]A \; = \; arg \max\limits_{S \in V}(odd(G \setminus S) \; - \; |S|) \; [/math]. Разность [math]odd(G \setminus A) \; - \; |A| \; [/math] имеет ту же четность, что и [math]n[/math], и [math]odd(H \setminus S) \; = \; 1 \;[/math], поэтому [math]|V_H|[/math] четно, значит, по лемме, мощность [math]S[/math] нечетна, следовательно она не равна нулю, значит, [math] 1 \leq |S| [/math]. Если [math]W \subset S \;[/math], то [math]odd(H \setminus S) \; = \; odd(G \setminus (S \cap V)) \; = odd(G \setminus (S \cap V)) \; - \; |S \cap V| \; + \; |S \cap V| \; \leq \; |S \cap V| \; + \; k \leq |S| \; [/math], так как [math] \max\limits_{S \in V}(odd(G \setminus S) - |S|) = k \; [/math]. Таким образом, для графа [math]H[/math] выполнено условие теоремы Татта, следовательно в нём есть полное паросочетание. Рассмотрим полное паросочетание в графе [math]H[/math], удалим вершины [math]W[/math] из графа [math]H[/math]. Количество непокрытых вершин после удаления не больше, чем количество удаленных вершин [math]k[/math], значит, [math]def(G) \; \leq \; k[/math]. Удалим множество вершин [math]A \; = \; arg \max\limits_{S \in V}(odd(H \setminus S) \; - \; |S|) \; [/math] из графа [math]G\;[/math]. Заметим, что после удаления в графе осталось [math]odd(G \setminus A)\; [/math] нечетных компонент и образовались новые непокрытые вершины, но при этом число нечетных компонент больше числа удаленных на [math]k[/math]. Значит, хотя бы [math]k[/math] нечетных компонент содержали исходно непокрытую вершину, следовательно [math]def(G) \; \geq \; k \; [/math]. Из [math]def(G) \; \leq \; k[/math] и [math]def(G) \; \geq \; k \; [/math] следует [math]def(G) \; = \; k \; [/math].

[math]\triangleleft[/math]

Теорема (Татта-Бержа):

Дан граф [math]G[/math], размер максимального паросочетания в нем равен: [math]\mathrm{\alpha}(G) = \min\limits_{U \in V} \{\dfrac{1}{2}(|V|+|U|-\mathrm{odd}(G - U)\}. [/math]

Доказательство:

[math]\triangleright[/math]

Предположим [math]G[/math] — связный, иначе мы можем применить индукцию к компонентам [math]G[/math]. Приведем доказательство по индукции по числу вершин в графе. База индукции: Очевидно, для [math] n = 1 [/math] утверждение верно. Индукционный переход: Рассмотрим два случая: [math]G[/math] — содержит вершину [math]v[/math] покрытую всеми максимальными паросочетаниями (например средняя вершина) Тогда [math] \mathrm{\alpha}(G - v) = \mathrm{\alpha}(G) - 1 [/math]. По индукции, формула Татта-Берджа содержит [math]G - v[/math] для некоторого множества [math]U'[/math]. Пусть [math]U = U' \bigcup v[/math]. Тогда: [math] \mathrm{\alpha}(G) = \mathrm{\alpha}(G - v) + 1 = \dfrac{1}{2}(|V - v|+|U - v| - \mathrm{odd}(G - v - (U - v))) + 1 = [/math] [math] = \dfrac{1}{2}(|V| - 1 + |U|- 1 - \mathrm{odd}(G - U)) + 1 = \dfrac{1}{2}(|V|+|U| - \mathrm{odd}(G - U)). [/math] Для каждой вершины [math]v[/math] есть максимальное паросочетание [math]M[/math] которое не покрывает [math]v[/math] (например [math]C_3[/math]) Покажем, что существует паросочетание размера [math] \dfrac{1}{2}(|V| - 1) [/math], из которого следует теорема (при [math] U = \emptyset [/math]). От противного: Предположим что любое максимальная паросочетание [math] M [/math] не покрывает, по крайней мере, две различные вершины [math] u [/math] и [math] v [/math]. Среди всех таких [math] (M, u, v) [/math] выберем их так, что [math] \mathrm{d}(u, u) [/math] в [math] G [/math] — минимально. Если [math] \mathrm{d}(u, u) = 1 [/math], то [math] u [/math] и [math] v [/math] являются смежными, и, следовательно, мы можем увеличить [math] M [/math], что противоречит его максимальности. Значит [math] \mathrm{d}(u, u) \geqslant 2 [/math], и, следовательно, мы можем выбрать промежуточную вершину [math] t [/math] на пути [math] u-v [/math] и [math] N [/math] максимальное паросочетание, такое что симметрическая разность с [math] M [/math] минимальна. Так как [math] (M, u, v) [/math] минимально, то [math] N [/math] должно охватывать [math] u [/math] и [math] v [/math] так, что есть другая вершина [math] x [/math], покрытая только в [math] M [/math]. Пусть [math] y [/math] будет вершиной покрытой с [math] x [/math] в [math] M [/math] и заметим [math] y \neq t [/math] (иначе можно было бы добавить к [math] N [/math]). Пусть [math] z [/math] будет вершиной покрытой с [math] y [/math] в [math] N [/math] и заметим [math] z \neq x [/math] (так как [math] x [/math] не покрыто в [math] N [/math]). Тогда [math] N - yz + xy [/math] — паросочетание, которое имеет с [math] M [/math] меньшую симметрическую разность, что противоречит выбору [math] N [/math].

[math]\triangleleft[/math]

Определение:

Множество [math]S \subset V (G)[/math], для которого [math]\mathrm{odd}(G - S) - |S| = \mathrm{def}(G) [/math], называется барьером (англ. barrier).

Определение:

Пусть [math]X \subset V [/math]. Множeство соседей (англ. neighbors) [math]X[/math] определим формулой: [math]N(X)= \{ y \in V:(x,y) \in E \}[/math]

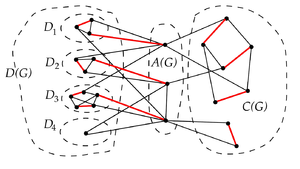
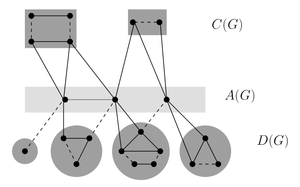
Структурная теорема Эдмондса-Галлаи

Определение:

Структурные единицы декопозиции:

1. [math]D(G) = \{v \in V \mid [/math] существует максимальное паросочетание, не покрывающее [math] v\}[/math]
2. [math]A(G) = N(D(G)) \setminus D(G)[/math]
3. [math]C(G) = V \setminus(D(G) \bigcup A(G))[/math]
4. [math] \alpha (G) [/math] — размер максимального паросочетания в [math] G. [/math]

Пример. Рёбра из паросочетания выделены красным

Определение:

Граф [math]G[/math] называется фактор-критическим (англ. factor-critical graph), если для любой вершины [math]v \in G[/math] в графе [math]G \setminus {v}[/math] существует совершенное паросочетание.

Теорема (Галлаи):

[math]G[/math] — фактор-критический граф [math] \Leftrightarrow [/math] [math]G[/math] — связен и для любой вершины [math]u \in V(G) [/math] выполняется равенство [math] \alpha (G - u) = \alpha (G)[/math].

Лемма (Галлаи, о стабильности (англ. stability lemma)):

Пусть [math] a \in A(G).[/math] Тогда: [math]D(G - a) = D(G)[/math] [math]A(G - a) = A(G) \setminus \{a\}[/math] [math]C(G - a) = C(G)[/math] [math] \alpha (G - a) = \alpha (G) - 1.[/math]

Доказательство:

[math]\triangleright[/math]

Для начала докажем, что [math]D(G - a) = D(G)[/math]. Случай а Случай b Случай c Покажем, что [math]D(G - a) \supset D(G)[/math] : Пусть [math]u \in D(G)[/math]. Тогда существует максимальное паросочетание [math]M_u[/math] графа [math]G[/math], не покрывающее [math]u[/math]. Поскольку любое максимальное паросочетание графа [math]G[/math] покрывает [math]a[/math], то [math] \alpha (G - a) = \alpha (G) - 1 [/math] и более того, если, для некоторой вершины [math]x \in D(G)[/math], [math]ax \in M_u[/math], то [math]M_u \setminus {ax} [/math] — максимальное паросочетание графа [math] G - a [/math], не покрывающее [math] u [/math]. Таким образом, [math]D(G - a) \supset D(G) [/math]. покажем, что [math] D(G - a) \subset D(G)[/math]: Предположим, что существует максимальное паросочетание [math]M'[/math] графа [math] G - a[/math], не покрывающее вершину [math]v[/math] [math] \notin D(G)[/math]. Пусть [math] w \in D(G) [/math] — смежная с [math] a \in A(G)[/math] вершина, а [math] M_w [/math] — максимальное паросочетание графа [math] G [/math], не покрывающее [math] w [/math]. Так как [math]v[/math] [math] \notin D(G) [/math], максимальное паросочетание [math] M_w [/math] покрывает вершину [math]v[/math]. Рассмотрим граф [math] H = G(M_w \bigcup M') [/math] — очевидно, он является объединением нескольких путей и чётных циклов. Пусть [math] U [/math] — компонента связности графа [math] H [/math], содержащая [math]v[/math]. Так как [math] deg_H(v) = 1 [/math] (степень вершины), то [math] P = H(U) [/math] — путь с началом в вершине [math]v[/math]. В пути [math]P[/math] чередуются рёбра из [math] M_w[/math] и [math]M' [/math], причём начинается путь ребром из [math]M_w [/math]. Так как [math] deg_H(a) = 1 [/math], то вершина a либо не принадлежит пути [math]P[/math], либо является её концом (в этом случае последнее ребро пути принадлежит паросочетанию [math] M_w[/math]). Рассмотрим несколько случаев: a. Путь [math]P[/math] кончается ребром из [math] M'[/math] (см. рисунок) Рассмотрим паросочетание [math]M_v = M_w \oplus E(P)[/math] (симметрическая разность [math] M_w[/math] и [math]E(P)[/math]. то есть, рёбра, входящие ровно в одно из двух множеств). Очевидно, [math]M_v[/math] — максимальное паросочетание графа [math]G[/math], не покрывающее [math]v[/math], поэтому [math] v \in D(G)[/math], противоречие. b. Путь [math]P[/math] кончается ребром из [math] M_w[/math], вершина [math]a[/math] — конец пути [math]P[/math]. (см.рисунок) Рассмотрим паросочетание [math]M_v∗ = (M_w \oplus E(P)) \bigcup \{aw\} [/math]. Тогда [math] M_v∗ [/math] — максимальное паросочетание графа [math] G [/math], не покрывающее [math] v [/math], поэтому [math] v \in D(G) [/math], противоречие. c. Путь [math] P [/math] кончается ребром из [math] M_w, a \in V(P) [/math] (см. рисунок) Рассмотрим паросочетание [math] M'' = M \oplus E(P) [/math]. Тогда [math] |M''| = |M'| + 1 [/math], причём [math]M'' \subset E(G - a)[/math]. Противоречие с максимальностью паросочетания [math]M'[/math]. Таким образом, наше предположение невозможно и [math]D(G - a) \subset D(G)[/math]. А значит, [math]D(G - a) = D(G)[/math]. Так как [math]D(G - a) = D(G)[/math], то все вершины, которые были соседями [math]D(G)[/math], таковыми и остались. Однако, по условию [math] a \in A(G)[/math], значит [math]A(G - a) = A(G) \setminus \{a\}[/math]. Так же заметим, что [math]C(G - a) = V(G - a) \setminus (D(G - a) \cup A(G - a)) = V(G - a) \setminus (D(G) \cup (A(G) \setminus \{a\}))[/math][math] = V(G) \setminus (D(G) \cup A(G)) = C(G)[/math] Наконец, так как [math] a \in A(G)[/math], то все максимальные паросочетания в [math]G[/math] включали [math]a[/math]. Следовательно, [math]\alpha (G - a) \lt \alpha (G)[/math]. Заметим, что, взяв любое максимальное паросочетания в [math]G[/math] и удалив ребро инцидентное [math]a[/math], мы получим паросочетание [math]M'[/math], которое на 1 меньше исходного, при этом [math]M' \in E(G - a)[/math]. В свою очередь, это самое большое паросочетание, которое мы могли теоретически получить в [math]G - a[/math]. Следовательно, [math] \alpha (G - a) = \alpha (G) - 1.[/math]

[math]\triangleleft[/math]

Теорема (Галлаи, Эдмондс):

Пусть [math]G[/math] — граф, [math]U_1\ldots U_n[/math] — компоненты связности графа [math]G(D(G))[/math], [math]D_i = G(U_i), C = G(C(G))[/math]. Тогда: Граф [math]C[/math] имеет совершенное паросочетание. Графы [math]D_1\ldots D_n[/math] — фактор-критические. Любое максимальное паросочетание [math]M[/math] графа [math] G [/math] состоит из совершенного паросочетания графа [math] C [/math], почти совершенных паросочетаний графов [math] D_1\ldots D_n [/math] и покрывает все вершины множества [math] A(G) [/math] рёбрами с концами в различных компонентах связности [math] U_1\ldots U_n. [/math] [math]\mathrm{def}(G) = n - |A(G)|.[/math] [math]2\mathrm{\alpha}(G) = v(G) + |A(G)| - n[/math].

Доказательство:

[math]\triangleright[/math]

Пример Последовательно удаляя вершины множества [math]A = A(G)[/math], по лемме о стабильности мы получим: [math]D(G - A) = D(G),[/math] [math]A(G - A) = \O, [/math] [math]C(G - A) = C(G),[/math] [math]\alpha (G - A) = \alpha (G) - |A|.[/math] Это означает, что не существует рёбер, соединяющих вершины из [math]C(G - A)[/math] и [math]D(G - A)[/math]. Каждое максимальное паросочетание [math]M'[/math] графа [math]G - A[/math] покрывает все вершины множества [math]C(G)[/math], поэтому [math]M'[/math] содержит совершенное паросочетание графа [math]C[/math]. Тем самым, мы доказали пункт [math]1)[/math]. Из формулы [math] \alpha(G - A) = \alpha (G) - |A|[/math] следует, что [math]U_1\ldots U_n[/math] — компоненты связности графа [math]G - A[/math]. Для любой вершины [math]u \in U_i[/math] существует максимальное паросочетание [math]M_u[/math] графа [math]G - A[/math], не содержащее [math]u[/math]. Так как [math]U_i[/math] — компонента связности графа [math]G - A[/math], паросочетание [math]M_u[/math] содержит максимальное паросочетание графа [math]D_i[/math] (разумеется, не покрывающее вершину [math]u[/math]). Следовательно, [math] \alpha (D_i) = \alpha (D_i - u) [/math] и по теореме Галлаи (мы получаем, что граф [math]D_i[/math] — фактор-критический. Пусть [math]M[/math] — максимальное паросочетание графа [math]G[/math], а [math]M'[/math] получено из [math]M[/math] удалением всех рёбер, инцидентных вершинам множества [math]A[/math]. Тогда [math]|M'| \geqslant |M| - |A|[/math] и по формуле [math] \alpha (G - A) = \alpha (G) - |A|[/math] понятно, что [math]M'[/math] — максимальное паросочетание графа [math]G - A[/math]. Более того, из [math] \alpha (G - A) = \alpha (G) - |A|[/math] следует [math]|M'| = |M| - |A|[/math], а значит, все вершины множества [math]A[/math] покрыты в [math]M[/math] различными рёбрами. Так как [math]M'[/math] — максимальное паросочетание графа [math]G - A[/math], то по пунктам [math]1)[/math] и [math]2)[/math] очевидно, что [math]M'[/math] содержит совершенное паросочетание графа [math]C[/math] и почти совершенные паросочетания фактор-критических графов [math]D_1\ldots D_n[/math]. Значит, рёбра паросочетания [math]M[/math] соединяют вершины [math]A[/math] с непокрытыми [math]M'[/math] вершинами различных компонент связности из [math]U_1\ldots U_n[/math]. Из пункта [math]3)[/math] сразу же следуют равенства пункта [math]4)[/math] и [math]5)[/math].

[math]\triangleleft[/math]

Утверждение (следствие из теоремы):

[math]A(G)[/math] — барьер графа [math]G[/math]

Лемма (о связи барьера с [math]D(G)[/math]):

Для любого барьера [math]B[/math] графа [math]G[/math] верно, что [math]B\cap D(G) = \varnothing[/math]

Доказательство:

[math]\triangleright[/math]

Рассмотрим [math]U_{1}, U_{2}, \ldots U_{n}[/math] — нечётные компоненты связанности [math]G \setminus B[/math], [math]\ M[/math] — максимальное паросочетание в [math]G[/math]. [math]\forall\ U_{i}\ \exists x \in U_{i}: x[/math] не покрыта [math]\ M[/math] или [math]xv \in M \land v \in B[/math]. Всего графе не покрыто хотя бы [math]odd(G\setminus B) - |B|[/math] вершин. Однако, так как [math]B[/math] — барьер, непокрыто ровно столько вершин. Следовательно, любое максимальное паросочетание не покрывает только вершины из [math]G \setminus B[/math], а значит каждая вершина барьера покрыта в любом максимальном паросочетании. Отсюда получаем, что ни одна вершина из [math]D(G)[/math] не могла оказаться в барьере.

[math]\triangleleft[/math]

Утверждение (Следствие из леммы):

В любом максимальном паросочетании все вершины барьера соединены соединены с вершинами [math]G \setminus B[/math]

[math]\triangleright[/math]

Так как для барьера [math]B[/math] верно, что [math]odd(G\setminus B) - |B|=def(G) \geqslant 0[/math], то ровно [math]|B|[/math] вершин из нечётных компонент [math]G \setminus B[/math] покрыты рёбрами [math]xv \in M \land v \in B[/math]

[math]\triangleleft[/math]

Лемма (о дополнении барьера):

Пусть [math]x\in A(G)\cup C(G),\ G'=G\setminus x,\ B'[/math] — барьер графа [math]G'[/math]. Тогда [math]B=B'\cup x[/math] — барьер графа [math]G[/math]

Доказательство:

[math]\triangleright[/math]

Так как [math]x \notin D(G)[/math], то для любого максимального паросочетания [math]M: x \in M[/math]. Следовательно, [math]|M'| = |M| - 1[/math], где [math]M'[/math] — максимальное паросочетание в [math]G'[/math]. [math]def(G') = (|V| - 1)- 2 \cdot |M'| = |V| - 2 \cdot |M| + 1 = def(G) + 1[/math] [math]odd(G - (B'\cup x)) = odd(G' - B') = [/math][math]|B'| + def(G') = |B'| + 1 + def(G) = |B'\cup x| + def(G)[/math] Отсюда следует, что [math]B[/math] — барьер графа [math]G[/math].

[math]\triangleleft[/math]

Теорема (о структуре барьера):

Любой барьер графа состоит только из вершин [math]A(G)\cup C(G)[/math], причём каждая вершина из этого множества входит в какой-то барьер

Доказательство:

[math]\triangleright[/math]

По лемме о связи барьера с [math]D(G)[/math] мы знаем, что в барьере нет вершин вершин из [math]D(G)[/math]. По лемме о дополнение барьера мы можем взять любую вершину из [math]A(G)\cup C(G)[/math], удалить из графа, и с помощью барьера нового графа получить барьер исходного, включающий данную вершину.

[math]\triangleleft[/math]

См. также

• Теорема Татта о существовании полного паросочетания
• Лапы и минимальные по включению барьеры в графе
• Пересечение всех максимальных по включению барьеров

Источники информации

• Edmonds-Gallai Decomposition and Factor-Critical Graphs
• Edmonds-Gallai Decomposition, Edmonds’ Algorithm
• — Лекция А.С. Станкевича