Реляционная алгебра: унарные операции — различия между версиями
Dzhiblavi (обсуждение | вклад) м |
(Добавлен текст) |
||
| Строка 1: | Строка 1: | ||
| − | В этом разделе будут описаны унарные операции в рамках [[Реляционная_алгебра|реляционной алгебры]]. В соответствии с определением, для каждой операции | + | В этом разделе будут описаны унарные операции в рамках [[Реляционная_алгебра|реляционной алгебры]]. В соответствии с определением, для определения каждой операции нужно указать способ построения заголовка, тела отношения, а также условия применимости, если такие есть. |
== Проекция == | == Проекция == | ||
| Строка 10: | Строка 10: | ||
}} | }} | ||
| − | + | Данная операция полезна как минимум для следующего: | |
| + | * Привести отношение к виду, в котором с ним можно будет осуществить другую операцию (например, объединение); | ||
| + | * Выбрать из отношения только нужные данные (для выборки). | ||
| + | |||
| + | Ниже приведено пояснение определения для операции <tex>\pi_{A_2, A_4, A_5}(A)</tex>: | ||
[[Файл:Primitive_Projection_0.png]] | [[Файл:Primitive_Projection_0.png]] | ||
| + | |||
| + | Синим обозначены столбцы, которые есть в результирующем отношении. Остальные столбцы не используются, и результат не зависит от данных, которые там находятся. | ||
'''Примеры''' | '''Примеры''' | ||
| + | |||
| + | Приведем несколько тривиальных примеров применения проекции. | ||
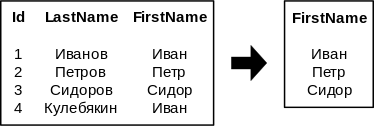
* <tex>\pi_{FirstName, LastName}</tex> | * <tex>\pi_{FirstName, LastName}</tex> | ||
| Строка 31: | Строка 39: | ||
}} | }} | ||
| − | + | Данная операция крайне часто используется для | |
| + | * Ограничения области действия изменяющих запросов; | ||
| + | * Получения выборки данных, соответствующих определенному условию. | ||
| + | |||
[[Файл:Primitive_Section_0.png]] | [[Файл:Primitive_Section_0.png]] | ||
'''Примеры''' | '''Примеры''' | ||
| + | |||
| + | Приведем несколько тривиальных примеров применения фильтрации. | ||
| + | |||
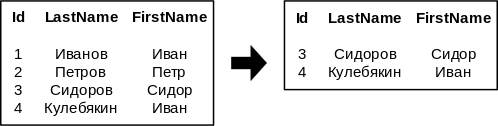
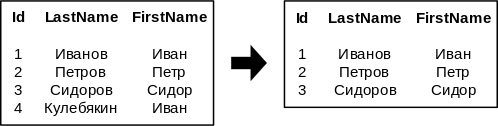
* <tex>\sigma_{Id > 2}</tex> | * <tex>\sigma_{Id > 2}</tex> | ||
[[Файл:Primitive_Section_2.png]] | [[Файл:Primitive_Section_2.png]] | ||
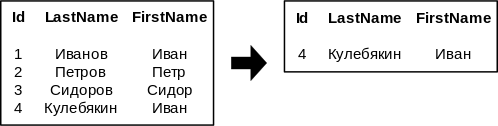
| − | * <tex>\sigma_{Id > 2 \wedge FirstName=Иван}</tex> | + | * Можно писать и более сложные условия: <tex>\sigma_{Id > 2 \wedge FirstName=Иван}</tex> |
[[Файл:Primitive_Section_3.png]] | [[Файл:Primitive_Section_3.png]] | ||
| − | * <tex>\sigma_{length(FirstName) + 2 \geq length(LastName)}</tex> | + | * Еще можно исопльзовать функции, доступные в БД: <tex>\sigma_{length(FirstName) + 2 \geq length(LastName)}</tex> |
[[Файл:Primitive_Section_4.png]] | [[Файл:Primitive_Section_4.png]] | ||
| Строка 55: | Строка 69: | ||
}} | }} | ||
| + | Операция часто применяется для того, чтобы отношение можно было использовать в рамках другой операции (например, при объединении с другим отношением). | ||
'''Примеры''' | '''Примеры''' | ||
| + | |||
| + | Ниже приведен тривиальный пример-пояснение для операции переименования. | ||
| + | |||
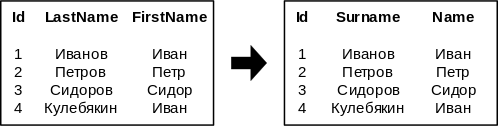
* <tex>\rho_{Name=FirstName, Surname=LastName}</tex> | * <tex>\rho_{Name=FirstName, Surname=LastName}</tex> | ||
[[Файл:Primitive_Rename_2.png]] | [[Файл:Primitive_Rename_2.png]] | ||
Версия 16:56, 22 декабря 2021
В этом разделе будут описаны унарные операции в рамках реляционной алгебры. В соответствии с определением, для определения каждой операции нужно указать способ построения заголовка, тела отношения, а также условия применимости, если такие есть.
Проекция
| Определение: |
| — проекция отношения на аттрибуты . Заголовок результирующего отношения: пересечение заголовка с . |
Данная операция полезна как минимум для следующего:
- Привести отношение к виду, в котором с ним можно будет осуществить другую операцию (например, объединение);
- Выбрать из отношения только нужные данные (для выборки).
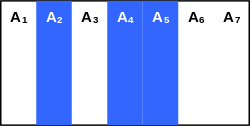
Ниже приведено пояснение определения для операции :
Синим обозначены столбцы, которые есть в результирующем отношении. Остальные столбцы не используются, и результат не зависит от данных, которые там находятся.
Примеры
Приведем несколько тривиальных примеров применения проекции.
Фильтрация
| Определение: |
| — фильтрация отношения по условию. Заголовок результирующего отношения равен заголовку исходного. |
Данная операция крайне часто используется для
- Ограничения области действия изменяющих запросов;
- Получения выборки данных, соответствующих определенному условию.
Примеры
Приведем несколько тривиальных примеров применения фильтрации.
- Можно писать и более сложные условия:
- Еще можно исопльзовать функции, доступные в БД:
Переименование
| Определение: |
| — изменение имени атрибута. Заголовок результирующего отношения равен заголовку исходного с точностью до изменения названий на . |
Операция часто применяется для того, чтобы отношение можно было использовать в рамках другой операции (например, при объединении с другим отношением).
Примеры
Ниже приведен тривиальный пример-пояснение для операции переименования.