Дерево отрезков. Построение — различия между версиями
| Строка 1: | Строка 1: | ||
| − | '''Дерево отрезков''' {{---}} это структура данных, которая позволяет эффективно (за асимптотику <tex>O(log n))</tex> реализовать операции следующего вида: нахождение суммы (задача RSQ), минимума или максимума (задача RMQ) элементов массива в заданном отрезке (<tex | + | '''Дерево отрезков''' {{---}} это структура данных, которая позволяет эффективно (за асимптотику <tex>O(log n))</tex> реализовать операции следующего вида: нахождение суммы (задача RSQ), минимума или максимума (задача RMQ) элементов массива в заданном отрезке (<tex>a[i...j]</tex>, где <tex>i</tex> и <tex>j</tex> поступают на вход алгоритма), при этом дополнительно возможно изменение элементов массива: как изменение значения одного элемента, так и изменение элементов на целом подотрезке массива (т.е. разрешается присвоить всем элементам <tex>a[i...j]</tex> какое-либо значение, либо прибавить ко всем элементам массива какое-либо число). Структура занимает <tex dpi = "140">O(n)</tex> памяти и выстраивается из массива за <tex>O(n)</tex>. |
==Структура== | ==Структура== | ||
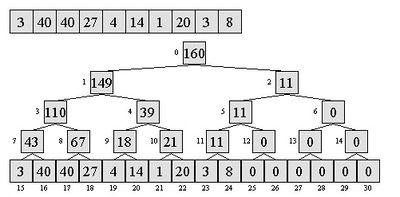
| − | [[Файл:Segment_tree.jpg|right|400px|thumb|Пример дерева отрезков для вычисления сумм]]Структура представляет собой дерево, листьями которого являются элементы исходного массива. Другие вершины этого дерева имеют по 2 ребёнка и содержат сумму или минимум/максимум своих детей (в зависимости от поставленной задачи). Таким образом, корень содержит результат искомой функции от всего массива <tex | + | [[Файл:Segment_tree.jpg|right|400px|thumb|Пример дерева отрезков для вычисления сумм]]Структура представляет собой дерево, листьями которого являются элементы исходного массива. Другие вершины этого дерева имеют по 2 ребёнка и содержат сумму или минимум/максимум своих детей (в зависимости от поставленной задачи). Таким образом, корень содержит результат искомой функции от всего массива <tex>[0...n-1]</tex>, левый ребёнок корня содержит результат функции на <tex>[0...n/2]</tex>, а правый, соответственно результат на <tex>[n/2+1...n-1]</tex>. И так далее, продвигаясь вглубь дерева. |
==Построение дерева== | ==Построение дерева== | ||
| − | Пусть исходный массив <tex | + | Пусть исходный массив <tex>a</tex> состоит из <tex>n</tex> элементов. Для удобства построения увеличим длину массива <tex dpi>a</tex> так, чтобы она равнялась ближайшей степени двойки, т.е. <tex>2^k</tex>, где <tex>2^k \ge n</tex>. Это сделано, для того чтобы не допустить обращение к несуществующим элементам массива при дальнейшем процессе построения. Пустые элементы можно заполнить нулями или бесконечностями (за бесконечностью стоит понимать, например, число, больше которого в данных ничего не появится) в зависимости от поставленной задачи. Тогда для хранения дерева отрезков понадобится массив <tex>t</tex> из <tex dpi = "140">2^{k+1}</tex> элементов, поскольку в худшем случае количество вершин в дереве можно оценить суммой <tex>n+n/2+n/4...+1 < 2n</tex>, где <tex>n=2^k</tex>. Таким образом, структура занимает линейную память. |
Далее будем считать, что дерево выстраиваем для задачи вычисления суммы на отрезке. Для минимума и максимума операция построения проделывается аналогично. | Далее будем считать, что дерево выстраиваем для задачи вычисления суммы на отрезке. Для минимума и максимума операция построения проделывается аналогично. | ||
| − | Процесс построения дерева заключается в заполнении массива <tex | + | Процесс построения дерева заключается в заполнении массива <tex>t</tex>. Заполним этот массив таким образом, чтобы <tex>i</tex>-й элемент являлся бы суммой элемента c номером <tex>2i</tex> и элемента с номером <tex>2i+1</tex>, т.е. родитель являлся бы суммой своих сыновей. Лучше всего эту процедуру делать рекурсивно. Создадим функцию от исходного массива <tex>a</tex>, переменной <tex>i</tex>, обозначающей номер элемента в массиве <tex>t</tex>, а так же переменные <tex>tl</tex> и <tex>tr</tex>, обозначающие соответственно левую и правую границы текущего отрезка. Запускаем процедуру построения от корня дерева отрезков (<tex>i=1</tex>, <tex>tl=0</tex>, <tex>tr=n-1</tex>), а сама процедура построения, если её вызвали не от листа, вызывает себя от каждого из двух сыновей и суммирует вычисленные значения, а если её вызвали от листа — то просто записывает в себя значение этого элемента массива. Асимптотика построения дерева отрезков составит, таким образом, <tex>O(n)</tex>. |
Реализация: | Реализация: | ||
Версия 22:07, 26 апреля 2011
Дерево отрезков — это структура данных, которая позволяет эффективно (за асимптотику реализовать операции следующего вида: нахождение суммы (задача RSQ), минимума или максимума (задача RMQ) элементов массива в заданном отрезке (, где и поступают на вход алгоритма), при этом дополнительно возможно изменение элементов массива: как изменение значения одного элемента, так и изменение элементов на целом подотрезке массива (т.е. разрешается присвоить всем элементам какое-либо значение, либо прибавить ко всем элементам массива какое-либо число). Структура занимает памяти и выстраивается из массива за .
Структура
Структура представляет собой дерево, листьями которого являются элементы исходного массива. Другие вершины этого дерева имеют по 2 ребёнка и содержат сумму или минимум/максимум своих детей (в зависимости от поставленной задачи). Таким образом, корень содержит результат искомой функции от всего массива , левый ребёнок корня содержит результат функции на , а правый, соответственно результат на . И так далее, продвигаясь вглубь дерева.Построение дерева
Пусть исходный массив состоит из элементов. Для удобства построения увеличим длину массива так, чтобы она равнялась ближайшей степени двойки, т.е. , где . Это сделано, для того чтобы не допустить обращение к несуществующим элементам массива при дальнейшем процессе построения. Пустые элементы можно заполнить нулями или бесконечностями (за бесконечностью стоит понимать, например, число, больше которого в данных ничего не появится) в зависимости от поставленной задачи. Тогда для хранения дерева отрезков понадобится массив из элементов, поскольку в худшем случае количество вершин в дереве можно оценить суммой , где . Таким образом, структура занимает линейную память.
Далее будем считать, что дерево выстраиваем для задачи вычисления суммы на отрезке. Для минимума и максимума операция построения проделывается аналогично.
Процесс построения дерева заключается в заполнении массива . Заполним этот массив таким образом, чтобы -й элемент являлся бы суммой элемента c номером и элемента с номером , т.е. родитель являлся бы суммой своих сыновей. Лучше всего эту процедуру делать рекурсивно. Создадим функцию от исходного массива , переменной , обозначающей номер элемента в массиве , а так же переменные и , обозначающие соответственно левую и правую границы текущего отрезка. Запускаем процедуру построения от корня дерева отрезков (, , ), а сама процедура построения, если её вызвали не от листа, вызывает себя от каждого из двух сыновей и суммирует вычисленные значения, а если её вызвали от листа — то просто записывает в себя значение этого элемента массива. Асимптотика построения дерева отрезков составит, таким образом, .
Реализация:
TreeBuild(a[], i, tl, tr)
if (tl = tr)
t[i] = a[tl];
else
tm = (tl + tr) / 2; //середина отрезка
TreeBuild(a, 2*v, tl, tm);
TreeBuild(a, 2*v+1, tm+1, tr);
t[v] = t[2*v] + t[2*v+1];
Ссылки
- Визуализатор дерева отрезков