Участник:Warmte — различия между версиями
Warmte (обсуждение | вклад) |
Warmte (обсуждение | вклад) |
||
| (не показаны 4 промежуточные версии этого же участника) | |||
| Строка 5: | Строка 5: | ||
==Точность== | ==Точность== | ||
| − | При использовании <tex>m</tex> единиц дополнительной памяти алгоритм '''HyperLogLog''' оценивает количество различных элементов со стандартной ошибкой около <tex>\frac{1.04}{\sqrt{m}}</tex>, | + | При использовании <tex>m</tex> единиц дополнительной памяти алгоритм '''HyperLogLog''' оценивает количество различных элементов со стандартной ошибкой около <tex>\frac{1.04}{\sqrt{m}}</tex>. Также этот алгоритм способен оценивать значения, превышающие 10<sup>9</sup>, используя 1.5 kB памяти для получения ответа с точностью 2%. |
Предыдущий алгоритм '''LogLog''', использовавшийся для решения этой задачи, достигал сравнимой точности ответа при использовании 64% от оригинальных объемов памяти. | Предыдущий алгоритм '''LogLog''', использовавшийся для решения этой задачи, достигал сравнимой точности ответа при использовании 64% от оригинальных объемов памяти. | ||
==Идея алгоритма== | ==Идея алгоритма== | ||
| − | + | {{Определение | |
| + | |definition= | ||
| + | Обозначим за '''мощность''' набора количество различных элементов в нём. | ||
| + | }} | ||
| − | + | В основе алгоритма '''HyperLogLog''' лежит наблюдение, что мощность набора [[wikipedia:ru:Равномерное_распределение|равномерно распределенных]] на заданном интервале <tex>[0, m-1]</tex> случайных чисел можно оценить, вычислив максимальное количество ведущих нулей в двоичном представлении каждого числа в наборе. Таким образом, если максимальное наблюдаемое количество начальных нулей равно <tex>n</tex>, то оценка количества различных элементов в наборе будет <tex>2^n</tex>. | |
| − | Но при таком подходе могут возникать различные проблемы за счёт большой дисперсии получаемой величины, а также некоторых крайних случаев: к примеру, если | + | Суть алгоритма заключается в следующем: к каждому элементу исходного набора применяется [[wikipedia:ru:Хеш-функция|хеш-функция]] для получения набора равномерно распределенных случайных чисел с той же мощностью, что и исходный набор. Затем мощность этого случайно распределенного набора оценивается с помощью описанного выше алгоритма. |
| + | |||
| + | Но при таком подходе могут возникать различные проблемы за счёт большой [[wikipedia:ru:Дисперсия_случайной_величины|дисперсии]] получаемой величины, а также некоторых крайних случаев: к примеру, если хеш некоторого элемента будет равен <tex>0</tex>, то максимальное количество ведущих нулей сразу станет равным <tex>\log_2{m}</tex>, где <tex>m</tex> {{---}} максимальное значение выбранной хеш-функции. Чтобы избежать подобных проблем и минимизировать дисперсию, модифицируем алгоритм следующим образом: разделим исходный поток элементов на <tex>2^r</tex> корзин, для каждой из них вычислим максимальное наблюдаемое количество начальных нулей среди элементов в этой корзине, а затем на основе полученных для всех корзин значений вычислим итоговый ответ на задачу. | ||
==Описание алгоритма== | ==Описание алгоритма== | ||
| − | *<tex>\mathcal{M}</tex> {{---}} исходный набор элементов <tex>a_1 ... a_n</tex>. | + | * <tex>\mathcal{M}</tex> {{---}} исходный набор элементов <tex>a_1 ... a_n</tex>. |
| − | *<tex>h : \mathcal{U} \to {0, 1 ... 2^k - 1}</tex> {{---}} выбранная | + | * <tex>h : \mathcal{U} \to {0, 1 ... 2^k-1}</tex> {{---}} выбранная хеш-функция с возможными значениями от <tex>0</tex> до <tex>m-1</tex>, <tex>k = \log_2{m}</tex>. |
| − | *<tex>r</tex> {{---}} количество бит исходного | + | * <tex>r</tex> {{---}} количество бит исходного хеша, характеризующих номер корзины, в которую будет отправлен соответствующий элемент. |
| − | *<tex>z_j</tex> {{---}} максимальное наблюдаемое количество начальных нулей в корзине под номером <tex>j</tex>. | + | * <tex>z_j</tex> {{---}} максимальное наблюдаемое количество начальных нулей в корзине под номером <tex>j</tex>. |
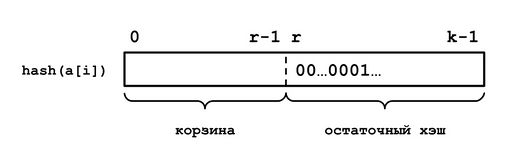
| − | Разобьём исходный набор <tex>\mathcal{M}</tex> на наборы <tex>\mathcal{M}_0..\mathcal{M}_{2^r - 1}</tex> следующим образом: для каждого поступающего элемента <tex>a_i</tex> вычислим его | + | Разобьём исходный набор <tex>\mathcal{M}</tex> на наборы <tex>\mathcal{M}_0..\mathcal{M}_{2^r - 1}</tex> следующим образом: для каждого поступающего элемента <tex>a_i</tex> вычислим его хеш <tex>h(a_i)</tex> и представим его в двоичном виде. Тогда первые <tex>r</tex> бит этого двоичного представления будут характеризовать номер корзины <tex>j</tex>, а оставшиеся биты сформируют остаточный хеш <tex>h'(a_i)</tex>, который и будет использоваться для поиска максимального количества начальных нулей в корзине <tex>\mathcal{M}_j</tex>. |
[[Файл:Hll_bins.jpg|512px]] | [[Файл:Hll_bins.jpg|512px]] | ||
| Строка 31: | Строка 36: | ||
Для каждой корзины вычислим соответствующее <tex>z_j</tex>, равное максимальному количеству ведущих нулей среди элементов этой корзины. Тогда оценкой для числа различных элементов в корзине будет <tex>2^{z_j}</tex>. | Для каждой корзины вычислим соответствующее <tex>z_j</tex>, равное максимальному количеству ведущих нулей среди элементов этой корзины. Тогда оценкой для числа различных элементов в корзине будет <tex>2^{z_j}</tex>. | ||
| − | Логично было бы предположить, что в таком случае итоговым ответом на задачу будет <tex> \sum\limits_{j=0}^{2^{r - 1}} 2^{z_j} </tex>, но такой подход приводит не к самому выгодному результату. Выгоднее всего будет пересчитывать результат при помощи среднего гармонического всех полученных оценок: | + | Логично было бы предположить, что в таком случае итоговым ответом на задачу будет <tex> \sum\limits_{j=0}^{2^{r - 1}} 2^{z_j} </tex>, но такой подход приводит не к самому выгодному результату. Выгоднее всего будет пересчитывать результат при помощи среднего гармонического всех полученных оценок: <tex>E \approx \alpha \cdot (2^r)^2 \cdot I</tex> |
| + | |||
| + | <tex>I</tex> {{---}} это индикатор, вычисляемый по формуле <tex>I = (\sum\limits_{j=0}^{2^{r - 1}} \frac{1}{2^{z_j}})^{-1} </tex> | ||
| + | |||
| + | <tex>\alpha</tex> {{---}} корректирующий множитель, вычисляемый по формуле <tex>\alpha = (2^r \int\limits_{0}^{\infty} (\log_2{\frac{2 + u}{1 + u}})^{2^r} \,du )^{-1}</tex>. | ||
| + | |||
| + | Поскольку множитель <tex>\alpha</tex> может быть достаточно сложным для вычисления, можно подобрать его примерное значение в зависимости от <tex>r</tex>: | ||
| − | <tex> | + | <tex> |
| + | \alpha_{r}\approx\begin{cases} | ||
| + | r=4 & 0.673\\ | ||
| + | r=5 & 0.697\\ | ||
| + | r=6 & 0.709\\ | ||
| + | r\ge7 & \frac{0.7213}{1+\frac{1.079}{2^r}} | ||
| + | \end{cases} | ||
| + | </tex> | ||
| − | + | Число <tex>E</tex> и будет итоговой оценкой мощности данного набора. | |
| − | + | ==План доказательства== | |
| + | {{Определение | ||
| + | |definition= | ||
| + | '''Идеальным мультимножеством''' мощностью <tex>n</tex> называется последовательность, полученная произвольными повторениями и перестановками, применяемыми к <tex>n</tex> равномерно распределенным случайным величинам на действительном интервале [0, 1]. | ||
| + | }} | ||
| − | + | {{Теорема | |
| + | |statement= | ||
| + | Пусть алгоритм '''HyperLogLog''' применяется к идеальному мультимножеству мощностью <tex>n</tex> (число <tex>n</tex> нам неизвестно), используя <tex>reg = 2^r</tex> корзин, и пусть <tex>E</tex> {{---}} полученная результирующая оценка количества различных элементов в этом мультимножестве. | ||
| + | |||
| + | # Оценка величины E в таком случае асимптотически почти несмещенная, а именно: <br /> <tex> \frac{1}{n} \mathbb{E}(E) \overset{n \to \infty}{=} 1 + \delta_1(n) + o(1)</tex>, где <tex>|\delta_1(n)| < 5 \cdot 10^{-5}</tex> при <tex>reg \geq 16</tex> | ||
| + | # Стандартная ошибка, равная <tex>\frac{1}{n}\sqrt{\mathbb{D}_n(E)}</tex>, вычисляется следующим образом: <br /> <tex>\frac{1}{n}\sqrt{\mathbb{D}_n(E)} \overset{n \to \infty}{=} \frac{\beta_{reg}}{\sqrt{reg}} + \delta_2(n) + o(1)</tex>, где <tex>|\delta_2(n)| < 5 \cdot 10^{-4}</tex> при <tex>reg \geq 16</tex> | ||
| + | <tex>\delta_1(n)</tex>, <tex>\delta_2(n)</tex> представляют собой осциллирующие функции с маленькой амплитудой, поддающиеся вычислению. Хотя их влияние в теории может быть компенсировано только частично, ими можно безопасно пренебречь для всех практических целей. | ||
| + | Константа <tex>\beta_{reg}</tex>, в свою очередь, вычисляется следующим образом: | ||
:<tex> | :<tex> | ||
| − | \ | + | \beta_{reg}=\begin{cases} |
| − | + | reg=16 & 1.106\\ | |
| − | + | reg=32 & 1.070\\ | |
| − | + | reg=64 & 1.054\\ | |
| − | + | reg=126 & 1.046\\ | |
| + | reg\to\infty & \sqrt{3 \log(2) - 1} = 1.03896 | ||
\end{cases} | \end{cases} | ||
</tex> | </tex> | ||
| + | }} | ||
| + | |||
| + | Основная задача представляет оценку асимптотической зависимости величин <tex>\mathbb{E}_n</tex> и <tex>\mathbb{D}_n</tex> от индикатора <tex>Z = \frac{1}{\sum 2^{-z_j}}</tex>. | ||
| + | |||
| + | Краткий план доказательства имеет следующий вид: | ||
| + | |||
| + | # Сначала выводятся значение величины <tex>\alpha_r</tex>, которая и делает оценку <tex>E</tex> асимптотически почти несмещенной, и величина стандартной ошибки. | ||
| + | # Затем производится непосредственная оценка величин <tex>\mathbb{E}_n(Z)</tex> и <tex>\mathbb{D}_n(Z)</tex>. | ||
| + | # Поскольку значение <tex>\mathbb{E}_n(Z)</tex> достаточно сложно вычислить, сначала исследуется величина <tex>\mathbb{E}_{\mathcal{P}(\lambda)}(Z)</tex>, то есть ситуация, когда ожидаемое значение величины <tex>Z</tex> не фиксировано, а удовлетворяет закону Пуассона с некоторым параметром <tex>\lambda</tex>. | ||
| + | # После этого остаётся доказать, что при <tex>\lambda := n</tex> поведение <tex>\mathbb{E}_n(Z)</tex> и <tex>\mathbb{E}_{\mathcal{P}(\lambda)}(Z)</tex> асимптотически близко. | ||
| + | |||
| + | С полным доказательством этой теоремы можно ознакомиться в [http://algo.inria.fr/flajolet/Publications/FlFuGaMe07.pdf оригинальной статье]. | ||
==Асимптотика== | ==Асимптотика== | ||
Оценка времени работы: <tex>\mathcal{O}(n)</tex>, где <tex>n</tex> {{---}} количество элементов в исходном наборе. | Оценка времени работы: <tex>\mathcal{O}(n)</tex>, где <tex>n</tex> {{---}} количество элементов в исходном наборе. | ||
| − | Оценка дополнительной памяти: <tex> | + | Оценка дополнительной памяти: <tex>\mathcal{O}(2^r \cdot \log_2 \log_2 n) </tex>. |
| + | ==Практические оптимизации== | ||
| + | Полученное при помощи алгоритма '''HyperLogLog''' значение <tex>E</tex> может оказаться неточным и нуждается в корректировке: | ||
| + | * При <tex>E \leq \frac{5}{2}2^r</tex> в оценке могут появляться нелинейные искажения, которые необходимо скорректировать. Вычислим количество <tex>z_j</tex> равных <tex>0</tex>, обозначим эту величину за <tex>V</tex>. Если <tex>V = 0</tex>, то уже полученное алгоритмом значение <tex>E</tex> в корректировке не нуждается, иначе оно должно быть вычислено по формуле <tex>E_{result} = 2^r \log(\frac{2^r}{V})</tex>. | ||
| + | * В том случае, если значение <tex>E</tex> превосходит ограничение на размер <tex>z_j</tex>, возрастает вероятность коллизии при хешировании и итоговая оценка также должна быть скорректирована. Рассмотрим 32-битный случай: при <tex>E > \frac{2^{32}}{30}</tex> итоговое значение можно вычислить как <tex>E_{result} = -2^{32} \log(1 - \frac{E}{2^{32}})</tex>. | ||
| + | * В остальных случаях итоговая оценка <tex>E</tex> в корректировке не нуждается. | ||
| − | == | + | ==Литература== |
*[[wikipedia:en:HyperLogLog | Wikipedia {{---}} HyperLogLog algorithm]] | *[[wikipedia:en:HyperLogLog | Wikipedia {{---}} HyperLogLog algorithm]] | ||
*[http://algo.inria.fr/flajolet/Publications/FlFuGaMe07.pdf Philippe Flajolet, Éric Fusy, Olivier Gandouet and Frédéric Meunier {{---}} HyperLogLog: the analysis of a near-optimal cardinality estimation algorithm] | *[http://algo.inria.fr/flajolet/Publications/FlFuGaMe07.pdf Philippe Flajolet, Éric Fusy, Olivier Gandouet and Frédéric Meunier {{---}} HyperLogLog: the analysis of a near-optimal cardinality estimation algorithm] | ||
[[Категория: Продвинутые алгоритмы]] | [[Категория: Продвинутые алгоритмы]] | ||
| − | |||
[[Категория: Вероятностные алгоритмы]] | [[Категория: Вероятностные алгоритмы]] | ||
Текущая версия на 22:05, 24 января 2022
HyperLogLog — это вероятностный алгоритм, оценивающий количество различных элементов в больших потоках данных. Является стриминговым алгоритмом (англ. streaming algorithm), то есть обрабатывает последовательно поступающие данные в один проход.
Подобные алгоритмы используются в тех случаях, когда объемы обрабатываемых данных настолько велики, что получение точного ответа затребует пропорционально слишком большого объёма памяти, в то время как вероятностный алгоритм может дать близкий к точному ответ, будучи с точки зрения памяти намного более оптимальным.
Содержание
Точность
При использовании единиц дополнительной памяти алгоритм HyperLogLog оценивает количество различных элементов со стандартной ошибкой около . Также этот алгоритм способен оценивать значения, превышающие 109, используя 1.5 kB памяти для получения ответа с точностью 2%.
Предыдущий алгоритм LogLog, использовавшийся для решения этой задачи, достигал сравнимой точности ответа при использовании 64% от оригинальных объемов памяти.
Идея алгоритма
| Определение: |
| Обозначим за мощность набора количество различных элементов в нём. |
В основе алгоритма HyperLogLog лежит наблюдение, что мощность набора равномерно распределенных на заданном интервале случайных чисел можно оценить, вычислив максимальное количество ведущих нулей в двоичном представлении каждого числа в наборе. Таким образом, если максимальное наблюдаемое количество начальных нулей равно , то оценка количества различных элементов в наборе будет .
Суть алгоритма заключается в следующем: к каждому элементу исходного набора применяется хеш-функция для получения набора равномерно распределенных случайных чисел с той же мощностью, что и исходный набор. Затем мощность этого случайно распределенного набора оценивается с помощью описанного выше алгоритма.
Но при таком подходе могут возникать различные проблемы за счёт большой дисперсии получаемой величины, а также некоторых крайних случаев: к примеру, если хеш некоторого элемента будет равен , то максимальное количество ведущих нулей сразу станет равным , где — максимальное значение выбранной хеш-функции. Чтобы избежать подобных проблем и минимизировать дисперсию, модифицируем алгоритм следующим образом: разделим исходный поток элементов на корзин, для каждой из них вычислим максимальное наблюдаемое количество начальных нулей среди элементов в этой корзине, а затем на основе полученных для всех корзин значений вычислим итоговый ответ на задачу.
Описание алгоритма
- — исходный набор элементов .
- — выбранная хеш-функция с возможными значениями от до , .
- — количество бит исходного хеша, характеризующих номер корзины, в которую будет отправлен соответствующий элемент.
- — максимальное наблюдаемое количество начальных нулей в корзине под номером .
Разобьём исходный набор на наборы следующим образом: для каждого поступающего элемента вычислим его хеш и представим его в двоичном виде. Тогда первые бит этого двоичного представления будут характеризовать номер корзины , а оставшиеся биты сформируют остаточный хеш , который и будет использоваться для поиска максимального количества начальных нулей в корзине .
Для каждой корзины вычислим соответствующее , равное максимальному количеству ведущих нулей среди элементов этой корзины. Тогда оценкой для числа различных элементов в корзине будет .
Логично было бы предположить, что в таком случае итоговым ответом на задачу будет , но такой подход приводит не к самому выгодному результату. Выгоднее всего будет пересчитывать результат при помощи среднего гармонического всех полученных оценок:
— это индикатор, вычисляемый по формуле
— корректирующий множитель, вычисляемый по формуле .
Поскольку множитель может быть достаточно сложным для вычисления, можно подобрать его примерное значение в зависимости от :
Число и будет итоговой оценкой мощности данного набора.
План доказательства
| Определение: |
| Идеальным мультимножеством мощностью называется последовательность, полученная произвольными повторениями и перестановками, применяемыми к равномерно распределенным случайным величинам на действительном интервале [0, 1]. |
| Теорема: |
Пусть алгоритм HyperLogLog применяется к идеальному мультимножеству мощностью (число нам неизвестно), используя корзин, и пусть — полученная результирующая оценка количества различных элементов в этом мультимножестве.
, представляют собой осциллирующие функции с маленькой амплитудой, поддающиеся вычислению. Хотя их влияние в теории может быть компенсировано только частично, ими можно безопасно пренебречь для всех практических целей. Константа , в свою очередь, вычисляется следующим образом: |
Основная задача представляет оценку асимптотической зависимости величин и от индикатора .
Краткий план доказательства имеет следующий вид:
- Сначала выводятся значение величины , которая и делает оценку асимптотически почти несмещенной, и величина стандартной ошибки.
- Затем производится непосредственная оценка величин и .
- Поскольку значение достаточно сложно вычислить, сначала исследуется величина , то есть ситуация, когда ожидаемое значение величины не фиксировано, а удовлетворяет закону Пуассона с некоторым параметром .
- После этого остаётся доказать, что при поведение и асимптотически близко.
С полным доказательством этой теоремы можно ознакомиться в оригинальной статье.
Асимптотика
Оценка времени работы: , где — количество элементов в исходном наборе.
Оценка дополнительной памяти: .
Практические оптимизации
Полученное при помощи алгоритма HyperLogLog значение может оказаться неточным и нуждается в корректировке:
- При в оценке могут появляться нелинейные искажения, которые необходимо скорректировать. Вычислим количество равных , обозначим эту величину за . Если , то уже полученное алгоритмом значение в корректировке не нуждается, иначе оно должно быть вычислено по формуле .
- В том случае, если значение превосходит ограничение на размер , возрастает вероятность коллизии при хешировании и итоговая оценка также должна быть скорректирована. Рассмотрим 32-битный случай: при итоговое значение можно вычислить как .
- В остальных случаях итоговая оценка в корректировке не нуждается.