Формула Эйлера

НЕТ ВОЙНЕ

24 февраля 2022 года российское руководство во главе с Владимиром Путиным развязало агрессивную войну против Украины. В глазах всего мира это военное преступление совершено от лица всей страны, всех россиян. Будучи гражданами Российской Федерации, мы против своей воли оказались ответственными за нарушение международного права, военное вторжение и массовую гибель людей. Чудовищность совершенного преступления не оставляет возможности промолчать или ограничиться пассивным несогласием. Мы убеждены в абсолютной ценности человеческой жизни, в незыблемости прав и свобод личности. Режим Путина — угроза этим ценностям. Наша задача — обьединить все силы для сопротивления ей. Эту войну начали не россияне, а обезумевший диктатор. И наш гражданский долг — сделать всё, чтобы её остановить. Антивоенный комитет России

Распространяйте правду о текущих событиях, оберегайте от пропаганды своих друзей и близких. Изменение общественного восприятия войны - ключ к её завершению.

meduza.io, Популярная политика, Новая газета, zona.media, Майкл Наки.

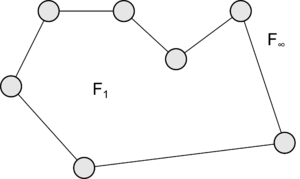
Двумерный случай

Теорема (формула Эйлера):

Для произвольного плоского связного графа [math]G[/math] с [math]V[/math] вершинами, [math]E[/math] ребрами и [math]F[/math] гранями справедливо следующее соотношение: [math]V - E + F = 2[/math]

Доказательство:

[math]\triangleright[/math]

Воспользуемся методом математической индукции по количеству граней графа. База индукции: [math]F = 2[/math]. Граф [math]G[/math] представляет собой многоугольник с [math]n[/math] вершинами (рис. 1). Тогда [math]V = E = n[/math], значит, равенство [math]V - E + F = 2[/math] выполняется. Индукционный переход: Покажем, что если теорема верна для графов с [math]F[/math] гранями, то она будет верна и для графов с [math]F + 1[/math] гранями. Пусть [math]G[/math] — плоский граф, имеющий [math]V[/math] вершин, [math]E[/math] ребер и [math]F[/math] граней, и для него справедлива формула Эйлера. Добавим новую грань (пунктирная линия на рис.2), проводя по внешней грани [math]F_{\infty}[/math] некоторую элементарную цепь, соединяющую две вершины максимального цикла графа [math]G[/math]. Если эта цепь имеет [math]r[/math] ребер, то необходимо добавить [math]r - 1[/math] новых вершин и одну новую грань. Ясно, что формула Эйлера останется справедливой и для нового графа, так как [math]V' - E' + F' = (V + r - 1) - (E + r) + (F + 1) = V - E + F = 2[/math]

[math]\triangleleft[/math]

рис. 1

рис. 2

Теорема (следствие из формулы Эйлера):

Пусть [math]G[/math] связный планарный обыкновенный граф с [math]V[/math] вершинами ([math]V \geqslant 3[/math]), [math]E[/math] ребрами и [math]F[/math] гранями. Тогда [math]E \leqslant 3V - 6[/math]

Доказательство:

[math]\triangleright[/math]

Поскольку [math]G[/math] не содержит петель и кратных ребер, то каждая грань граничит хотя бы с тремя ребрами. Пусть, двигаясь вдоль [math]i[/math]-й грани мы пройдем [math]l_i[/math] ребер. Очевидно, что [math]\sum \limits_{i=1}^{F}l_i = 2E[/math]. Поскольку [math]l_i \geqslant 3 \hspace{3pt} (i = 1..F)[/math], получаем [math]3F \leqslant 2E[/math]. Из формулы Эйлера [math]3E - 3V + 6 = 3F \leqslant 2E[/math], то есть [math]E \leqslant 3V - 6[/math].

[math]\triangleleft[/math]

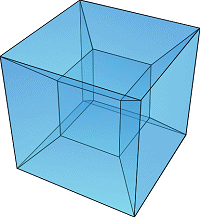
Трехмерный случай

Покажем, что в трехмерном случае так же имеет место формула Эйлера.

Теорема (формула Эйлера для многогранников):

Для любого выпуклого многогранника имеет место равенство [math]V - E + F = 2[/math], где [math]V[/math] — число вершин, [math]E[/math] — число ребер и [math]F[/math] — число граней данного многогранника.

Доказательство:

[math]\triangleright[/math]

Пример невыпуклого многоугольника для которого [math]V - E + F = 0[/math]. Многоугольник получен путем вырезания куба внутри куба. Для доказательства соотношения Эйлера представим поверхность выпуклого многогранника сделанной из эластичного материала. Удалим (вырежем) одну из его граней и оставшуюся поверхность растянем на плоскости. Получим планарный граф, содержащий [math]F' = F - 1[/math] внутренних граней, [math]V[/math] вершин и [math]E[/math] ребер. Тогда справедливо уже доказанное соотношение: [math]V - E + F ' = 1 [/math]. Подставляем [math]F' = F - 1[/math] и получаем [math]V - E + F = 2[/math].

[math]\triangleleft[/math]

Теорема (следствие из формулы Эйлера для многогранников):

В любом выпуклом многограннике имеется или треугольная грань, или трехгранный угол. Более того, число треугольных граней плюс число трехгранных углов больше или равно восьми.

Доказательство:

[math]\triangleright[/math]

Обозначим через [math]V_{i}[/math] число вершин выпуклого многогранника, в которых сходится [math]i[/math] ребер. Тогда для общего числа вершин [math]V[/math] имеет место равенство [math]V = V_{3} + V_{4} + V_{5} + \dots[/math] Аналогично, обозначим через [math]F_{i}[/math] число граней выпуклого многогранника, у которых имеется [math]i[/math] ребер. Тогда для общего числа граней [math]F[/math] имеет место равенство [math]F = F_{3} + F_{4} + F_{5} + \dots[/math] Посчитаем число ребер [math]E[/math] многогранника. Имеем: [math]3V_{3} + 4V_{4} + 5V_{5} + \dots = 2E[/math], [math]3F_{3} + 4F_{4} + 5F_{5} + \dots = 2E[/math]. По теореме Эйлера выполняется равенство [math]4V - 4E + 4F = 8[/math]. Подставляя вместо [math]V[/math], [math]E[/math] и [math]F[/math] их выражения, получим: [math]4V_{3} + 4V_{4} + 4V_{5} + \dots - (3V_{3} + 4V_{4} + 5V_{5} + \dots) - (3F_{3} + 4F_{4} + 5F_{5} + \dots) + 4F_{3} + 4F_{4} + 4F_{5} + \dots = 8[/math]. Следовательно, [math]V_{3} + F_{3} = 8 + V_{5} + \dots + F_{5} + \dots [/math], значит, число треугольных граней плюс число трехгранных углов больше или равно восьми.

[math]\triangleleft[/math]

Источники информации

• Асанов М,, Баранский В., Расин В. — Дискретная математика — Графы, матроиды, алгоритмы (стр. 104-107)
• О.Оре — Графы и их применение (стр. 131-135)
• Википедия — Теорема Эйлера для многоугольников
• Выпуклые многогранники