Производные некоторых элементарных функций — различия между версиями
Rybak (обсуждение | вклад) м (→Первый замечательный предел: \frac12) |
|||
| Строка 1: | Строка 1: | ||
| + | {| class="wikitable" align="center" style="color: red; background-color: black; font-size: 56px; width: 800px;" | ||
| + | |+ | ||
| + | |-align="center" | ||
| + | |'''НЕТ ВОЙНЕ''' | ||
| + | |-style="font-size: 16px;" | ||
| + | | | ||
| + | 24 февраля 2022 года российское руководство во главе с Владимиром Путиным развязало агрессивную войну против Украины. В глазах всего мира это военное преступление совершено от лица всей страны, всех россиян. | ||
| + | |||
| + | Будучи гражданами Российской Федерации, мы против своей воли оказались ответственными за нарушение международного права, военное вторжение и массовую гибель людей. Чудовищность совершенного преступления не оставляет возможности промолчать или ограничиться пассивным несогласием. | ||
| + | |||
| + | Мы убеждены в абсолютной ценности человеческой жизни, в незыблемости прав и свобод личности. Режим Путина — угроза этим ценностям. Наша задача — обьединить все силы для сопротивления ей. | ||
| + | |||
| + | Эту войну начали не россияне, а обезумевший диктатор. И наш гражданский долг — сделать всё, чтобы её остановить. | ||
| + | |||
| + | ''Антивоенный комитет России'' | ||
| + | |-style="font-size: 16px;" | ||
| + | |Распространяйте правду о текущих событиях, оберегайте от пропаганды своих друзей и близких. Изменение общественного восприятия войны - ключ к её завершению. | ||
| + | |-style="font-size: 16px;" | ||
| + | |[https://meduza.io/ meduza.io], [https://www.youtube.com/c/popularpolitics/videos Популярная политика], [https://novayagazeta.ru/ Новая газета], [https://zona.media/ zona.media], [https://www.youtube.com/c/MackNack/videos Майкл Наки]. | ||
| + | |} | ||
| + | |||
== Вычисление некоторых пределов == | == Вычисление некоторых пределов == | ||
Версия 07:52, 1 сентября 2022
| НЕТ ВОЙНЕ |
|
24 февраля 2022 года российское руководство во главе с Владимиром Путиным развязало агрессивную войну против Украины. В глазах всего мира это военное преступление совершено от лица всей страны, всех россиян. Будучи гражданами Российской Федерации, мы против своей воли оказались ответственными за нарушение международного права, военное вторжение и массовую гибель людей. Чудовищность совершенного преступления не оставляет возможности промолчать или ограничиться пассивным несогласием. Мы убеждены в абсолютной ценности человеческой жизни, в незыблемости прав и свобод личности. Режим Путина — угроза этим ценностям. Наша задача — обьединить все силы для сопротивления ей. Эту войну начали не россияне, а обезумевший диктатор. И наш гражданский долг — сделать всё, чтобы её остановить. Антивоенный комитет России |
| Распространяйте правду о текущих событиях, оберегайте от пропаганды своих друзей и близких. Изменение общественного восприятия войны - ключ к её завершению. |
| meduza.io, Популярная политика, Новая газета, zona.media, Майкл Наки. |
Содержание
Вычисление некоторых пределов
Вычислим предварительно ряд важных пределов.
Первый замечательный предел
| Утверждение: |
|
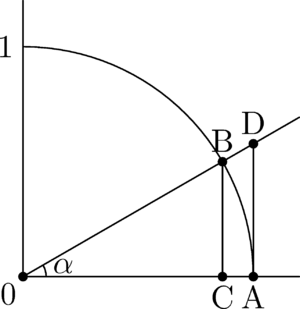
В теории степенных рядов синус определён как сумма ряда. Сейчас для доказательства, однако, воспользуемся геометрическим смыслом синуса. Рассмотрим радианную меру угла , равную отношению длины дуги к радиусу окружности. В частности, при , длина дуги совпадает с величиной угла.
Сектор
. Запомним этот факт. Площадь сектора равна , а . Тогда Но тогда, . Но так как Тогда . |
Второй замечательный предел
| Определение: |
Из этого, подставив , получим
Далее, прологарифмировав последнее равенство, получим: при стремится к .
(e^x - 1)/x
| Утверждение: |
при |
|
(подставив ) . Тогда |
Рассмотрим выражение . Оно (?)создаёт неопределённость . При этом, предел нельзя
вычислить переходом к нему в числителе и знаменателе по отдельности. Этот предел подстановкой сводится к предыдущим.
Вычисление производных некоторых функций
y = x^n
n — целое
| Утверждение: |
|
Докажем по индукции.
Это соответствует функции . Тогда Тогда
|
Заметим, что если непрерывна и монотонна в окрестности , а также, , то обратная функция дифференцируема в , и её производная равна . Это следует из того факта, что .
1/n; n — целое
| Утверждение: |
Посчитаем |
|
Согласно формуле дифференцирования обратной функции, . |
Подведём промежуточный итог. Мы научились считать
n — рациональное
| Утверждение: |
. |
| (подставив ) |
Важное Замечание: — не степенная функция. Все реальные пацаны считают это по определению равным
e^x
| Утверждение: |
|
Тогда . Ранее мы доказали, что . Тогда . Это единственная функция, которая обладает таким свойством(это просто забавный факт, его не надо доказывать). Именно поэтому занимает такое важное место в математике. |
ln(x)
| Утверждение: |
|
. Тогда . |
sin(x)
| Утверждение: |
|
Пусть .
Первый множитель, равный вычисленному ранее пределу, равен , а второй при стремится к . Тогда . |
arcsin(x)
| Утверждение: |
|
. Тогда . Так как , то Получаем . |