Связь максимального паросочетания и минимального вершинного покрытия в двудольных графах

НЕТ ВОЙНЕ

24 февраля 2022 года российское руководство во главе с Владимиром Путиным развязало агрессивную войну против Украины. В глазах всего мира это военное преступление совершено от лица всей страны, всех россиян. Будучи гражданами Российской Федерации, мы против своей воли оказались ответственными за нарушение международного права, военное вторжение и массовую гибель людей. Чудовищность совершенного преступления не оставляет возможности промолчать или ограничиться пассивным несогласием. Мы убеждены в абсолютной ценности человеческой жизни, в незыблемости прав и свобод личности. Режим Путина — угроза этим ценностям. Наша задача — обьединить все силы для сопротивления ей. Эту войну начали не россияне, а обезумевший диктатор. И наш гражданский долг — сделать всё, чтобы её остановить. Антивоенный комитет России

Распространяйте правду о текущих событиях, оберегайте от пропаганды своих друзей и близких. Изменение общественного восприятия войны - ключ к её завершению.

meduza.io, Популярная политика, Новая газета, zona.media, Майкл Наки.

Минимальное вершинное покрытие

Определение:

Вершинным покрытием (англ. vertex covering) графа [math]G=(V,E)[/math] называется такое подмножество [math]S[/math] множества вершин графа [math]V[/math], что любое ребро этого графа инцидентно хотя бы одной вершине из множества [math]S[/math].

Определение:

Минимальным вершинным покрытием (англ. minimum vertex covering) графа [math]G=(V,E)[/math] называется вершинное покрытие, состоящее из наименьшего числа вершин.

Множество вершин красного цвета — минимальное вершинное покрытие.

Теорема о мощности минимального вершинного покрытия и максимального паросочетания

Определение:

Максимальным паросочетанием (англ. maximum matching) в двудольном графе [math]G[/math] называется паросочетание максимальной мощности.

Теорема (Кёниг):

В произвольном двудольном графе мощность максимального паросочетания равна мощности минимального вершинного покрытия.

Доказательство:

[math]\triangleright[/math]

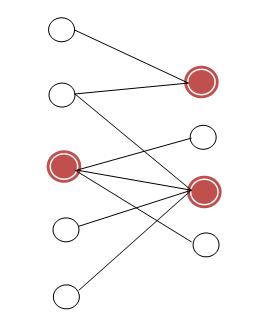
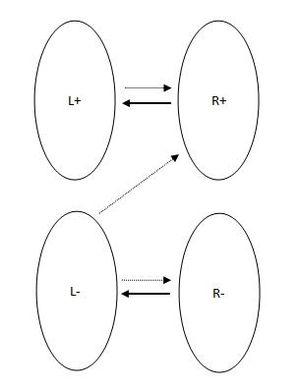
Пусть в [math]G[/math] построено максимальное паросочетание. Ориентируем ребра паросочетания, чтобы они шли из правой доли в левую, ребра не из паросочетания — так, чтобы они шли из левой доли в правую. Запустим обход в глубину из всех не насыщенных паросочетанием вершин левой доли. Разобьем вершины каждой доли графа на два множества: те, которые были посещены в процессе обхода, и те, которые не были посещены в процессе обхода. Тогда [math]L = L^+ \cup L^-[/math], [math]R = R^+ \cup R^-[/math], где [math]L, R[/math] — правая и левая доли соответственно, [math]L^+, R^+[/math] — вершины правой и левой доли, посещенные обходом, [math]L^-, R^-[/math] — не посещенные обходом вершины. Тогда в [math]G[/math] могут быть следующие ребра: Доли [math]L^+, L^-, R^+, R^-[/math] и ребра между ними. Из вершин [math]L^+[/math] в вершины [math]R^+[/math] и из вершин [math]R^+[/math] в вершины [math]L^+[/math]. Из вершин [math]L^-[/math] в вершины [math]R^-[/math] и из вершин [math]R^-[/math] в вершины [math]L^-[/math]. Из вершин [math]L^-[/math] в вершины [math]R^+[/math]. Очевидно, что ребер из [math]L^+[/math] в [math]R^-[/math] и из [math]R^+[/math] в [math]L^-[/math] быть не может. Ребер из [math]R^-[/math] в [math]L^+[/math] быть не может, т.к. если такое ребро [math]uv[/math] существует, то оно — ребро паросочетания. Тогда вершина [math]v[/math] насыщена паросочетанием. Но т.к. [math]v \in L^+[/math], то в нее можно дойти из какой-то ненасыщенной вершины левой доли. Значит, существует ребро [math]wv, w \in R^+[/math]. Но тогда [math]v[/math] инцидентны два ребра из паросочетания. Противоречие. Заметим, что минимальным вершинным покрытием [math]G[/math] является либо [math]L[/math], либо [math]R[/math], либо [math]L^- \cup R^+[/math]. В [math]R^+[/math] не насыщенных паросочетанием вершин быть не может, т.к. иначе в [math]G[/math] существует дополняющая цепь, что противоречит максимальности построенного паросочетания. В [math]L^-[/math] свободных вершин быть не может, т.к. все они должны находиться в [math]L^+[/math]. Тогда т.к. ребер из паросочетания между [math]R^+[/math] и [math]L^-[/math] нет, то каждому ребру максимального паросочетания инцидентна ровно одна вершина из [math]L^- \cup R^+[/math]. Тогда [math]|L^- \cup R^+|[/math] равна мощности максимального паросочетания. Множество вершин [math]L^- \cup R^+[/math] является минимальным вершинным покрытием. Значит мощность максимального паросочетания равна мощности минимального вершинного покрытия.

[math]\triangleleft[/math]

Алгоритм построения минимального вершинного покрытия

Из доказательства предыдущей теоремы следует алгоритм поиска минимального вершинного покрытия графа:

1. Построить максимальное паросочетание.
2. Ориентировать ребра:
   • Из паросочетания — из правой доли в левую.
   • Не из паросочетания — из левой доли в правую.
3. Запустить обход в глубину из всех свободных вершин левой доли, построить множества [math]L^+,L^-,R^+,R^-[/math].
4. В качестве результата взять [math]L^- \cup R^+[/math].

См. также

• Теорема о максимальном паросочетании и дополняющих цепях
• Связь вершинного покрытия и независимого множества

Источники информации

• Википедия — Теорема Кёнига