Связь между максимизацией гиперобъема и аппроксимацией Парето-фронта — различия между версиями
м |
|||
| Строка 1: | Строка 1: | ||
| + | {| class="wikitable" align="center" style="color: red; background-color: black; font-size: 56px; width: 800px;" | ||
| + | |+ | ||
| + | |-align="center" | ||
| + | |'''НЕТ ВОЙНЕ''' | ||
| + | |-style="font-size: 16px;" | ||
| + | | | ||
| + | 24 февраля 2022 года российское руководство во главе с Владимиром Путиным развязало агрессивную войну против Украины. В глазах всего мира это военное преступление совершено от лица всей страны, всех россиян. | ||
| + | |||
| + | Будучи гражданами Российской Федерации, мы против своей воли оказались ответственными за нарушение международного права, военное вторжение и массовую гибель людей. Чудовищность совершенного преступления не оставляет возможности промолчать или ограничиться пассивным несогласием. | ||
| + | |||
| + | Мы убеждены в абсолютной ценности человеческой жизни, в незыблемости прав и свобод личности. Режим Путина — угроза этим ценностям. Наша задача — обьединить все силы для сопротивления ей. | ||
| + | |||
| + | Эту войну начали не россияне, а обезумевший диктатор. И наш гражданский долг — сделать всё, чтобы её остановить. | ||
| + | |||
| + | ''Антивоенный комитет России'' | ||
| + | |-style="font-size: 16px;" | ||
| + | |Распространяйте правду о текущих событиях, оберегайте от пропаганды своих друзей и близких. Изменение общественного восприятия войны - ключ к её завершению. | ||
| + | |-style="font-size: 16px;" | ||
| + | |[https://meduza.io/ meduza.io], [https://www.youtube.com/c/popularpolitics/videos Популярная политика], [https://novayagazeta.ru/ Новая газета], [https://zona.media/ zona.media], [https://www.youtube.com/c/MackNack/videos Майкл Наки]. | ||
| + | |} | ||
| + | |||
Существует класс эволюционных алгоритмов, основывающихся на [[Эволюционные алгоритмы многокритериальной оптимизации, основанные на индикаторах. Гиперобъем|индикаторах]] для решения задачи [[Задача многокритериальной оптимизации. Multiobjectivization|многокритериальной оптимизации]]. | Существует класс эволюционных алгоритмов, основывающихся на [[Эволюционные алгоритмы многокритериальной оптимизации, основанные на индикаторах. Гиперобъем|индикаторах]] для решения задачи [[Задача многокритериальной оптимизации. Multiobjectivization|многокритериальной оптимизации]]. | ||
В данной статье приводится доказательство правомерности использования индикатора [[Эволюционные алгоритмы многокритериальной оптимизации, основанные на индикаторах. Гиперобъем#Гиперобъем|гиперобъема]] в качестве максимизируемого значения из работы <ref>[http://www.mpi-inf.mpg.de/homepage/tfried/paper/2010GECCO_Hyp.pdf Friedrich T., Bringmann K. - The Maximum Hypervolume Set Yields Near-optimal Approximation]</ref>. | В данной статье приводится доказательство правомерности использования индикатора [[Эволюционные алгоритмы многокритериальной оптимизации, основанные на индикаторах. Гиперобъем#Гиперобъем|гиперобъема]] в качестве максимизируемого значения из работы <ref>[http://www.mpi-inf.mpg.de/homepage/tfried/paper/2010GECCO_Hyp.pdf Friedrich T., Bringmann K. - The Maximum Hypervolume Set Yields Near-optimal Approximation]</ref>. | ||
Версия 08:46, 1 сентября 2022
| НЕТ ВОЙНЕ |
|
24 февраля 2022 года российское руководство во главе с Владимиром Путиным развязало агрессивную войну против Украины. В глазах всего мира это военное преступление совершено от лица всей страны, всех россиян. Будучи гражданами Российской Федерации, мы против своей воли оказались ответственными за нарушение международного права, военное вторжение и массовую гибель людей. Чудовищность совершенного преступления не оставляет возможности промолчать или ограничиться пассивным несогласием. Мы убеждены в абсолютной ценности человеческой жизни, в незыблемости прав и свобод личности. Режим Путина — угроза этим ценностям. Наша задача — обьединить все силы для сопротивления ей. Эту войну начали не россияне, а обезумевший диктатор. И наш гражданский долг — сделать всё, чтобы её остановить. Антивоенный комитет России |
| Распространяйте правду о текущих событиях, оберегайте от пропаганды своих друзей и близких. Изменение общественного восприятия войны - ключ к её завершению. |
| meduza.io, Популярная политика, Новая газета, zona.media, Майкл Наки. |
Существует класс эволюционных алгоритмов, основывающихся на индикаторах для решения задачи многокритериальной оптимизации. В данной статье приводится доказательство правомерности использования индикатора гиперобъема в качестве максимизируемого значения из работы [1].
Содержание
Основные определения
| Определение: |
| Множество функций вида: , где убывает и обозначим через . |
Коэффициент апроксимации монотонно убывающих функций не зависит от масштабов отрезков и . Так как для фиксированных констант функция и имеет тот же коэффициент аппроксимации. Однако, коэффициент аппроксимации зависит от значений и .
| Определение: |
| Фиксируем . Для фиксированного отрезка будем называть кортеж , такой что — множеством-решением. Множество таких решений будем обозначать . |
| Определение: |
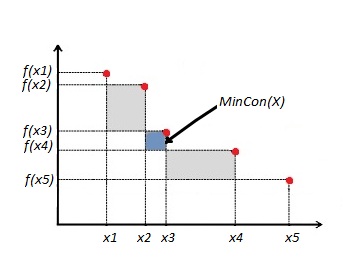
| Пусть и . Тогда вкладом -й точки в гиперобъем решения называется
. Минимальным вкладом в гиперобъем множества-решения называется . |
Далее будем рассматривать только монотонно убывающие, полунепрерывные Парето-фронты. Условие полунепрерывности необходимо для того, чтобы существовало множество-решение, максимизирующее индикатор гиперобъема.
Рассмотрим оптимальный коэффициент апроксимации для данного Парето-фронта из точек и верхнюю границу коэффициента аппроксимации для множества из точек, максимизирующего значение индикатора гиперобъема , и докажем, что для количества точек они одинаковы, а именно равны .
Индикатор гиперобъема
| Утверждение (1): |
Пусть .
Тогда существует, не обязятельно единственное, множество-решение , которое максимизирует значение гиперобъема на |
Доказательство представлено в статье Эволюционные алгоритмы многокритериальной оптимизации, основанные на индикаторах. Гиперобъем
Нахождение лучшего коэффициента аппроксимации
В статье Эволюционные алгоритмы многокритериальной оптимизации, основанные на индикаторах. Гиперобъем представленно доказательство верхней границы оптимального коэффицента апроксимации: = .
Нахождение коэффициента аппроксимации множества-решения максимизируюшего гиперобъем
| Утверждение (2): |
Пусть и .
Тогда минимальный вклад данного множества-решения: |
|
Исходя из определения минимальный вклад в гиперобъем множества равен минимуму из всевозможных площадей прямоугольников, образующихся между точками множества-решения и их значениями. Примеры образующихся прямоугольников заштрихованы на рисунке ниже Пусть — длины сторон соответствующего прямоугольника, тогда: для всех Это означает:
и поэтому: Так как среднее гармоническое не больше среднего арифметического: |
Далее необходимо посчитать коэффициент аппроксимации для «внутренних» () и «внешних» точек ( или ).
| Теорема (1): |
Пусть . Любое множество-решение достигает аппроксимации всех внутренних точек. |
| Доказательство: |
|
Допустим, что существует , который не аппроксимируется . Пусть , тогда . Известно, что . После подстановки получим (1). Применив утверждение (2), получим: для всех (2) для всех (3) Таким образом, . Т.к. монотонно убывает, а монотонно возрастает, то максимальное значение достигается при равенстве обоих членов: . Получим верхнюю оценку для : . Вышесказанное верно для . Для из (1) и (3) следует, что , что невозможно по условию теоремы. Для по (1) и (2) , что тоже невозможно по условию теоремы. |
| Теорема (2): |
Пусть . И является точкой отсчета. Каждое множество-решение достигает аппроксимации всех точек с и аппроксимации всех точек с . |
| Доказательство: |
| Доказательство производится c использованием ранее доказанного утверждения о . |
Из теоремы (1) и теоремы (2) выводятся следующие следствия:
| Утверждение (Следствие 1): |
Пусть , и является точкой отсчета. Тогда:
|
| Утверждение (Следствие 2): |
Пусть . И является точкой отсчета. Тогда если
или , выполняется следующее неравенство = , то есть = |
что и требовалось доказать.
Примечание
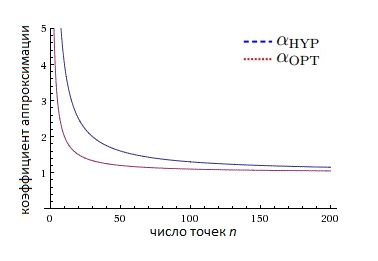
Конечно, зависимость от и в аппроксимационном коэффициенте оптимального множества решения меньше, чем в аппроксимационном коэффициенте для множества, максимизирующего гиперобъем. Однако, полученная граница для коэффициента аппроксимации является верхней. На рисунке ниже можно увидеть пример поведения данных значений для класса функций , .