Поиск k-ой порядковой статистики за линейное время — различия между версиями
м (rollbackEdits.php mass rollback) |
|||
| Строка 1: | Строка 1: | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
Алгоритм был разработан Мануэлем Блюмом (Manuel Blum), Робертом Флойдом (Robert Floyd), Воганом Рональдом Праттом (Vaughan Ronald Pratt), Роном Ривестом (Ron Rivest), Робертом Тарьяном (Robert Tarjan). | Алгоритм был разработан Мануэлем Блюмом (Manuel Blum), Робертом Флойдом (Robert Floyd), Воганом Рональдом Праттом (Vaughan Ronald Pratt), Роном Ривестом (Ron Rivest), Робертом Тарьяном (Robert Tarjan). | ||
==Идея алгоритма== | ==Идея алгоритма== | ||
Текущая версия на 19:05, 4 сентября 2022
Алгоритм был разработан Мануэлем Блюмом (Manuel Blum), Робертом Флойдом (Robert Floyd), Воганом Рональдом Праттом (Vaughan Ronald Pratt), Роном Ривестом (Ron Rivest), Робертом Тарьяном (Robert Tarjan).
Содержание
Идея алгоритма
Этот алгоритм является модификацией алгоритма поиска k-ой порядковой статистики. Важное отличие заключается в том, что время работы алгоритма в наихудшем случае — , где — количество элементов в множестве. Главная идея алгоритма заключается в том, чтобы гарантировать хорошее разбиение массива. Алгоритм выбирает такой рассекающий элемент, что количество чисел, которые меньше рассекающего элемента, не менее . Элементов же больших опорного элемента, также не менее . Благодаря этому алгоритм работает за линейное время в любом случае.
Описание алгоритма
- Все элементов входного массива разбиваются на группы по пять элементов, в последней группе будет элементов. Эта группа может оказаться пустой при кратным .
- Сначала сортируется каждая группа, затем из каждой группы выбирается медиана.
- Путем рекурсивного вызова шага определяется медиана из множества медиан (верхняя медиана в случае чётного количества), найденных на втором шаге. Найденный элемент массива используется как рассекающий (за обозначим его индекс).
- Массив делится относительно рассекающего элемента .
- Если , то возвращается значение . Иначе запускается рекурсивно поиск элемента в одной из частей массива: -ой статистики в левой части при или -ой статистики в правой части при
Пример работы алгоритма
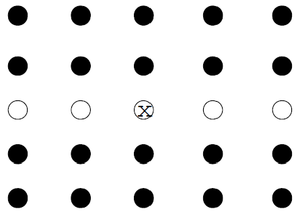
Рассмотрим работу алгоритма на массиве из элементов, обозначенных кружками.
На вход подается массив, разобьем элементы на группы по 5 элементов. Отсортируем элементы каждой группы и выберем медианы. Полученные медианы групп отмечены белыми кружками.
Рекурсивно вызовемся от медиан групп и получим рассекающий элемент. На рисунке он обозначен белым кружком, внутри которого изображен символ .
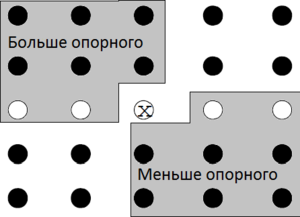
На рисунке обозначены закрашенные области, в левом верхнем и в правом нижнем углах. В эти области попали все элементы, которые точно меньше или больше рассекающего элемента, соответственно. В каждой области по элементов, всего же в массиве , то есть мы получили хорошее (то есть соответствующее нашему утверждению) разбиение массива относительно опорного элемента, так как . Теперь докажем, что алгоритм также хорошо выбирает опорный элемент и в общем случае.
Cначала определим нижнюю границу для количества элементов, превышающих по величине рассекающий элемент . В общем случае как минимум половина медиан, найденных на втором шаге, больше или равны медианы медиан . Таким образом, как минимум групп содержат по превышающих величину , за исключение группы, в которой меньше элементов и ещё одной группы, содержащей сам элемент . Таким образом получаем, что количество элементов больших , не менее .
Проведя аналогичные рассуждения для элементов, которые меньше по величине, чем рассекающий элемент , мы получим, что как минимум меньше, чем элемент . Теперь проведем анализ времени работы алгоритма.
Анализ времени работы алгоритма
Пусть — время работы алгоритма для элементов, тогда оно не больше, чем сумма:
- времени работы на сортировку групп и разбиение по рассекающему элементу, то есть ;
- времени работы для поиска медианы медиан, то есть ;
- времени работы для поиска -го элемента в одной из двух частей массива, то есть , где — количество элементов в этой части. Но не превосходит , так как чисел, меньших рассекающего элемента, не менее — это медиан, меньших медианы медиан, плюс не менее элементов, меньших этих медиан. С другой стороны, чисел, больших рассекающего элемента, так же не менее , следовательно , то есть в худшем случае .
Тогда получаем, что
Покажем, что для всех выполняется неравенство .
Докажем по индукции:
- Предположим, что наше неравенство выполняется при малых , для некоторой достаточно большой константы .
- Тогда, по предположению индукции, и , тогда
Так как , то время работы алгоритма
Источники инфомации
- Кормен, Т., Лейзерсон, Ч., Ривест, Р., Штайн, К. Алгоритмы: построение и анализ — Вильямс, 2013. — 1328 с. — ISBN 978-5-8459-1794-2
- Wikipedia — Selection algorithm