Эволюционные алгоритмы поиска эйлерова цикла в графе — различия между версиями

Текущая версия на 19:05, 4 сентября 2022

Содержание

1 Введение
2 Постановка задачи
3 Обзор методов
4 Алгоритм
5 Литература

Введение

Способ нахождения эйлерова цикла, описанный в данной статье, является примером применения эволюционных алгоритмов на практике. Мы опишем вариант построения, время работы которого [math]O(m \cdot \log m )[/math]^[1] (до недавнего времени лучшим считался результат [math]O(m^2 \cdot \log m)[/math])^[2]. При этом оптимальный (не эволюционный) алгоритм работает за [math]O(m)[/math]. Здесь и далее [math]m[/math] — количество ребер в графе. Время работы эволюционных алгоритмов измеряется в количестве вычислений функции приспособленности, а время оптимального алгоритма — в элементарных операциях.

После обзора предыдущих методов опишем представление графа, затем то, как устроена функция приспособленности и операция мутации, а потом адаптируем RLS и (1+1) EA стратегии для нашего случая.

Постановка задачи

Определение:

Эйлеров цикл в графе — это цикл, проходящий по всем рёбрам графа ровно по одному разу.

Задача — для заданного графа найти такой цикл. Здесь и далее рассматриваем неориентированный связный граф. Заметим, что это возможно тогда и только тогда, когда граф связный и степень каждой его вершины четна (для неориентированного графа).

Обзор методов

Перестановка ребер

Пусть для графа [math]G[/math] задан набор всех его ребер [math](e_1, e_2, \dots e_m)[/math]. На каждом шаге два случайно выбранных ребра меняются местами. Функция приспособленности — длина максимального пути в множестве ребер. Алгорим работает за экспоненциальное от количества ребер время ^[3].

Jump-оператор

Jump-оператор работает следующим образом. Для набора ребер [math](e_1, e_2, \dots e_m)[/math] оператор [math]jump(i,j)[/math] передвигает [math]i[/math]-й элемент на позицию [math]j[/math] и циклически сдвигает ребра между позициями [math]i[/math] и [math]j[/math] влево (если [math]i \gt j[/math] то вправо) . Таким образом, набор [math](e_1, e_2, \dots e_m)[/math] превратится в . Алгоритм с использованием jump-оператора работает за [math]O(m^5)[/math] ^[3], где [math]m[/math] — количество ребер в графе.

Улучшенный jump-оператор

Лучших результатов можно достичь, если использовать только операции вида [math]jump(i, 1)[/math]. Тогда время работы алгоритма будет [math]O(m^3)[/math] ^[4].

Алгоритм

Представление графа

Пусть [math]G[/math] — неориентированный связный граф, [math]V[/math] — множество его вершин, [math]E[/math] — множество ребер; всего вершин [math]n[/math], а ребер [math]m[/math] . Будем хранить ребра в виде списков смежности. Пусть [math]L_v[/math] — множество вершин, соединенных с [math]v[/math] ребром, [math]L[/math] — множество всех [math]L_v[/math]. Для каждой вершины [math]v[/math] введем также множество [math]M_v[/math], хранящее в себе неупорядоченные пары вершин из [math]L_v[/math]. Обозначим через [math]M[/math] множество всех [math]M_v[/math]. Таким образом, если для всех вершин [math]v[/math] вершины из [math]L_v[/math] разбиты на пары в [math]M_v[/math], то с точностью до первого ребра на [math]G[/math] задан порядок обхода: пара [math](u,w)[/math] в [math]L_v[/math] означает, что придя из [math]u[/math] далее нужно идти в [math]w[/math] (или наоборот).

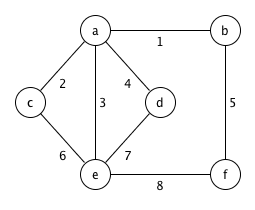
Рассмотрим пример.

Эйлерову циклу, проходящему по ребрам (2, 6, 7, 4, 3, 8, 5, 1) будет соответстовать множество [math]M[/math] такого вида:

[math]M_a = {(b,c); (e,d)}[/math]

[math]M_b = {(a,f)}[/math]

[math]M_c = {(a,e)}[/math]

[math]M_d = {(a,e)}[/math]

[math]M_e = {(f,a); (c,d)}[/math]

[math]M_f = {(e,b)}[/math]

Функция приспособленности

Функция приспособленности для эволюционного алгоритма поиска эйлерова цикла в графе выглядит так:

[math]f(M) = m - |M| + k[/math], где

[math]m[/math] — количество ребер в графе;

[math]|M|[/math] — размер множества [math]M[/math];

[math]k[/math] — количество путей (в том числе циклов) в [math]M[/math].

Операция мутации

Операция мутации вводится для двух вершин [math]u[/math] и [math]w[/math] из [math]L_v[/math]. Как их выбрать описано в следующем разделе. Происходит она так:

если [math]u=w[/math], то ничего не делаем;
если для [math]u[/math] и для [math]w[/math] нет пары, то добавляем к [math]M_v[/math] пару [math](u,w)[/math];
если [math]u[/math] и [math]w[/math] уже содержатся в [math]M_v[/math] как пара, то удалим ее;
если [math]u[/math] уже добавлена в паре с некоторой вершиной [math]p[/math], а [math]w[/math] не имеет пары, то удалим [math](u,p)[/math] из [math]M_v[/math] и добавим [math](u,w)[/math];
если [math]w[/math] уже добавлена в паре с некоторой вершиной [math]p[/math], а [math]u[/math] не имеет пары, то удалим [math](w,p)[/math] из [math]M_v[/math] и добавим [math](u,w)[/math];
если [math]u[/math] уже добавлена в паре с некоторой вершиной [math]p[/math], а [math]w[/math] уже добавлена в паре с некоторой [math]k[/math], то удалим [math](u,p)[/math] и [math](w,k)[/math] из [math]M_v[/math] и добавим [math](u,w)[/math] и [math](p,k)[/math];

Выбор вершин для мутации

Пусть [math]d(v)[/math] — степень вершины [math]v[/math] (количество ребер, которые из нее выходят), [math]d(G)[/math] — средняя степень среди вершин [math]G[/math], [math]\Delta G[/math] — максимальная степень среди вершин [math]G[/math], а . Есть три способа выбрать две вершины для мутации.

Ориентированный на вершины

Сначала случайно выбираем [math]v[/math] из [math]V[/math]. Затем случайно и независимо выбираем [math]u[/math] и [math]w[/math] из [math]L_v[/math]. Вероятность [math]p[/math] выбрать пару [math](u,w)[/math] в [math]L_v[/math] удовлетворяет соотношению:

Ориентированный на ребра

Выбираем случайно вершину [math]u[/math] из всех [math]2m[/math] вершин во всех списках [math]L[/math]. Пусть она оказалась в [math]L_v[/math]. Далее случайно выбираем [math]w[/math] из [math]L_v[/math]. Вероятность [math]p[/math] выбрать пару [math](u,w)[/math] в [math]L_v[/math] удовлетворяет соотношению:

Ориентированный на пары вершин

Выбираем случайно пару [math](u,w)[/math] из всех пар для всех [math]2m[/math] вершин во всех списках в [math]L[/math]. Пусть обе вершины присутствуют в [math]L_v[/math]. Тогда вероятность [math]p[/math] выбрать пару [math](u,w)[/math] в [math]L_v[/math] удовлетворяет соотношению:

Эти три случая эквивалентны в случае разреженного графа (в котором ). В общем случае и лучший результат достигается для способа, который ориентирован на вершины.

Стратегии RLS и (1+1) EA

Эволюционный алгоритм поиска эйлерова цикла в графе работает следующим образом. Размер популяции возьмем равным одному; представление графа, операция мутации и функция приспособленности будут такими, как описано выше. Начальное заполнение множества [math]M[/math] можно сделать случаным образом или оставить пустым.

Стратегия Randomized local search будет работать так: на каждом шаге к текущему индивиду (он один, так как в популяции только одна особь) применяется операция мутации. Если полученный индивид лучше текущего, он выбирается для дальнейшей работы, в противном случае ничего не происходит. Алгоритм работает до тех пор, пока функция приспособленности не минимизирована.

Псевдокод:

 Initialize(M)
 while (f(M) > 1) do
     M′:=φ(M) 
     if f(M′) ≤ f(M) 
         then M := M′

Стратегия (1+1) evolutionary algorithm в классическом варианте применяет операцию мутации к каждому биту [math]n[/math]-битной строки с вероятностью [math] \frac{1} {n}[/math]. В текущем алгоритме применять изменения можно только последовательно, поэтому просто делают операцию мутации несколько раз.

Псевдокод:

 Initialize(M) 
 while (f(M) > 1) do
     M′ :=M 
     for i := 0 to k do //k — некоторое число
         M′ := φ(M′) 
     if f(M′) ≤ f(M) 
         then M := M′

Время работы алгоритма

Лемма:

Пусть . Тогда множеству с функцией приспособленности соответствует не менее путей.

Доказательство:

Пусть соответствует путей. Тогда функция приспособленности будет , откуда

Теорема:

Ожидаемое время работы эволюционного алгоритма поиска эйлерова цикла в графе по RLS будет:

для стратегии, ориентированной на вершины;

для стратегии, ориентированной на ребра;

для стратегии, ориентированной на пары.

Доказательство:

Предположим, что значение функции приспособленности в данный момент [math]k[/math]. Тогда путей не менее [math]k/2[/math]. Если путь является циклом, то в нем есть хотя бы одна вершина, соединяющая данный путь с каким-то другим, то есть найдется пара [math](u, w)[/math], к которой можно применить мутацию и уменьшить количество путей. Если путь не является циклом, то так же найдется пара, при применении к которой мутации либо уменьшится количество путей, либо путь замкнется в цикл. Количество мутаций, которые уменьшают функцию приспособленности [math]\Omega(k)[/math]. Как следствие, вероятность выбрать подходящую пару [math]\Omega(q \cdot k)[/math], где [math]q[/math] — вероятность выбрать подходящую пару. Поэтому ожидаемое время достижения улучшения будет [math]O(\frac{1} {k \cdot q})[/math]. Изначально значение функции приспособленности не более [math]2m[/math]. Суммируя по всем [math]k[/math] без учета констант получаем:

Подствляя вместо различные для разных стратегий выбора пар вершин получаем требуемые оценки времени работы алгоритма.

Для случая, когда [math]M[/math] — разбиение графа на несколько циклов, время работы алгоритма для стратегии, ориентированной на ребра будет [math]O(m \cdot log \, m )[/math]. Получить такое разбриение можно разбив вершины во всех списках смежности на пары случайным образом.

Литература

↑ Doerr B., Johannsen D. Adjacency List Matchings - An Ideal Genotype for Cycle Covers. Proceeding GECCO '07 Proceedings of the 9th annual conference on Genetic and evolutionary computation, 1203-1210 (2007)
↑ B. Doerr, C. Klein, and T. Storch. Faster evolutionary algorithms by superior graph representation. In Proc. of the 2007 IEEE Symposium on Foundations of Computational Intelligence (FOCI), 245–250 (2007).
↑ ^3,0 ^3,1 F. Neumann. Expected runtimes of evolutionary algorithms for the Eulerian cycle problem. In Proc. of the 2004 IEEE Congress on Evolutionary Computation (CEC), 904–910 (2004).
↑ B. Doerr, N. Hebbinghaus, and F. Neumann. Speeding up evolutionary algorithms through restricted mutation operators. In Proc. of the 9th International Conference on Parallel Problem Solving From Nature (PPSN), volume 4193 of LNCS, 978–987 (2006).

[1] Doerr B., Johannsen D. Adjacency List Matchings - An Ideal Genotype for Cycle Covers. Proceeding GECCO '07 Proceedings of the 9th annual conference on Genetic and evolutionary computation, 1203-1210 (2007)

[2] B. Doerr, C. Klein, and T. Storch. Faster evolutionary algorithms by superior graph representation. In Proc. of the 2007 IEEE Symposium on Foundations of Computational Intelligence (FOCI), 245–250 (2007).

[Neumann-3] 3,0 ^3,1 F. Neumann. Expected runtimes of evolutionary algorithms for the Eulerian cycle problem. In Proc. of the 2004 IEEE Congress on Evolutionary Computation (CEC), 904–910 (2004).

[4] B. Doerr, N. Hebbinghaus, and F. Neumann. Speeding up evolutionary algorithms through restricted mutation operators. In Proc. of the 9th International Conference on Parallel Problem Solving From Nature (PPSN), volume 4193 of LNCS, 978–987 (2006).

[1]

[2]

[3]

[4]

@@ Строка 1: / Строка 1: @@
 === Введение ===
-Способ нахождения эйлерова цикла, описанный в данной статье, является примером применения эволюционных алгоритмов на практике. Мы опишем вариант построения, время работы которого <tex>O(m \cdot log \, m )</tex><ref>Doerr B., Johannsen D. Adjacency List Matchings - An Ideal Genotype for Cycle Covers. Proceeding GECCO '07 Proceedings of the 9th annual conference on Genetic and evolutionary computation, 1203-1210 (2007)</ref> (до недавнего времени лучшим считался результат <tex>O(m^2 \cdot log\,m)</tex>)<ref>B. Doerr, C. Klein, and T. Storch. Faster evolutionary algorithms by superior graph representation. In Proc. of the 2007 IEEE Symposium on Foundations of Computational Intelligence (FOCI), 245–250 (2007).</ref>. При этом оптимальный (не эволюционный) [[Алгоритм построения Эйлерова цикла|алгоритм]] работает за <tex>O(m)</tex>. Здесь и далее <tex>m</tex> — количество ребер в графе. Время работы эволюционных алгоритмов измеряется в количестве вычислений функции приспособленности, а время оптимального алгоритма — в итерациях.
+Способ нахождения эйлерова цикла, описанный в данной статье, является примером применения эволюционных алгоритмов на практике. Мы опишем вариант построения, время работы которого <tex>O(m \cdot \log m )</tex><ref>Doerr B., Johannsen D. Adjacency List Matchings - An Ideal Genotype for Cycle Covers. Proceeding GECCO '07 Proceedings of the 9th annual conference on Genetic and evolutionary computation, 1203-1210 (2007)</ref> (до недавнего времени лучшим считался результат <tex>O(m^2 \cdot \log m)</tex>)<ref>B. Doerr, C. Klein, and T. Storch. Faster evolutionary algorithms by superior graph representation. In Proc. of the 2007 IEEE Symposium on Foundations of Computational Intelligence (FOCI), 245–250 (2007).</ref>. При этом оптимальный (не эволюционный) [[Алгоритм построения Эйлерова цикла|алгоритм]] работает за <tex>O(m)</tex>. Здесь и далее <tex>m</tex> — количество ребер в графе. Время работы эволюционных алгоритмов измеряется в количестве вычислений функции приспособленности, а время оптимального алгоритма — в элементарных операциях.
 После обзора предыдущих методов опишем представление графа, затем то, как устроена функция приспособленности и операция мутации, а потом адаптируем RLS и (1+1) EA стратегии для нашего случая.
@@ Строка 12: / Строка 12: @@
 === Обзор методов ===
 ====Перестановка ребер ====
-Пусть для графа <tex>G</tex> задан набор всех его ребер <tex>(e_1, e_2, \dots e_m)</tex>. На каждом шаге два случайно выбранных ребра меняются местами. Функция приспособленности — длина максимального пути в множестве ребер. Алгорим работает за экспоненциальное от количества ребер время.
+Пусть для графа <tex>G</tex> задан набор всех его ребер <tex>(e_1, e_2, \dots e_m)</tex>. На каждом шаге два случайно выбранных ребра меняются местами. Функция приспособленности — длина максимального пути в множестве ребер. Алгорим работает за экспоненциальное от количества ребер время <ref name = "Neumann">F. Neumann. Expected runtimes of evolutionary algorithms for the Eulerian cycle problem. In Proc. of the 2004 IEEE Congress on Evolutionary Computation (CEC), 904–910 (2004).</ref>.
 ====Jump-оператор====
-Jump-оператор работает следующим образом. Для набора ребер <tex>(e_1, e_2, \dots e_m)</tex> оператор <tex>jump(i,j)</tex> передвигает <tex>i</tex>-й элемент на позицию <tex>j</tex> и циклически сдвигает ребра между позициями <tex>i</tex> и <tex>j</tex> влево (если <tex>i > j</tex> то вправо) .  Таким образом, набор <tex>(e_1, e_2, \dots e_m)</tex> превратится в <tex>(e_1, e_2, \dots e_{i-1}, e_{i+1}, \dots e_j, e_i, e_{j+1}, \dots e_m)</tex>. Алгоритм с использованием jump-оператора работает за <tex>O(m^5)</tex>, где <tex>m</tex> — количество ребер в графе.
+Jump-оператор работает следующим образом. Для набора ребер <tex>(e_1, e_2, \dots e_m)</tex> оператор <tex>jump(i,j)</tex> передвигает <tex>i</tex>-й элемент на позицию <tex>j</tex> и циклически сдвигает ребра между позициями <tex>i</tex> и <tex>j</tex> влево (если <tex>i > j</tex> то вправо) .  Таким образом, набор <tex>(e_1, e_2, \dots e_m)</tex> превратится в <tex>(e_1, e_2, \dots e_{i-1}, e_{i+1}, \dots e_j, e_i, e_{j+1}, \dots e_m)</tex>. Алгоритм с использованием jump-оператора работает за <tex>O(m^5)</tex> <ref name = "Neumann" />, где <tex>m</tex> — количество ребер в графе.
 ====Улучшенный jump-оператор====
-Лучших результатов можно достичь, если использовать только операции вида <tex>jump(i, 1)</tex>. Тогда время работы алгоритма будет <tex>O(m^3)</tex>.
+Лучших результатов можно достичь, если использовать только операции вида <tex>jump(i, 1)</tex>. Тогда время работы алгоритма будет <tex>O(m^3)</tex> <ref>B. Doerr, N. Hebbinghaus, and F. Neumann. Speeding up evolutionary algorithms through restricted mutation operators. In Proc. of the 9th International Conference on Parallel Problem Solving From Nature (PPSN), volume 4193 of LNCS, 978–987 (2006).</ref>.
 === Алгоритм ===
 ==== Представление графа ====
@@ Строка 22: / Строка 25: @@
 Рассмотрим пример.
-[[Файл:GraphMPinsky.jpg]]
+[[Файл:GraphMPinsky.png]]
+Эйлерову циклу, проходящему по ребрам (2, 6, 7, 4, 3, 8, 5, 1) будет соответстовать множество <tex>M</tex> такого вида:
+<tex>M_a = {(b,c); (e,d)}</tex>
+<tex>M_b = {(a,f)}</tex>
+<tex>M_c = {(a,e)}</tex>
+<tex>M_d = {(a,e)}</tex>
+<tex>M_e = {(f,a); (c,d)}</tex>
+<tex>M_f = {(e,b)}</tex>
 ==== Функция приспособленности ====
@@ Строка 71: / Строка 90: @@
 ==== Стратегии RLS и (1+1) EA ====
-Эволюционный алгоритм поиска эйлерова цикла в графе работает следующим образом. Размер популяции возьмем равным одному; представление графа, операция мутации и функция приспособленности будут такими, как описано выше. Начальное заполнение множества <tex>M</tex> можно сделать случаным образом или оставить пустым, на время работы алгоритма это не влияет.
+Эволюционный алгоритм поиска эйлерова цикла в графе работает следующим образом. Размер популяции возьмем равным одному; представление графа, операция мутации и функция приспособленности будут такими, как описано выше. Начальное заполнение множества <tex>M</tex> можно сделать случаным образом или оставить пустым.
 Стратегия Randomized local search будет работать так: на каждом шаге к текущему индивиду (он один, так как в популяции только одна особь) применяется операция мутации. Если полученный индивид лучше текущего, он выбирается для дальнейшей работы, в противном случае ничего не происходит. Алгоритм работает до тех пор, пока функция приспособленности не минимизирована.
@@ Строка 94: / Строка 113: @@
 ==== Время работы алгоритма ====
-Для RLS и (1+1) EA верны следующие оценки времени работы алгоритма:
+{{Лемма
+|statement=
+Пусть <tex>1 \le k \le 2m</tex>. Тогда множеству <tex>M</tex> с функцией приспособленности <tex>k</tex> соответствует не менее <tex>k/2</tex> путей.
+|proof=
+Пусть <tex>M</tex> соответствует <tex>x</tex> путей. Тогда функция приспособленности <tex>f</tex> будет <tex>f = k \le m - |M - x| + x = 2x</tex>, откуда <tex>x \ge k/2</tex>
+}}
+{{Теорема
+|statement=
+Ожидаемое время работы эволюционного алгоритма поиска эйлерова цикла в графе по RLS будет:
 <tex>O(\frac{\Delta(G)^2} {d(G)} \cdot m \cdot log \, m)</tex> для стратегии, ориентированной на вершины;
@@ Строка 101: / Строка 128: @@
 <tex>O(\delta d(G) \cdot m \cdot log \, m )</tex> для стратегии, ориентированной на пары.
+|proof=Предположим, что значение функции приспособленности в данный момент <tex>k</tex>. Тогда путей не менее <tex>k/2</tex>. Если путь является циклом, то в нем есть хотя бы одна вершина, соединяющая данный путь с каким-то другим, то есть найдется пара <tex>(u, w)</tex>, к которой можно применить мутацию и уменьшить количество путей. Если путь не является циклом, то так же найдется пара, при применении к которой мутации либо уменьшится количество путей, либо путь замкнется в цикл. Количество мутаций, которые уменьшают функцию приспособленности <tex>\Omega(k)</tex>. Как следствие, вероятность выбрать подходящую пару <tex>\Omega(q \cdot k)</tex>, где <tex>q</tex> — вероятность выбрать подходящую пару. Поэтому ожидаемое время достижения улучшения будет <tex>O(\frac{1} {k \cdot q})</tex>. Изначально значение функции приспособленности не более <tex>2m</tex>. Суммируя по всем <tex>k</tex> без учета констант получаем:
+<tex>\sum_{k=1}^{m}  \frac{1} {k \cdot q} = \frac{1} {q} \sum_{k=1} ^{m} \frac{1} {k} = O(\frac{1} {q}log \, m)</tex>
+Подствляя вместо <tex>q</tex> различные <tex>p</tex> для разных стратегий выбора пар вершин получаем требуемые оценки времени работы алгоритма.
+}}
+Для случая, когда <tex>M</tex> — разбиение графа на несколько циклов, время работы алгоритма для стратегии, ориентированной на ребра будет <tex>O(m \cdot log \, m )</tex>. Получить такое разбриение можно разбив вершины во всех списках смежности на пары случайным образом.
 === Литература ===
 <references/>