Гиперграфы — различия между версиями
Romanosov (обсуждение | вклад) м |
м (rollbackEdits.php mass rollback) |
||
| (не показано 19 промежуточных версий 4 участников) | |||
| Строка 1: | Строка 1: | ||
{{Определение | {{Определение | ||
| − | |definition = | + | |definition= |
| − | '''Гиперграфом''' <tex>H | + | '''Гиперграфом''' (англ. ''hypergraph'') <tex>H</tex> называют такую пару <tex>H = (X, E)</tex> , где <tex>X - </tex> множество вершин, а <tex>E -</tex> семейство подмножеств <tex>X</tex> , называемых '''гиперребрами''' (англ. ''hyperedges'') |
| + | }} | ||
| − | + | Обычные графы, у которых ребра могут соединять только две вершины, являются частным случаем гиперграфа, у которых все гиперребра содержат только две вершины. | |
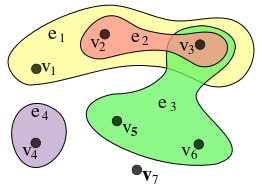
| − | <tex> | + | [[Файл:Hypergraph.jpg|thumb|450px|Рис. 1: Гиперграф с множеством вершин <tex>V = \{ v_1, v_2, v_3, v_4, v_5, v_6, v_7 \}</tex> и гиперребрами <tex>E = \{ \{ v_1, v_2, v_3 \} , \{ v_2, v_3 \} , \{ v_3, v_5, v_6 \} , \{ v_4 \} \}</tex>]] |
| − | |||
| − | + | ||
| + | ==Основные понятия гиперграфов== | ||
| + | |||
| + | {{Определение | ||
| + | |definition= | ||
| + | '''Путем''' (англ. ''path'') между двумя гиперребрами <tex>e_i</tex> и <tex>e_j</tex> гиперграфа <tex>H</tex> называется последовательность гиперребер <tex>e_{u_1}, e_{u_2} , \ldots ,e_{u_k}</tex> таких что : | ||
| + | # <tex>e_{u_1} = e_i </tex> и <tex>e_{u_k} = e_j</tex> | ||
| + | # <tex>\forall v: 1 \leqslant v \leqslant k-1, e_v \cap e_{v+1} \ne \emptyset</tex> | ||
| + | }} | ||
| + | |||
| + | {{Определение | ||
| + | |definition= | ||
| + | Гиперграф <tex>H</tex> называется '''связным''' (англ. ''connected'') тогда и только тогда, когда существует путь между каждой парой гиперребер. | ||
| + | }} | ||
| + | |||
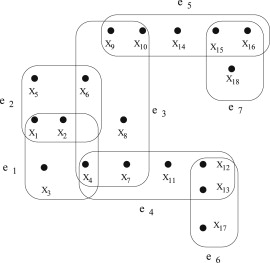
| + | [[Файл:Connected_hypergraph.jpg|thumb|450px|center|Рис. 2: Связный гиперграф]] | ||
| + | |||
| + | Пусть <tex>E - </tex> набор гиперребер, <tex>e_1</tex> и <tex>e_2 - </tex> элементы <tex>E</tex> и <tex>q = e_1 \cap e_2</tex>. | ||
| + | {{Определение | ||
| + | |definition= | ||
| + | <tex>q</tex> называется '''сочленением''' (англ. ''articulation'') <tex>E</tex> , если при его удалении из всех гиперребер <tex>E</tex>, множество разрывается. | ||
| + | }} | ||
| + | |||
| + | На рис.2 <tex>q = e_4 \cap e_6 = \{ x_{12}, x_{13}\}</tex> является сочленением <tex>E</tex>. | ||
| + | |||
| + | ==Матрица инцидентности == | ||
| + | |||
| + | Пусть дан гиперграф <tex>H = (X, E)</tex> , где <tex> X = \{ x_1, x_2, \ldots , x_n \}</tex> и <tex> E = \{ e_1, e_2, \ldots , e_m \}</tex>. Любой гиперграф может задаваться матрицей инцидентности (смотри [[Матрица_инцидентности_графа|матрицу инцидентности в обычном графе)]] <tex>A = (a_{ij}) </tex> размером <tex> n \times m</tex>, где | ||
| + | |||
| + | <tex> a_{ij} = \left \{ | ||
| + | \begin{array}{ll} | ||
| + | 0 & x_i \in e_j \\ | ||
| + | 1 & \mathrm{otherwise} | ||
| + | \end{array} | ||
| + | \right. | ||
| + | </tex> | ||
| + | |||
| + | Так например, для гиперграфа на рис.1 мы можем построить матрицу инцидентности по таблице отношения принодлежности вершины к гиперребру: | ||
| + | |||
| + | {| class="wikitable" align="left" style="color: black; background-color:#ffffcc;" cellpadding="10" | ||
| + | |+ | ||
| + | ! | ||
| + | !<tex>e_1</tex> | ||
| + | !<tex>e_2</tex> | ||
| + | !<tex>e_3</tex> | ||
| + | !<tex>e_4</tex> | ||
| + | |-align="center" | ||
| + | !<tex>v_1</tex> | ||
| + | |✓|||| || | ||
| + | |-align="center" | ||
| + | !<tex>v_2</tex> | ||
| + | |✓||✓|| || | ||
| + | |-align="center" | ||
| + | !<tex>v_3</tex> | ||
| + | |✓||✓||✓|| | ||
| + | |-align="center" | ||
| + | !<tex>v_4</tex> | ||
| + | | |||| ||✓ | ||
| + | |-align="center" | ||
| + | !<tex>v_5</tex> | ||
| + | |||||✓|| | ||
| + | |-align="center" | ||
| + | !<tex>v_6</tex> | ||
| + | |||||✓|| | ||
| + | |-align="center" | ||
| + | !<tex>v_7</tex> | ||
| + | ||||||| | ||
| + | |} | ||
| + | |||
| + | |||
| + | <tex> A = </tex> | ||
| + | <tex>\begin{pmatrix} | ||
| + | 1 & 0 & 0 & 0\\ | ||
| + | 1 & 1 & 0 & 0\\ | ||
| + | 1 & 1 & 1 & 0\\ | ||
| + | 0 & 0 & 0 & 1\\ | ||
| + | 0 & 0 & 1 & 0\\ | ||
| + | 0 & 0 & 1 & 0\\ | ||
| + | 0 & 0 & 0 & 0\\ | ||
| + | \end{pmatrix}</tex> | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | ==Цикл в гиперграфе== | ||
| + | |||
| + | {{Определение | ||
| + | |definition= | ||
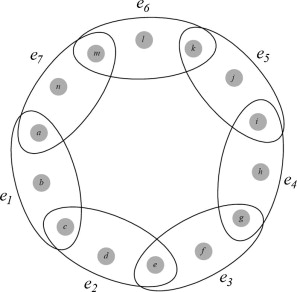
| + | '''Простым циклом''' длины <tex>s</tex> в гиперграфе <tex>H = (V, E)</tex> называется последовательность <tex>( A_0, v_0, A_1, \ldots , A_{s - 1}, v_{s - 1}, A_s)</tex> , где <tex>A_0 , \ldots , A_{s - 1} -</tex> различные ребра <tex>H</tex> , ребро <tex>A_s</tex> совпадает с <tex>A_0</tex> , а <tex>v_0, \ldots , v_{s - 1} -</tex> различные вершины <tex>H</tex> , причем <tex>v_i \in A_i \cap A_{i+1}</tex> для всех <tex> i = 0, \ldots , s - 1</tex>. | ||
| + | }} | ||
| + | |||
| + | [[Файл:Cycle_hyper.jpg|thumb|450px|center|Рис. 3: Простейший случай цикла в гиперграфе]] | ||
| + | |||
| + | |||
| + | Универсальным способом задания гиперграфа является кенигово представление. | ||
| + | |||
| + | {{Определение | ||
| + | |definition= | ||
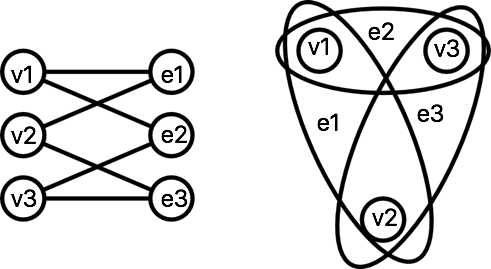
| + | '''Кенигово представление''' гиперграфа <tex> H = (V, E) -</tex> обыкновенный двудольный граф '''<tex>K(H)</tex>''' , отражающий отношение инцидентности различных элементов гиперграфа, с множеством вершин <tex>V \cup E </tex> и долями <tex>V, E</tex>. | ||
| + | }} | ||
| + | |||
| + | Первым, кто дал определение ацикличности гипергафа является Клауд Берж: | ||
| + | |||
| + | {{Теорема | ||
| + | |statement= | ||
| + | Гиперграф <tex>H</tex> не содержит циклов в том случае, если его кенигово представление <tex>-</tex> ацикличный граф, сожержит в противном случае. | ||
| + | }} | ||
| + | |||
| + | Таким образом, если у нас есть цикл в графе кенигова представления, значит и сам гиперграф имеет цикл. | ||
| + | |||
| + | [[Файл:Cycle_example.png|thumb|center|500px|Рис. 4: Пример гиперграфа, содержащего цикл]] | ||
| + | |||
| + | ===Алгоритм нахождения цикла в гиперграфе=== | ||
| + | |||
| + | Поскольку гиперграф может задаваться кениговым представлением, тогда произведём серию поисков в глубину в двудольном графе. Т.е. из каждой вершины, в которую мы ещё ни разу не приходили, запустим поиск в глубину, который при входе в вершину будет красить её в серый цвет, а при выходе - в чёрный. И если поиск в глубину пытается пойти в серую вершину, то это означает, что мы нашли цикл (если граф неориентированный, то случаи, когда поиск в глубину из какой-то вершины пытается пойти в предка, не считаются). | ||
| + | |||
| + | ==Ацикличность гиперграфов== | ||
| + | |||
| + | {{Определение | ||
| + | |definition= | ||
| + | '''Редукцией''' (англ. ''reduction'') гиперграфа <tex>H = (V, E)</tex> называется такой гиперграф <tex>H' = (V, E')</tex> , который получается из исходного путем удаления всех гиперребер, которые полностью содержатся в других гиперреберах. | ||
| + | }} | ||
| + | |||
| + | {{Определение | ||
| + | |definition= | ||
| + | Гиперграф называется '''уменьшенным''' (англ. ''reduced'') , если он эквивалентен своей редукции, то есть не имеет гиперребер внутри других гиперребер. | ||
}} | }} | ||
| − | |||
| − | |||
| − | + | Пусть <tex>M - </tex> множество вершин гиперграфа <tex>H = (V, E)</tex>. Множество '''частичных ребер''' (англ. ''partial edges''), порожденных множеством <tex>M</tex>, определяется как множество, полученное путем пересечения гиперребер из множества <tex>E</tex> с <tex>M</tex>. Таким образом, получаем множество : <tex> \{ e \cap M : e \in E \} - \{ \emptyset \} </tex> и берем его редукцию. | |
| − | <tex> | + | |
| + | Множество частичных ребер, порожденное из гиперграфа <tex>H</tex> множеством <tex>M</tex>, называется '''вершинно-порожденным''' (англ. ''node-generated'') множеством частичных ребер. | ||
| + | |||
| + | {{Определение | ||
| + | |definition= | ||
| + | '''Блоком''' (англ. ''block'') уменьшенного гиперграфа называется связное, вершинно - порожденное множество частичных ребер без сочленения. | ||
| + | }} | ||
| + | |||
| + | {{Определение | ||
| + | |definition= | ||
| + | Множество частичных ребер называется '''тривиальным''' (англ. ''trivial''), если оно содержит одно гиперребро. | ||
| + | }} | ||
| + | |||
| + | {{Определение | ||
| + | |definition= | ||
| + | Уменьшенный гиперграф называется '''<tex> \alpha </tex> - ацикличным''' (англ. ''<tex> \alpha </tex>-acyclity'') , если всего его блоки тривиальны, иначе называют '''<tex> \alpha </tex>-цикличным''' (англ. ''<tex> \alpha</tex>-cyclity''). | ||
| + | }} | ||
| + | |||
| + | ''Пример'' | ||
| + | |||
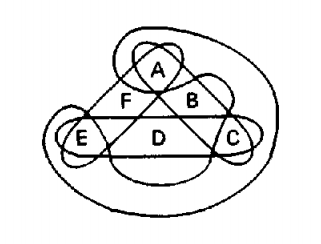
| + | [[Файл:Alpha-acyclity-1.png|thumb|left|500px|Рис. 5: <tex> \alpha</tex>-ацикличный гиперграф]] | ||
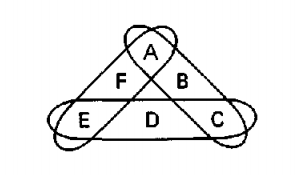
| + | [[Файл:Alpha-acyclity-2.png|thumb|center|500px|Рис. 6: Подмножество гиперребер <tex> \{ ABC, CDE, EFA\} </tex>]] | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | Очень просто проверить что на рис. 3 представлен <tex> \alpha </tex>-ацикличный гиперграф. Он содержит четыре гиперребра <tex>- ABC, CDE, EFA, ACE</tex>. Сочленение для всего множества гиперребер является <tex> ABC \cap ACE = AC </tex> , так как после удаления вершин <tex>A</tex> и <tex>C</tex> гиперграф не будет связным (вершина <tex>B</tex> не будет ни с кем соединена). Заметим, что на рис. 6 подмножетсво гиперребер <tex>\{ ABC, CDE, EFA \}</tex> не имеет сочленения. Однако, это множество не является вершинно - порожденным , таким образом, нет никаких противоречий с предположением, что гиперграф на рис. 5 является <tex> \alpha </tex>-ацикличным. | ||
| + | |||
| + | |||
| + | Заметим, что <tex> \alpha </tex>-ацикличность имеет одно нелогичное свойство: при добавлении гиперребер к <tex> \alpha </tex>-цикличному гиперграфу он может стать <tex> \alpha </tex>-ацикличным (например, при добавлении гиперребра, которое охватывает все вершины, всегда будет делать гиперграф <tex> \alpha </tex>-ацикличным). Из-за этого свойства было введено более строгое определение, называемое <tex> \beta </tex>-ацикличностью. | ||
| + | |||
| + | {{Определение | ||
| + | |definition= | ||
| + | Гиперграф <tex>H = (V, E) </tex> является '''<tex> \beta </tex>-ацикличным''' (англ. ''<tex> \beta </tex>-acyclity'') , если все его подгиперграфы <tex> \alpha </tex>-ацикличны. | ||
| + | }} | ||
| + | |||
| + | Так например гиперграф на рис. 5 является <tex> \alpha </tex>-ацикличным, но не является <tex> \beta </tex>-ацикличным, так как его подгиперграф на рис. 6 является <tex> \alpha </tex>-цикличным. | ||
| + | |||
| + | == См. также == | ||
| + | * [[Основные_определения_теории_графов|Основные определения теории графов]] | ||
| + | |||
| + | == Источники информации == | ||
| + | * [https://en.wikipedia.org/wiki/Claude_Berge wikipedia.com — Клауд Берж] | ||
| + | * [https://en.wikipedia.org/wiki/Hypergraph wikipedia.com — Гиперграфы] | ||
| + | * [http://www.sciencedirect.com/science/article/pii/S0012365X09003446?np=y sciencedirect.com — Ацикличность в гиперграфах] | ||
| + | |||
| + | [[Категория:Дискретная математика и алгоритмы]] | ||
| + | [[Категория:Основные определения теории графов]] | ||
Текущая версия на 19:07, 4 сентября 2022
| Определение: |
| Гиперграфом (англ. hypergraph) называют такую пару , где множество вершин, а семейство подмножеств , называемых гиперребрами (англ. hyperedges) |
Обычные графы, у которых ребра могут соединять только две вершины, являются частным случаем гиперграфа, у которых все гиперребра содержат только две вершины.
Содержание
Основные понятия гиперграфов
| Определение: |
Путем (англ. path) между двумя гиперребрами и гиперграфа называется последовательность гиперребер таких что :
|
| Определение: |
| Гиперграф называется связным (англ. connected) тогда и только тогда, когда существует путь между каждой парой гиперребер. |
Пусть набор гиперребер, и элементы и .
| Определение: |
| называется сочленением (англ. articulation) , если при его удалении из всех гиперребер , множество разрывается. |
На рис.2 является сочленением .
Матрица инцидентности
Пусть дан гиперграф , где и . Любой гиперграф может задаваться матрицей инцидентности (смотри матрицу инцидентности в обычном графе) размером , где
Так например, для гиперграфа на рис.1 мы можем построить матрицу инцидентности по таблице отношения принодлежности вершины к гиперребру:
| ✓ | ||||
| ✓ | ✓ | |||
| ✓ | ✓ | ✓ | ||
| ✓ | ||||
| ✓ | ||||
| ✓ | ||||
Цикл в гиперграфе
| Определение: |
| Простым циклом длины в гиперграфе называется последовательность , где различные ребра , ребро совпадает с , а различные вершины , причем для всех . |
Универсальным способом задания гиперграфа является кенигово представление.
| Определение: |
| Кенигово представление гиперграфа обыкновенный двудольный граф , отражающий отношение инцидентности различных элементов гиперграфа, с множеством вершин и долями . |
Первым, кто дал определение ацикличности гипергафа является Клауд Берж:
| Теорема: |
Гиперграф не содержит циклов в том случае, если его кенигово представление ацикличный граф, сожержит в противном случае. |
Таким образом, если у нас есть цикл в графе кенигова представления, значит и сам гиперграф имеет цикл.
Алгоритм нахождения цикла в гиперграфе
Поскольку гиперграф может задаваться кениговым представлением, тогда произведём серию поисков в глубину в двудольном графе. Т.е. из каждой вершины, в которую мы ещё ни разу не приходили, запустим поиск в глубину, который при входе в вершину будет красить её в серый цвет, а при выходе - в чёрный. И если поиск в глубину пытается пойти в серую вершину, то это означает, что мы нашли цикл (если граф неориентированный, то случаи, когда поиск в глубину из какой-то вершины пытается пойти в предка, не считаются).
Ацикличность гиперграфов
| Определение: |
| Редукцией (англ. reduction) гиперграфа называется такой гиперграф , который получается из исходного путем удаления всех гиперребер, которые полностью содержатся в других гиперреберах. |
| Определение: |
| Гиперграф называется уменьшенным (англ. reduced) , если он эквивалентен своей редукции, то есть не имеет гиперребер внутри других гиперребер. |
Пусть множество вершин гиперграфа . Множество частичных ребер (англ. partial edges), порожденных множеством , определяется как множество, полученное путем пересечения гиперребер из множества с . Таким образом, получаем множество : и берем его редукцию.
Множество частичных ребер, порожденное из гиперграфа множеством , называется вершинно-порожденным (англ. node-generated) множеством частичных ребер.
| Определение: |
| Блоком (англ. block) уменьшенного гиперграфа называется связное, вершинно - порожденное множество частичных ребер без сочленения. |
| Определение: |
| Множество частичных ребер называется тривиальным (англ. trivial), если оно содержит одно гиперребро. |
| Определение: |
| Уменьшенный гиперграф называется - ацикличным (англ. -acyclity) , если всего его блоки тривиальны, иначе называют -цикличным (англ. -cyclity). |
Пример
Очень просто проверить что на рис. 3 представлен -ацикличный гиперграф. Он содержит четыре гиперребра . Сочленение для всего множества гиперребер является , так как после удаления вершин и гиперграф не будет связным (вершина не будет ни с кем соединена). Заметим, что на рис. 6 подмножетсво гиперребер не имеет сочленения. Однако, это множество не является вершинно - порожденным , таким образом, нет никаких противоречий с предположением, что гиперграф на рис. 5 является -ацикличным.
Заметим, что -ацикличность имеет одно нелогичное свойство: при добавлении гиперребер к -цикличному гиперграфу он может стать -ацикличным (например, при добавлении гиперребра, которое охватывает все вершины, всегда будет делать гиперграф -ацикличным). Из-за этого свойства было введено более строгое определение, называемое -ацикличностью.
| Определение: |
| Гиперграф является -ацикличным (англ. -acyclity) , если все его подгиперграфы -ацикличны. |
Так например гиперграф на рис. 5 является -ацикличным, но не является -ацикличным, так как его подгиперграф на рис. 6 является -цикличным.