Рёберное ядро — различия между версиями
Artom32 (обсуждение | вклад) |
м (rollbackEdits.php mass rollback) |
||
| (не показано 56 промежуточных версий 7 участников) | |||
| Строка 1: | Строка 1: | ||
{{Определение| | {{Определение| | ||
definition= | definition= | ||
| − | '''Рёберное ядро''' <tex>C_1(G)</tex> графа <tex>G</tex> {{---}} это подграф графа <tex>G</tex>, порожденный объединением таких независимых множеств <tex>Y \subset E(G)</tex>, что <tex>|Y| = \alpha_{0}(G)</tex>, где <tex>\alpha_{0}(G)</tex> {{---}} число вершинного покрытия. | + | '''Рёберное ядро''' (англ. ''core'') <tex>C_1(G)</tex> графа <tex>G</tex> {{---}} это подграф [[Основные определения теории графов#finite graph|графа]] <tex>G</tex>, порожденный объединением таких независимых множеств <tex>Y \subset E(G)</tex>, что <tex>|Y| = \alpha_{0}(G)</tex>, где <tex>\alpha_{0}(G)</tex> {{---}} число вершинного покрытия. |
}} | }} | ||
| + | |||
{{Определение| | {{Определение| | ||
| − | definition= | + | definition= |
| − | '''Вершинным покрытием''' графа <tex>G</tex> называется такое множество <tex>V</tex> его вершин, что у любого ребра в <tex>G</tex> хотя бы одна из вершин лежит в <tex>V</tex>. | + | Множество [[Основные определения теории графов#def_graph_edge_1|ребер]] (вершин) называется '''независимым''' (англ. ''independent''), если никакие его два элемента не смежны. |
| + | }} | ||
| + | {{Определение | ||
| + | |id=def_3 | ||
| + | |definition= | ||
| + | '''Вершинным покрытием''' (англ. ''vertex cover'') графа <tex>G</tex> называется такое множество <tex>V</tex> его вершин, что у любого ребра в <tex>G</tex> хотя бы одна из вершин лежит в <tex>V</tex>. | ||
}} | }} | ||
{{Определение| | {{Определение| | ||
definition= | definition= | ||
| − | ''' | + | '''Числом вершинного покрытия''' (англ. ''point-covering number'') называется число вершин в наименьшем вершинном покрытии графа <tex>G</tex>. |
}} | }} | ||
==Критерий существования реберного ядра== | ==Критерий существования реберного ядра== | ||
{{Определение| | {{Определение| | ||
definition= | definition= | ||
| − | Наименьшее вершинное покрытие M графа G с множеством | + | Наименьшее вершинное покрытие <tex>M</tex> графа <tex>G</tex> с множеством вершин <tex>V</tex> называется '''внешним''' (англ. ''external vertex cover''), если для любого подмножества <tex>M' \subseteq M</tex> выполняется неравенство <tex>|M'| \leqslant |U(M')|</tex>, где <tex>U(M') = \{v \mid \:v \in V(G) \setminus M, \: vu \in E(G), \: u \in M'\}</tex>. |
}} | }} | ||
{{Теорема| | {{Теорема| | ||
statement= | statement= | ||
| − | + | Для произвольного графа <tex>G</tex> следующие утверждения эквивалентны: | |
| − | (1) <tex>G</tex> имеет рёберное ядро. <br> | + | (1) <tex>G</tex> имеет не пустое рёберное ядро. <br> |
(2) <tex>G</tex> имеет внешнее наименьшее вершинное покрытие. | (2) <tex>G</tex> имеет внешнее наименьшее вершинное покрытие. | ||
(3) каждое наименьшее вершинное покрытие для <tex>G</tex> является внешним. | (3) каждое наименьшее вершинное покрытие для <tex>G</tex> является внешним. | ||
| + | |proof= | ||
| + | Обозначим минимальное вершинное покрытие <tex>G</tex> как <tex>M</tex>. Пусть <tex>U = V(G) \setminus M</tex>. <br> | ||
| + | Докажем <tex>(1) \Rightarrow (3)</tex>. Предположим, что в <tex>G</tex> существует наименьшее вершинное покрытие <tex>M</tex>, которое не является внешним. | ||
| + | Это значит что <tex>\exists M' : \: M' = \{u_1, \dots, u_r \}, </tex> где <tex>r \leqslant \alpha_0(G)</tex>, | ||
| + | такое что <tex>|M'| > |U(M')|.</tex> Пусть <tex>U(M') = \{u_1, \dots, u_t\}, \: t < r</tex>. Так же, пусть <tex>X</tex> {{---}} максимальное независимое множество ребер в <tex>G</tex>. Поскольку никакие две вершины <tex>U</tex> не смежны, каждое ребро из <tex>X</tex> соединено, по крайней мере, с одной вершиной из <tex>M</tex>. Если какое-нибудь ребро из <tex>X</tex> соединено более чем с одной ввершиной из <tex>M</tex>, то <tex>|X| < \alpha_0(G)</tex> и <tex>C_1(G) = \varnothing </tex>. Так что будем считать, что каждое ребро из <tex>X</tex> смежно ровно с одной вершиной из <tex>M</tex>. Из этого сдедует, что <tex>|X| \leqslant t - r + \alpha_0(g) < \alpha_0(G)</tex>. И снова <tex>C_1(G) = \varnothing</tex>.<br> | ||
| + | Следствие <tex>(3) \Rightarrow (2)</tex> {{---}} очевидно. <br> | ||
| + | Докажем <tex>(2) \Rightarrow (1)</tex>. | ||
| + | Пусть <tex>M = \{v_1, \dots, v_s\}</tex> {{---}} наименьшее внешнее вершинное покрытие. Пусть <tex>Y_i = \{u \mid u \in U, uv_i \in E(G) \}</tex>. Тогда для любого <tex>k: \:\: 1 \leqslant k \leqslant s</tex>, объединение любых <tex>k</tex> различных множеств <tex>Y_i</tex> содержит, по меньшей мере <tex>k</tex> вершин. | ||
| + | Следовательно, по [[Теорема Холла|теореме о свадьбах (Холла)]], существует множество <tex>s</tex> различных вершин <tex>\{y_1, \dots, y_s\}, \: y_j \in Y_j</tex>. Следовательно существует набор независимых ребер <tex>y_1v_1, \dots, y_sv_s</tex>. А значит <tex>C_1(G)</tex> не может быть пустым. | ||
}} | }} | ||
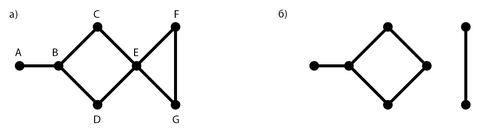
[[Файл:EdgeCore.png|thumb|500px|рис. 1. a) граф <tex>H</tex>, б) реберное ядро графа <tex>H</tex> ]] | [[Файл:EdgeCore.png|thumb|500px|рис. 1. a) граф <tex>H</tex>, б) реберное ядро графа <tex>H</tex> ]] | ||
| − | В качестве примера рассмотрим граф H изображенный на рис. 1 а). Этот граф имеет два наименьших вершинных покрытия: <tex>M_1 = \{B, E, F\}</tex> и <tex>M_2 = \{B, E, G\}</tex>. | + | В качестве примера рассмотрим граф <tex>H</tex> изображенный на рис. 1 а). Этот граф имеет два наименьших вершинных покрытия: <tex>M_1 = \{B, E, F\}</tex> и <tex>M_2 = \{B, E, G\}</tex>. |
Пусть <tex>M_1' = M_1</tex> то <tex>U(M_1') = \{A, C, D, G\}</tex>. Пусть <tex>M_1'' = \{E, F\}</tex>. Тогда <tex>U(M_1'') =\{C, D, G\}</tex>. | Пусть <tex>M_1' = M_1</tex> то <tex>U(M_1') = \{A, C, D, G\}</tex>. Пусть <tex>M_1'' = \{E, F\}</tex>. Тогда <tex>U(M_1'') =\{C, D, G\}</tex>. | ||
Отсюда <tex>|M_1'| \leqslant |U(M_1')|</tex> и <tex>|M_1''| \leqslant |U(M_1'')|</tex>. И это верно для любого подмножества <tex>M_1</tex>. Значит, <tex>M_1</tex> {{---}} внешнее покрытие. Значит и <tex>M_2</tex> {{---}} внешнее покрытие. | Отсюда <tex>|M_1'| \leqslant |U(M_1')|</tex> и <tex>|M_1''| \leqslant |U(M_1'')|</tex>. И это верно для любого подмножества <tex>M_1</tex>. Значит, <tex>M_1</tex> {{---}} внешнее покрытие. Значит и <tex>M_2</tex> {{---}} внешнее покрытие. | ||
| Строка 30: | Строка 45: | ||
==Реберное ядро в двудольном графе== | ==Реберное ядро в двудольном графе== | ||
| − | Здесь и далее будем рассматривать двудольный граф <tex>G</tex>, в котором обозначим <tex>S</tex> - множество вершин левой доли, <tex>T</tex> - множество вершин правой доли. | + | Здесь и далее будем рассматривать [[Двудольные графы|двудольный граф]] <tex>G</tex>, в котором обозначим <tex>S</tex> {{---}} множество вершин левой доли, <tex>T</tex> {{---}} множество вершин правой доли. |
{{Определение | | {{Определение | | ||
| − | definition= <tex>G</tex> {{---}} '''полунесводимый граф''', если <tex>G</tex> имеет ровно одно вершинное покрытие <tex>M</tex>, такое что или <tex>M \cap S</tex> или <tex>M \cap T</tex> {{---}} пусто | + | definition= <tex>G</tex> {{---}} '''полунесводимый граф''' (англ. ''semi-irreducible graph''), если <tex>G</tex> имеет ровно одно вершинное покрытие <tex>M</tex>, такое что или <tex>M \cap S</tex> или <tex>M \cap T</tex> {{---}} пусто |
}} | }} | ||
{{Определение| | {{Определение| | ||
definition= | definition= | ||
| − | <tex>G</tex> {{---}} '''несводимый''' граф, если он имеет ровно два наименьших вершинных покрытия <tex>M_1</tex> и <tex>M_2</tex>, таких что либо <tex>M_1 \cap S \cup M_2 \cap T = \varnothing </tex>, либо <tex>M_2 \cap S \cup M_1 \cap T = \varnothing</tex> | + | <tex>G</tex> {{---}} '''несводимый''' граф (англ. ''irreducible graph''), если он имеет ровно два наименьших вершинных покрытия <tex>M_1</tex> и <tex>M_2</tex>, таких что либо <tex>M_1 \cap S \cup M_2 \cap T = \varnothing </tex>, либо <tex>M_2 \cap S \cup M_1 \cap T = \varnothing</tex> |
}} | }} | ||
{{Определение| | {{Определение| | ||
definition= | definition= | ||
| − | <tex>G</tex> {{---}} '''сводимый граф''' если он не является ни полунесводимым, ни | + | <tex>G</tex> {{---}} '''сводимый граф''' (англ. ''reducible graph'') если он не является ни полунесводимым, ни несводимым. |
| + | }} | ||
| + | |||
| + | {{Теорема| | ||
| + | id=th2| | ||
| + | statement= | ||
| + | Если оба конца ребра <tex>w \in E(G)</tex> покрыто некоторым минимальным вершинным покрытием, то <tex>w \notin C_1(G)</tex>. | ||
| + | |proof= | ||
| + | Сошлемся на теорему 3 (Theorem 3)<ref>A. L. Dulmage and N. S. Mendelsohn, 1958, pp. 519.</ref> аналогичного результата для двудольных графов. То же самое доказательство можно перенести на произвольный граф. | ||
| + | }} | ||
| + | {{ Утверждение | ||
| + | |about=Следствие 1 | ||
| + | |statement=Eсли <tex>G</tex> имеет минимальное вершинное покрытие, которое не является независимым, то <tex>G \neq C_1(G)</tex>.<br> | ||
| + | }} | ||
| + | |||
| + | {{ Утверждение | ||
| + | |about=Следствие 2 | ||
| + | |id=proposal2 | ||
| + | |statement=Если <tex>G</tex> {{---}} сводимый связный двудольный граф, то <tex>G \neq C_1(G)</tex>. | ||
}} | }} | ||
| + | |||
| + | |||
{{Теорема| | {{Теорема| | ||
| + | id=th3| | ||
statement= | statement= | ||
| − | <tex>G</tex> и его реберное ядро <tex>C_1(G)</tex> совпадают тогда и только тогда, когда <tex>G</tex> является двудольным и не является сводимым. | + | Если <tex>G</tex> имеет непустое реберное ядро, то <tex>C_1(G) \supset G</tex>, <tex>C_1(C_1(G)) = C_1(G)</tex>, а компоненты <tex>C_1(G)</tex> являются несводимыми или полунесводимыми двудольными подграфами <tex>G</tex> |
| + | }} | ||
| + | |||
| + | {{Теорема | ||
| + | |id=th4 | ||
| + | |statement= | ||
| + | <tex>G</tex> и его реберное ядро <tex>C_1(G)</tex> совпадают тогда и только тогда, когда <tex>G</tex> является двудольным и не является сводимым. | ||
}} | }} | ||
| + | |||
| + | === Примеры === | ||
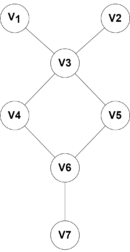
| + | [[File:Bipartite_graph_1.png|thumb|130px|Двудольный граф <tex>G_1</tex>]] | ||
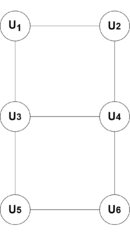
| + | [[File:Bipartite_graph_2.png|thumb|130px|Двудольный граф <tex>G_2</tex>]] | ||
| + | |||
| + | Рассмотрим двудольные графы <tex>G_1</tex> и <tex>G_2</tex>, изображенные на рисунках 1 и 2. В графе <tex>G_1</tex> пусть <tex>S_1 = \{v_3, v_6\}</tex> и <tex>T_1 = \{v_1, v_2, v_4, v_5, v_7 \}</tex>. Этот граф имеет единственное наименьшее вершинное покрытие <tex>M_1 = \{v_3, v_6\}</tex> и, поскольку <tex>M_1 \cap T_1 = \varnothing</tex>, он полунесводимый; следовательно, он совпадает со своим рёберным ядром. В графе <tex>G_2</tex> пусть <tex>S_2 = \{u_1, u_4, u_5\}</tex> и <tex>T_2 = \{u_2, u_3, u_6\}</tex>. В нём два наименьших вершинных покрытия, именно <tex>M_2 = \{u_1,u_4, u_5\}</tex> и <tex>N_2 = \{u_2, u_3, u_6\}</tex>. Так как <tex>M_2 \cap T_2 = \varnothing</tex> и <tex>N_2 \cap S_2 = \varnothing</tex>, то <tex>G_2</tex> {{---}} несводимый граф и, значит, совпадает со своим рёберным ядром. | ||
| + | <br> | ||
| + | |||
| + | == См. также == | ||
| + | * [[NP-полнота задачи о независимом множестве]] | ||
| + | * [[Теория Рамсея]] | ||
| + | * [[Связь максимального паросочетания и минимального вершинного покрытия в двудольных графах]] | ||
| + | |||
| + | ==Примечания== | ||
| + | <references /> | ||
| + | |||
| + | == Источники информации == | ||
| + | |||
| + | * [https://math.dartmouth.edu/archive/m38s12/public_html/sources/Hall1935.pdf P. Hall, On representatives of subsets, Journal of the London Mathematical Society 10 (1935) pp. 26-30.] | ||
| + | |||
| + | * [https://cms.math.ca/openaccess/cjm/v10/cjm1958v10.0517-0534.pdf A. L. Dulmage and N. S. Mendelsohn: Coverings of bipartite graphs, Canad J. Math., (1958), 517-534.] | ||
| + | |||
| + | [[Категория: Алгоритмы и структуры данных]] | ||
| + | [[Категория: Основные определения теории графов]] | ||
Текущая версия на 19:07, 4 сентября 2022
| Определение: |
| Рёберное ядро (англ. core) графа — это подграф графа , порожденный объединением таких независимых множеств , что , где — число вершинного покрытия. |
| Определение: |
| Множество ребер (вершин) называется независимым (англ. independent), если никакие его два элемента не смежны. |
| Определение: |
| Вершинным покрытием (англ. vertex cover) графа называется такое множество его вершин, что у любого ребра в хотя бы одна из вершин лежит в . |
| Определение: |
| Числом вершинного покрытия (англ. point-covering number) называется число вершин в наименьшем вершинном покрытии графа . |
Содержание
Критерий существования реберного ядра
| Определение: |
| Наименьшее вершинное покрытие графа с множеством вершин называется внешним (англ. external vertex cover), если для любого подмножества выполняется неравенство , где . |
| Теорема: |
Для произвольного графа следующие утверждения эквивалентны:
(1) имеет не пустое рёберное ядро. |
| Доказательство: |
|
Обозначим минимальное вершинное покрытие как . Пусть . |
В качестве примера рассмотрим граф изображенный на рис. 1 а). Этот граф имеет два наименьших вершинных покрытия: и .
Пусть то . Пусть . Тогда .
Отсюда и . И это верно для любого подмножества . Значит, — внешнее покрытие. Значит и — внешнее покрытие.
Реберное ядро в двудольном графе
Здесь и далее будем рассматривать двудольный граф , в котором обозначим — множество вершин левой доли, — множество вершин правой доли.
| Определение: |
| — полунесводимый граф (англ. semi-irreducible graph), если имеет ровно одно вершинное покрытие , такое что или или — пусто |
| Определение: |
| — несводимый граф (англ. irreducible graph), если он имеет ровно два наименьших вершинных покрытия и , таких что либо , либо |
| Определение: |
| — сводимый граф (англ. reducible graph) если он не является ни полунесводимым, ни несводимым. |
| Теорема: |
Если оба конца ребра покрыто некоторым минимальным вершинным покрытием, то . |
| Доказательство: |
| Сошлемся на теорему 3 (Theorem 3)[1] аналогичного результата для двудольных графов. То же самое доказательство можно перенести на произвольный граф. |
| Утверждение (Следствие 1): |
Eсли имеет минимальное вершинное покрытие, которое не является независимым, то . |
| Утверждение (Следствие 2): |
Если — сводимый связный двудольный граф, то . |
| Теорема: |
Если имеет непустое реберное ядро, то , , а компоненты являются несводимыми или полунесводимыми двудольными подграфами |
| Теорема: |
и его реберное ядро совпадают тогда и только тогда, когда является двудольным и не является сводимым. |
Примеры
Рассмотрим двудольные графы и , изображенные на рисунках 1 и 2. В графе пусть и . Этот граф имеет единственное наименьшее вершинное покрытие и, поскольку , он полунесводимый; следовательно, он совпадает со своим рёберным ядром. В графе пусть и . В нём два наименьших вершинных покрытия, именно и . Так как и , то — несводимый граф и, значит, совпадает со своим рёберным ядром.
См. также
- NP-полнота задачи о независимом множестве
- Теория Рамсея
- Связь максимального паросочетания и минимального вершинного покрытия в двудольных графах
Примечания
- ↑ A. L. Dulmage and N. S. Mendelsohn, 1958, pp. 519.