Теорема Бермана — Форчуна — различия между версиями
AndrewD (обсуждение | вклад) |
м (rollbackEdits.php mass rollback) |
||
| (не показаны 23 промежуточные версии 7 участников) | |||
| Строка 1: | Строка 1: | ||
{{Лемма | {{Лемма | ||
|about=1 | |about=1 | ||
| − | |statement=<tex>L \in | + | |statement=Язык <tex>L</tex> является <tex>\mathrm{coNP}</tex>-полным тогда и только тогда, когда <tex>\overline L</tex> является <tex>\mathrm{NP}</tex>-полным (то есть <tex>L \in \mathrm{coNP\mbox{-}C} \Leftrightarrow L \in \mathrm{co\mbox{-}NPC}</tex>). |
| − | |proof=Пусть <tex>L \ | + | |proof=Пусть <tex>L</tex> {{---}} <tex>\mathrm{coNP}</tex>-полный. Тогда <tex>L \in \mathrm{coNP}</tex> и <tex>\overline L \in \mathrm{NP}</tex>. |
| − | Рассмотрим произвольный язык <tex>L_1 \in NP</tex>. Тогда <tex>\overline {L_1} \in coNP</tex>. Так как <tex>L \ | + | Рассмотрим произвольный язык <tex>L_1 \in \mathrm{NP}</tex>. Тогда <tex>\overline {L_1} \in \mathrm{coNP}</tex>. Так как <tex>L</tex> {{---}} <tex>\mathrm{coNP}</tex>-полный, то <tex>\overline {L_1} \le L</tex>, следовательно <tex>L_1 \le \overline L</tex> (по [[Сведение относительно класса функций. Сведение по Карпу. Трудные и полные задачи#lemma|лемме]]). |
| − | Получили, что <tex>\overline L \in NP</tex> и <tex>\forall L_1 \in NP \ | + | Получили, что <tex>\overline L \in \mathrm{NP}</tex> и <tex>\forall L_1 \in \mathrm{NP} \Rightarrow L_1 \le \overline L</tex>. Значит <tex>\overline L \in \mathrm{NPC}</tex>. |
В обратную сторону доказательство аналогично. | В обратную сторону доказательство аналогично. | ||
}} | }} | ||
| Строка 12: | Строка 12: | ||
{{Определение | {{Определение | ||
|definition= | |definition= | ||
| − | <tex>TAUT = \{\phi</tex> {{---}} булева формула <tex>| \forall x \, \phi(x)=1\}</tex>. | + | <tex>\mathrm{TAUT} = \{\phi</tex> {{---}} булева формула <tex>\bigm{|} \forall x = (x_1, x_2, \ldots , x_m) \, \phi(x)=1\}</tex>. |
}} | }} | ||
{{Лемма | {{Лемма | ||
|about=2 | |about=2 | ||
| − | |statement=<tex>TAUT \in coNPC</tex> | + | |statement=<tex>\mathrm{TAUT} \in \mathrm{coNPC}</tex>. |
| − | |proof=<tex>\overline {TAUT} = \{\phi | \exists x : \phi(x) \ne 1\} = \{\phi | \overline {\phi} \in SAT\}</tex>, то есть <tex>\overline {TAUT} \in NPC</tex>. Тогда по лемме (1) <tex>TAUT \in coNPC</tex>. | + | |proof=<tex>\overline {\mathrm{TAUT}} = \{\phi \bigm{|} \exists x : \phi(x) \ne 1\} = \{\phi \bigm{|} \overline {\phi} \in \mathrm{SAT}\}</tex>, то есть <tex>\mathrm{SAT} \le \overline {\mathrm{TAUT}} \, (f(\phi) = \overline {\phi})</tex>. Кроме того, <tex>\overline {\mathrm{TAUT}} \in \mathrm{NP}</tex> <tex>(</tex>в качестве сертификата используется <tex>x</tex>, на котором <tex>\phi(x) \ne 1)</tex>. Значит <tex>\overline{\mathrm{TAUT}} \in \mathrm{NPC}</tex>. Тогда по лемме (1) <tex>\mathrm{TAUT} \in \mathrm{coNPC}</tex>. |
}} | }} | ||
{{Определение | {{Определение | ||
|definition= | |definition= | ||
| − | <tex>SPARSE = \{L | \exists</tex> полином <tex>p: \forall n \, |L \cap \Sigma^n| \le p(n)\}</tex>. | + | <tex>\mathrm{SPARSE} = \{L \bigm{|} \exists</tex> полином <tex>p: \forall n \, |L \cap \Sigma^n| \le p(n)\}</tex>. |
}} | }} | ||
{{Теорема | {{Теорема | ||
| − | + | |statement=<tex>\mathrm{coNPC} \cap \mathrm{SPARSE} \ne \varnothing \Rightarrow \mathrm{P} = \mathrm{NP}</tex>. | |
| − | + | |author=Берман, Форчун | |
| − | |statement=<tex>coNPC \cap SPARSE | + | |proof=Пусть существует <tex>S \in \mathrm{coNPC} \cap \mathrm{SPARSE}</tex>. Разрешим <tex>\mathrm{TAUT}</tex> за полином. |
| − | |proof=Пусть существует <tex>S \in coNPC \cap SPARSE</tex>. Разрешим <tex>TAUT</tex> за полином. | ||
| − | Для начала напишем программу, разрешающую <tex>TAUT</tex>: | + | Для начала напишем программу, разрешающую <tex>\mathrm{TAUT}</tex>: |
| − | <tex>check(\phi, i)</tex> | + | <tex>check(\phi, i)</tex>: |
| − | |||
| − | |||
'''if''' <tex>\phi=0</tex> | '''if''' <tex>\phi=0</tex> | ||
'''return''' 0 | '''return''' 0 | ||
'''if''' <tex>\phi=1</tex> | '''if''' <tex>\phi=1</tex> | ||
'''return''' 1 | '''return''' 1 | ||
| − | <tex>memo[\phi] \leftarrow check(\phi|_{x_i=0}, i+1)\ | + | '''if''' <tex>memo[\phi] \ne -1</tex> |
| + | '''return''' <tex>memo[\phi]</tex> | ||
| + | <tex>memo[\phi] \leftarrow check(\phi|_{x_i=0}, i+1) \wedge check(\phi|_{x_i=1}, i+1)</tex> | ||
'''return''' <tex>memo[\phi]</tex> | '''return''' <tex>memo[\phi]</tex> | ||
Ответом будет <tex>check(\phi, 1)</tex>. | Ответом будет <tex>check(\phi, 1)</tex>. | ||
| − | Так как <tex>TAUT \in coNPC</tex> и <tex>S \in coNPC</tex>, то <tex>TAUT \ | + | Так как <tex>\mathrm{TAUT} \in \mathrm{coNPC}</tex> и <tex>S \in \mathrm{coNPC}</tex>, то <tex>\mathrm{TAUT} \le S</tex>, то есть <tex>\exists f \in \mathrm{\widetilde{P}} : \phi \in \mathrm{TAUT} \Leftrightarrow f(\phi) \in S</tex>. Поэтому, если в предыдущей программе заменить все обращения к <tex>memo[\phi]</tex>, на <tex>memo[f(\phi)]</tex>, то полученная программа по-прежнему будет разрешать <tex>\mathrm{TAUT}</tex>. |
| − | Оценим необходимый размер <tex>memo</tex>. Можно считать, что <tex>T(f | + | Оценим необходимый размер <tex>memo</tex>. Можно считать, что <tex>\mathrm{T}(f, \phi) \le q(n)</tex>, где <tex>n = |\phi|</tex>, а <tex>q</tex> {{---}} монотонно возрастающий полином. Тогда <tex>|f(\phi)| \le q(n)</tex>. Так как <tex>S \in \mathrm{SPARSE}</tex>, то <tex>|S \cap \Sigma^k| \le p(k)</tex>, где <tex>p</tex> {{---}} полином. Можно считать, что <tex>p</tex> монотонно возрастает. Тогда размер <tex>memo</tex> (число слов длины не более <tex>q(n)</tex> в языке) можно оценить сверху: <tex>memo.size() \le \sum\limits_{i=0}^{q(n)}p(i) \le (1+q(n)) \cdot p(q(n)) \le r(n)</tex>, где <tex>r(n)</tex> {{---}} полином. |
| − | <tex>check(\phi, i)</tex> | + | <tex>check(\phi, i)</tex>: |
| − | |||
| − | |||
'''if''' <tex>\phi=0</tex> | '''if''' <tex>\phi=0</tex> | ||
| − | ''' | + | '''exit''' 0 |
'''if''' <tex>\phi=1</tex> | '''if''' <tex>\phi=1</tex> | ||
'''return''' 1 | '''return''' 1 | ||
| − | <tex>memo[f(\phi)] \leftarrow check(\phi|_{x_i=0}, i+1)\ | + | '''if''' <tex>memo[f(\phi)] \ne -1</tex> //(1) |
| + | '''return''' <tex>memo[f(\phi)]</tex> | ||
| + | <tex>memo[f(\phi)] \leftarrow check(\phi|_{x_i=0}, i+1) \wedge check(\phi|_{x_i=1}, i+1)</tex> //(2) | ||
'''if''' <tex>memo.size() > r(n)</tex> | '''if''' <tex>memo.size() > r(n)</tex> | ||
'''exit''' <tex>0</tex> | '''exit''' <tex>0</tex> | ||
'''return''' <tex>memo[f(\phi)]</tex> | '''return''' <tex>memo[f(\phi)]</tex> | ||
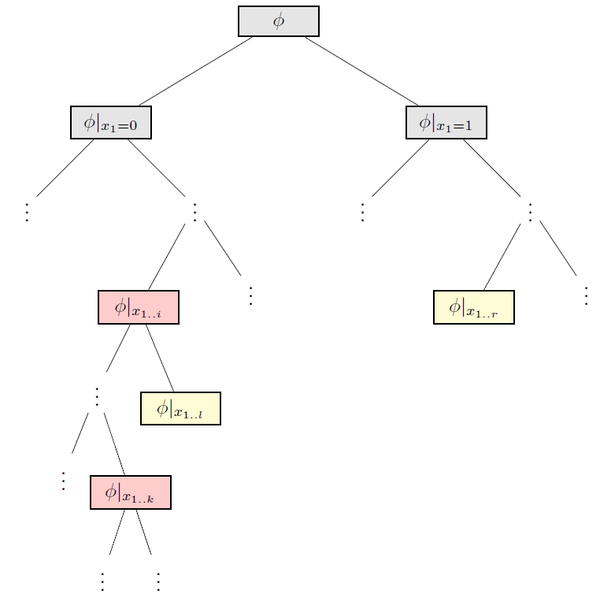
| + | [[Файл:Berman-Fortune.png|thumb|upright=2.0|Двоичное дерево, получающееся в результате рекурсивных вызовов модифицированной программы. Красным и желтым помечены узлы, в которых происходит обращение к элементу ''memo[j]''. В красных узлах условие ''(1)'' ложно, в желтых {{---}} истинно.]] | ||
Рассмотрим двоичное дерево, получающееся в результате рекурсивных вызовов данной программы. | Рассмотрим двоичное дерево, получающееся в результате рекурсивных вызовов данной программы. | ||
| − | Рассмотрим произвольный элемент <tex>memo[ | + | Рассмотрим произвольный элемент <tex>memo[j]</tex>. Найдем, сколько раз условие <tex>(1)</tex> в ходе выполнения программы является ложным при обращении к элементу <tex>memo[j]</tex>. Найдем в дереве такой узел, в котором есть обращение к <tex>memo[j]</tex>, а в его поддереве обращений к этому элементу нет, причем <tex>memo[j] = -1</tex>. До этого момента количество обращений к <tex>memo[j]</tex> не превышает глубины найденного узла, что не превосходит высоты дерева, что не превосходит некоторого полинома <tex>p'(n)</tex>. После этого момента условие <tex>(1)</tex> будет принимать истинное значение при обращении к <tex>memo[j]</tex>. Значит, в ходе выполнения программы условие <tex>(1)</tex> является ложным при обращении к <tex>memo[j]</tex> не более <tex>p'(n)</tex> раз. |
| + | |||
| + | Так как всего в <tex>memo</tex> не более <tex>r(n)</tex> элементов, то суммарно за все время выполнения программы условие <tex>(1)</tex> принимает ложное значение не более <tex>p''(n) = r(n) \cdot p'(n)</tex> раз, то есть <tex>p''</tex> {{---}} полином. Отсюда следует, что присваивание <tex>(2)</tex> выполняется не более <tex>p''(n)</tex> раз, а значит в дереве не более <tex>p''(n)</tex> внутренних вершин. Значит всего в дереве не более <tex>2 \cdot p''(n) + 1</tex> вершин, то есть данная программа работает за полиномиальное время. | ||
| − | Итого, данная программа разрешает <tex>TAUT</tex> за полиномиальное время. А так как <tex>TAUT \in coNPC</tex>, то <tex>P=coNP</tex>, то есть <tex>coP=coNP</tex>, откуда <tex>P=NP</tex>. | + | Итого, данная программа разрешает <tex>\mathrm{TAUT}</tex> за полиномиальное время. А так как <tex>\mathrm{TAUT} \in \mathrm{coNPC}</tex>, то <tex>\mathrm{P}=\mathrm{coNP}</tex>, то есть <tex>\mathrm{coP}=\mathrm{coNP}</tex>, откуда <tex>\mathrm{P}=\mathrm{NP}</tex>. |
}} | }} | ||
| + | |||
| + | == См. также == | ||
| + | *[[Класс P]] | ||
| + | *[[Классы NP и Σ₁]] | ||
| + | |||
| + | [[Категория: Теория сложности]] | ||
Текущая версия на 19:10, 4 сентября 2022
| Лемма (1): |
Язык является -полным тогда и только тогда, когда является -полным (то есть ). |
| Доказательство: |
|
Пусть — -полный. Тогда и . Рассмотрим произвольный язык . Тогда . Так как — -полный, то , следовательно (по лемме). Получили, что и . Значит . В обратную сторону доказательство аналогично. |
| Определение: |
| — булева формула . |
| Лемма (2): |
. |
| Доказательство: |
| , то есть . Кроме того, в качестве сертификата используется , на котором . Значит . Тогда по лемме (1) . |
| Определение: |
| полином . |
| Теорема (Берман, Форчун): |
. |
| Доказательство: |
|
Пусть существует . Разрешим за полином. Для начала напишем программу, разрешающую : : if return 0 if return 1 if return return Ответом будет . Так как и , то , то есть . Поэтому, если в предыдущей программе заменить все обращения к , на , то полученная программа по-прежнему будет разрешать . Оценим необходимый размер . Можно считать, что , где , а — монотонно возрастающий полином. Тогда . Так как , то , где — полином. Можно считать, что монотонно возрастает. Тогда размер (число слов длины не более в языке) можно оценить сверху: , где — полином. : if exit 0 if return 1 if //(1) return //(2) if exit return Рассмотрим двоичное дерево, получающееся в результате рекурсивных вызовов данной программы. Рассмотрим произвольный элемент . Найдем, сколько раз условие в ходе выполнения программы является ложным при обращении к элементу . Найдем в дереве такой узел, в котором есть обращение к , а в его поддереве обращений к этому элементу нет, причем . До этого момента количество обращений к не превышает глубины найденного узла, что не превосходит высоты дерева, что не превосходит некоторого полинома . После этого момента условие будет принимать истинное значение при обращении к . Значит, в ходе выполнения программы условие является ложным при обращении к не более раз. Так как всего в не более элементов, то суммарно за все время выполнения программы условие принимает ложное значение не более раз, то есть — полином. Отсюда следует, что присваивание выполняется не более раз, а значит в дереве не более внутренних вершин. Значит всего в дереве не более вершин, то есть данная программа работает за полиномиальное время. Итого, данная программа разрешает за полиномиальное время. А так как , то , то есть , откуда . |