|
|
| Строка 1: |
Строка 1: |
| − | {| class="wikitable" align="center" style="color: red; background-color: black; font-size: 56px; width: 800px;"
| |
| − | |+
| |
| − | |-align="center"
| |
| − | |'''НЕТ ВОЙНЕ'''
| |
| − | |-style="font-size: 16px;"
| |
| − | |
| |
| − | 24 февраля 2022 года российское руководство во главе с Владимиром Путиным развязало агрессивную войну против Украины. В глазах всего мира это военное преступление совершено от лица всей страны, всех россиян.
| |
| − |
| |
| − | Будучи гражданами Российской Федерации, мы против своей воли оказались ответственными за нарушение международного права, военное вторжение и массовую гибель людей. Чудовищность совершенного преступления не оставляет возможности промолчать или ограничиться пассивным несогласием.
| |
| − |
| |
| − | Мы убеждены в абсолютной ценности человеческой жизни, в незыблемости прав и свобод личности. Режим Путина — угроза этим ценностям. Наша задача — обьединить все силы для сопротивления ей.
| |
| − |
| |
| − | Эту войну начали не россияне, а обезумевший диктатор. И наш гражданский долг — сделать всё, чтобы её остановить.
| |
| − |
| |
| − | ''Антивоенный комитет России''
| |
| − | |-style="font-size: 16px;"
| |
| − | |Распространяйте правду о текущих событиях, оберегайте от пропаганды своих друзей и близких. Изменение общественного восприятия войны - ключ к её завершению.
| |
| − | |-style="font-size: 16px;"
| |
| − | |[https://meduza.io/ meduza.io], [https://www.youtube.com/c/popularpolitics/videos Популярная политика], [https://novayagazeta.ru/ Новая газета], [https://zona.media/ zona.media], [https://www.youtube.com/c/MackNack/videos Майкл Наки].
| |
| − | |}
| |
| − |
| |
| | Дан неориентированный [[Основные определения теории графов#Граф| граф]] <tex> G </tex>. Найти все [[Мост, эквивалентные определения | мосты]] в <tex> G </tex> за время <tex> O(|V| + |E|)</tex> | | Дан неориентированный [[Основные определения теории графов#Граф| граф]] <tex> G </tex>. Найти все [[Мост, эквивалентные определения | мосты]] в <tex> G </tex> за время <tex> O(|V| + |E|)</tex> |
| | | | |
Текущая версия на 19:12, 4 сентября 2022
Дан неориентированный граф [math] G [/math]. Найти все мосты в [math] G [/math] за время [math] O(|V| + |E|)[/math]
Алгоритм
| Теорема: |
Пусть [math] T [/math] — дерево обхода в глубину графа [math] G[/math]. Ребро [math] (u, v) [/math] является мостом тогда и только тогда, когда [math] (u, v) \in T[/math] и из вершины [math] v[/math] и любого ее потомка нет обратного ребра в вершину [math] u[/math] или предка [math] u [/math] |
| Доказательство: |
| [math]\triangleright[/math] |
|
[math] \Leftarrow[/math]
Удалим [math] (u, v)[/math] из [math] G[/math]. Докажем, что мы не сможем достичь ни одного из предков [math] v [/math] (в частности [math] u [/math]). Докажем этот факт от противного.
Пусть это не так, и [math] w[/math] — предпоследняя вершина на пути от [math] v[/math] до ее предка [math]x [/math]. Очевидно, [math] (w, x)[/math] не ребро дерева (в силу единственности пути в дереве). Если [math] (w, x)[/math] — обратное ребро, то это противоречит условию теоремы, так как [math] x[/math] — предок [math] u[/math]. Следовательно мы не достигнем предков [math]v[/math], а значит количество компонент связности увеличилось, поэтому ребро [math](u, v)[/math] является мостом.
[math] \Rightarrow[/math]
Пусть существует удовлетворяющее условию обратное ребро [math](x, w)[/math]. Тогда [math](u, v)[/math] лежит на цикле [math]x \rightsquigarrow v \rightarrow u \rightsquigarrow w \rightarrow x[/math] и не может быть мостом. |
| [math]\triangleleft[/math] |
Функция [math]ret(v)[/math]
Определим функцию [math]ret(v)[/math], где [math]v \in V[/math], как минимум из следущих величин
- [math]enter(v)[/math] время входа в вершину [math]v [/math]
- [math]enter(x)[/math], где [math]x[/math] — потомок [math]v[/math]
- [math]enter(w)[/math], где [math](w, x)[/math] — обратное ребро, а [math]w[/math] — потомок [math]v[/math] (в нестрогом смысле)
Лемма
| Лемма: |
Ребро [math](u, v)[/math] является мостом тогда и только тогда, когда [math](u, v)[/math] принадлежит дереву обхода в глубину и [math]ret(v) \gt enter(u)[/math] |
| Доказательство: |
| [math]\triangleright[/math] |
|
Рассмотрим вершину [math]v[/math] или её потомка. Из нее есть обратное ребро в предка [math]v[/math] тогда и только тогда, когда найдется такой сын [math]t[/math], что [math]ret[t] \le enter[v][/math]. Если [math]ret[t] = enter[v][/math], то найдется обратное ребро, приходящее точно в [math]v[/math]. Если же [math]ret[t] \lt enter[v][/math], то это означает наличие обратного ребра в какого-либо предка вершины [math]v[/math].
Таким образом, если для текущего ребра [math](v, t)[/math] (принадлежащего дереву поиска) выполняется [math]ret[t] \gt enter[v][/math], то это ребро является мостом; в противном случае оно мостом не является. |
| [math]\triangleleft[/math] |
| Утверждение: |
[math]ret(v)[/math] = [math]\min([/math] [math]enter(v) [/math], [math]enter(p)[/math], [math]ret(u)[/math]
[math]) [/math], где
[math](v, p)[/math] — обратное ребро,
[math](v, u)[/math] — ребро дерева |
| [math]\triangleright[/math] |
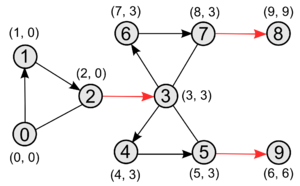 В скобах у вершины [math]u[/math] указаны [math]enter[u][/math] и [math]ret[u][/math]. Мостами будут красные ребра - [math]enter(v) [/math]
По определению функции [math]ret[/math]
- [math]enter(p)[/math], [math](v, p)[/math] — обратное ребро
[math]p[/math] достижима из [math]v[/math] по одному обратному ребру, значит величина [math]ret(v)[/math] не больше [math]enter(p)[/math]
- [math]ret(u)[/math], [math]u[/math] — потомок [math]v[/math]
Так как вершина [math]u[/math] — потомок [math]v[/math], то обратное ребро из ее поддерева является обратным ребром из поддерева [math]v[/math]
|
| [math]\triangleleft[/math] |
Псевдокод
function dfs(v):
time = time + 1
enter[v] = time
ret[v] = time
for всех u смежных с v
if (v, u) — обратное ребро
ret[v] = min(ret[v], enter[u])
if вершина u — белая
dfs(u)
ret[v] = min(ret[v], ret[u])
if ret[u] > enter[v]
ребро (v, u) — мост
См. также
Источники информации
