Переобучение — различия между версиями
Evaleria (обсуждение | вклад) м (→На примере линейной регрессии) |
м (rollbackEdits.php mass rollback) |
||
| (не показано 57 промежуточных версий 12 участников) | |||
| Строка 1: | Строка 1: | ||
| − | '''Переобучение''' (англ. overfitting) {{---}} негативное явление, возникающее, когда алгоритм обучения вырабатывает предсказания, которые слишком близко или точно соответствуют конкретному набору данных | + | '''Переобучение''' (англ. overfitting) {{---}} негативное явление, возникающее, когда алгоритм обучения вырабатывает предсказания, которые слишком близко или точно соответствуют конкретному набору данных и поэтому не подходят для применения алгоритма к дополнительным данным или будущим наблюдениям. |
| − | '''Недообучение''' (англ. underfitting) {{---}} негативное явление, | + | '''Недообучение''' (англ. underfitting) {{---}} негативное явление, при котором алгоритм обучения не обеспечивает достаточно малой величины средней ошибки на обучающей выборке. Недообучение возникает при использовании недостаточно сложных моделей. |
== Примеры == | == Примеры == | ||
| − | === На примере линейной регрессии === | + | |
| − | Представьте задачу | + | |
| + | === На примере [[Линейная регрессия | линейной регрессии]] === | ||
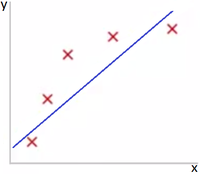
| + | Представьте задачу линейной регрессии. Красные точки представляют исходные данные. Синие линии являются графиками полиномов различной степени M, аппроксимирующих исходные данные. | ||
| + | |||
{|align="center" | {|align="center" | ||
|-valign="top" | |-valign="top" | ||
| − | |[[Файл:High_bias_reg.png|200px|thumb|Рис 1. Недообучение]] | + | |[[Файл:High_bias_reg.png|200px|thumb|Рис 1. Недообучение. M=1]] |
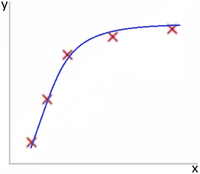
| − | |[[Файл:Normal_bias_reg.png|200px|thumb|Рис 2. | + | |[[Файл:Normal_bias_reg.png|200px|thumb|Рис 2. Норма. M=2]] |
| − | |[[Файл:High_variance_reg.png|200px|thumb|Рис 3. Переобучение]] | + | |[[Файл:High_variance_reg.png|200px|thumb|Рис 3. Переобучение. M=4]] |
|} | |} | ||
| − | |||
| − | === На примере логистической регрессии === | + | Как видно из Рис. 1, данные не поддаются линейной зависимости при небольшой степени полинома и по этой причине модель, представленная на данном рисунке, не очень хороша. |
| − | Представьте задачу классификации | + | |
| + | На Рис. 2 представлена ситуация, когда выбранная полиномиальная функция подходит для описания исходных данных. | ||
| + | |||
| + | Рис. 3 иллюстрирует случай, когда высокая степень полинома ведет к тому, что модель слишком заточена на данные обучающего датасета. | ||
| + | |||
| + | === На примере [[Логистическая регрессия | логистической регрессии]] === | ||
| + | |||
| + | |||
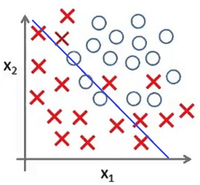
| + | Представьте задачу классификации размеченных точек. Красные точки представляют данные класса 1. Голубые круглые точки {{---}} класса 2. Синие линии являются представлением различных моделей, которыми производится классификация данных. | ||
| + | |||
{|align="center" | {|align="center" | ||
|-valign="top" | |-valign="top" | ||
|[[Файл:High_bias_cla.png|200px|thumb|Рис 4. Недообучение]] | |[[Файл:High_bias_cla.png|200px|thumb|Рис 4. Недообучение]] | ||
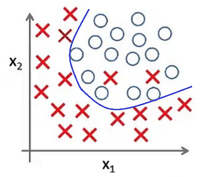
| − | |[[Файл:Normal_bias_cla.png|200px|thumb|Рис 5. | + | |[[Файл:Normal_bias_cla.png|200px|thumb|Рис 5. Подходящая модель]] |
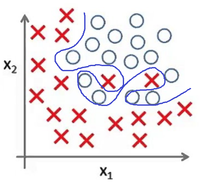
|[[Файл:High_variance_cla.png|200px|thumb|Рис 6. Переобучение]] | |[[Файл:High_variance_cla.png|200px|thumb|Рис 6. Переобучение]] | ||
|} | |} | ||
| − | + | Рис. 4 показывает результат использования слишком простой модели для представленного датасета | |
== Кривые обучения == | == Кривые обучения == | ||
| + | '''Кривая обучения''' {{---}} графическое представление того, как изменение меры обученности (по вертикальной оси) зависит от определенной единицы измерения опыта (по горизонтальной оси)<ref>[https://en.wikipedia.org/wiki/Learning_curve Wikipedia {{---}} Learning curve]</ref>. Например, в примерах ниже представлена зависимость средней ошибки от объема датасета. | ||
| + | |||
=== Кривые обучения при переобучении === | === Кривые обучения при переобучении === | ||
| − | [[Файл:High_variance_learning_curve.png|border| | + | При переобучении небольшая средняя ошибка на обучающей выборке не обеспечивает такую же малую ошибку на тестовой выборке. |
| + | |||
| + | {|align="center" | ||
| + | |-valign="top" | ||
| + | |[[Файл:High_variance_learning_curve.png|border|400px|Кривые обучения при переобучении|thumb|Рис 7. Кривые обучения при переобучении]] | ||
| + | |} | ||
| + | |||
| + | Рис. 7 демонстрирует зависимость средней ошибки для обучающей и тестовой выборок от объема датасета при переобучении. | ||
| + | |||
=== Кривые обучения при недообучении === | === Кривые обучения при недообучении === | ||
| − | [[Файл:High_bias_learning_curve.png|border| | + | При недообучении независимо от объема обучающего датасета как на обучающей выборке, так и на тестовой выборке небольшая средняя ошибка не достигается. |
| + | |||
| + | {|align="center" | ||
| + | |-valign="top" | ||
| + | |[[Файл:High_bias_learning_curve.png|border|400px|Кривые обучения при переобучении|thumb|Рис 8. Кривые обучения при недообучении]] | ||
| + | |} | ||
| + | |||
| + | Рис. 8 демонстрирует зависимость средней ошибки для обучающей и тестовой выборок от объема датасета при недообучении. | ||
== High variance и high bias == | == High variance и high bias == | ||
| − | '''Bias''' {{---}} ошибка неверных предположений в алгоритме обучения. Высокий bias может привести к недообучению. | + | '''Bias''' {{---}} ошибка неверных предположений в алгоритме обучения. Высокий '''bias''' может привести к недообучению. |
| − | '''Variance''' {{---}} | + | '''Variance''' {{---}} ошибка, вызванная большой чувствительностью к небольшим отклонениям в тренировочном наборе. Высокая дисперсия может привести к переобучению. |
{|align="center" | {|align="center" | ||
| Строка 40: | Строка 68: | ||
|} | |} | ||
| − | При использовании нейронных сетей variance увеличивается, а bias уменьшается с увеличением количества скрытых слоев. | + | При использовании нейронных сетей '''variance''' увеличивается, а '''bias''' уменьшается с увеличением количества скрытых слоев. |
| − | Для устранения high variance и high bias можно использовать смеси и ансамбли. Например, можно составить ансамбль (boosting) из нескольких моделей с высоким bias и получить модель с небольшим bias. В другом случае при bagging соединяются несколько моделей с низким bias, а результирующая модель позволяет уменьшить variance. | + | Для устранения '''high variance''' и '''high bias''' можно использовать смеси и ансамбли. Например, можно составить ансамбль ('''boosting''') из нескольких моделей с высоким '''bias''' и получить модель с небольшим '''bias'''. В другом случае при '''bagging''' соединяются несколько моделей с низким '''bias''', а результирующая модель позволяет уменьшить '''variance'''. |
| + | |||
| + | ===Дилемма bias–variance === | ||
| + | |||
| + | |||
| + | |||
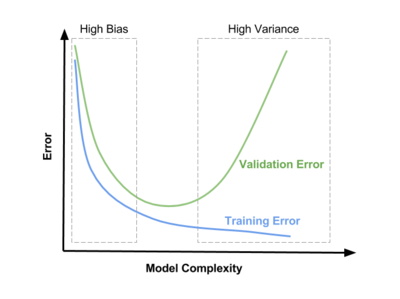
| + | '''Дилемма bias–variance''' {{---}} конфликт в попытке одновременно минимизировать '''bias''' и '''variance''', тогда как уменьшение одного из негативных эффектов, приводит к увеличению другого. Данная дилемма проиллюстрирована на Рис 10. | ||
| + | |||
| + | {|align="center" | ||
| + | |-valign="top" | ||
| + | |[[Файл:Bias-Variance-Tradeoff.png|border|400px|thumb|right|Рис 10. Дилемма bias–variance]] | ||
| + | |} | ||
| + | |||
| + | При небольшой сложности модели мы наблюдаем '''high bias'''. При усложнении модели '''bias''' уменьшается, но '''variance''' увеличится, что приводит к проблеме '''high variance'''. | ||
== Возможные решения == | == Возможные решения == | ||
=== Возможные решения при переобучении === | === Возможные решения при переобучении === | ||
| − | * Увеличение количества данных в наборе | + | * Увеличение количества данных в наборе; |
| − | * Уменьшение количества параметров модели | + | * Уменьшение количества параметров модели; |
| − | * Добавление регуляризации / увеличение коэффициента регуляризации | + | * Добавление регуляризации / увеличение коэффициента регуляризации. |
=== Возможные решения при недообучении === | === Возможные решения при недообучении === | ||
| − | * Добавление новых параметров модели | + | * Добавление новых параметров модели; |
| − | * Использование для описания модели функций с более высокой степенью | + | * Использование для описания модели функций с более высокой степенью; |
| − | * Уменьшение коэффициента регуляризации | + | * Уменьшение коэффициента регуляризации. |
== См. также == | == См. также == | ||
| − | * [ | + | * [[Модель алгоритма и ее выбор]] |
| − | * [ | + | * [[Оценка качества в задачах классификации и регрессии]]<sup>[на 28.01.19 не создан]</sup> |
| − | * [ | + | * [[Оценка качества в задаче кластеризации]] |
== Примечания == | == Примечания == | ||
| + | <references/> | ||
| + | |||
| + | == Источники информации == | ||
| + | * [https://www.coursera.org/lecture/machine-learning/the-problem-of-overfitting-ACpTQ The Problem of Overfitting on Coursera, Andrew Ng] | ||
* [http://blog.lokad.com/journal/2009/4/22/overfitting-when-accuracy-measure-goes-wrong.html Overfitting: when accuracy measure goes wrong] | * [http://blog.lokad.com/journal/2009/4/22/overfitting-when-accuracy-measure-goes-wrong.html Overfitting: when accuracy measure goes wrong] | ||
* [http://www3.cs.stonybrook.edu/~skiena/jaialai/excerpts/node16.html The Problem of Overfitting Data] | * [http://www3.cs.stonybrook.edu/~skiena/jaialai/excerpts/node16.html The Problem of Overfitting Data] | ||
* [https://elitedatascience.com/overfitting-in-machine-learning Overfitting in Machine Learning] | * [https://elitedatascience.com/overfitting-in-machine-learning Overfitting in Machine Learning] | ||
| − | + | * [https://en.wikipedia.org/wiki/Overfitting Overfitting] - статься на Википедии | |
| − | + | * [http://www.machinelearning.ru/wiki/index.php?title=Переобучение Переобучение] - вводная статься на MachineLearning.ru | |
| − | + | * [https://www.coursera.org/lecture/machine-learning/the-problem-of-overfitting-ACpTQ The Problem of Overfitting] - курс Andrew Ng | |
| − | + | * ''Hastie, T., Tibshirani, R., Friedman, J. '' [http://www-stat.stanford.edu/~tibs/ElemStatLearn The Elements of Statistical Learning, 2nd edition.] — Springer, 2009. — 533 p. | |
| − | + | * ''Vapnik V.N. '' [http://lib.mexmat.ru/books/9220 Statistical learning theory.] — N.Y.: John Wiley & Sons, Inc., 1998. | |
| − | + | * ''Воронцов, К. В. '' [http://www.machinelearning.ru/wiki/images/b/b6/Voron10doct.pdf Комбинаторная теория надёжности обучения по прецедентам]: Дис. док. физ.-мат. наук: 05-13-17. — Вычислительный центр РАН, 2010. — 271 с. | |
| − | |||
| − | |||
Текущая версия на 19:13, 4 сентября 2022
Переобучение (англ. overfitting) — негативное явление, возникающее, когда алгоритм обучения вырабатывает предсказания, которые слишком близко или точно соответствуют конкретному набору данных и поэтому не подходят для применения алгоритма к дополнительным данным или будущим наблюдениям.
Недообучение (англ. underfitting) — негативное явление, при котором алгоритм обучения не обеспечивает достаточно малой величины средней ошибки на обучающей выборке. Недообучение возникает при использовании недостаточно сложных моделей.
Содержание
Примеры
На примере линейной регрессии
Представьте задачу линейной регрессии. Красные точки представляют исходные данные. Синие линии являются графиками полиномов различной степени M, аппроксимирующих исходные данные.
Как видно из Рис. 1, данные не поддаются линейной зависимости при небольшой степени полинома и по этой причине модель, представленная на данном рисунке, не очень хороша.
На Рис. 2 представлена ситуация, когда выбранная полиномиальная функция подходит для описания исходных данных.
Рис. 3 иллюстрирует случай, когда высокая степень полинома ведет к тому, что модель слишком заточена на данные обучающего датасета.
На примере логистической регрессии
Представьте задачу классификации размеченных точек. Красные точки представляют данные класса 1. Голубые круглые точки — класса 2. Синие линии являются представлением различных моделей, которыми производится классификация данных.
Рис. 4 показывает результат использования слишком простой модели для представленного датасета
Кривые обучения
Кривая обучения — графическое представление того, как изменение меры обученности (по вертикальной оси) зависит от определенной единицы измерения опыта (по горизонтальной оси)[1]. Например, в примерах ниже представлена зависимость средней ошибки от объема датасета.
Кривые обучения при переобучении
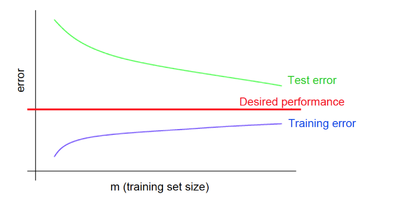
При переобучении небольшая средняя ошибка на обучающей выборке не обеспечивает такую же малую ошибку на тестовой выборке.
Рис. 7 демонстрирует зависимость средней ошибки для обучающей и тестовой выборок от объема датасета при переобучении.
Кривые обучения при недообучении
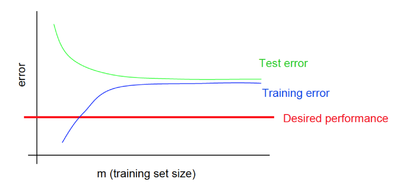
При недообучении независимо от объема обучающего датасета как на обучающей выборке, так и на тестовой выборке небольшая средняя ошибка не достигается.
Рис. 8 демонстрирует зависимость средней ошибки для обучающей и тестовой выборок от объема датасета при недообучении.
High variance и high bias
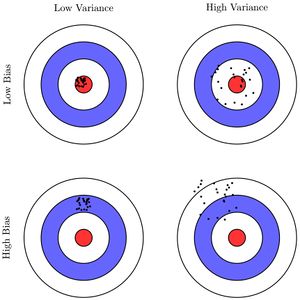
Bias — ошибка неверных предположений в алгоритме обучения. Высокий bias может привести к недообучению.
Variance — ошибка, вызванная большой чувствительностью к небольшим отклонениям в тренировочном наборе. Высокая дисперсия может привести к переобучению.
При использовании нейронных сетей variance увеличивается, а bias уменьшается с увеличением количества скрытых слоев.
Для устранения high variance и high bias можно использовать смеси и ансамбли. Например, можно составить ансамбль (boosting) из нескольких моделей с высоким bias и получить модель с небольшим bias. В другом случае при bagging соединяются несколько моделей с низким bias, а результирующая модель позволяет уменьшить variance.
Дилемма bias–variance
Дилемма bias–variance — конфликт в попытке одновременно минимизировать bias и variance, тогда как уменьшение одного из негативных эффектов, приводит к увеличению другого. Данная дилемма проиллюстрирована на Рис 10.
При небольшой сложности модели мы наблюдаем high bias. При усложнении модели bias уменьшается, но variance увеличится, что приводит к проблеме high variance.
Возможные решения
Возможные решения при переобучении
- Увеличение количества данных в наборе;
- Уменьшение количества параметров модели;
- Добавление регуляризации / увеличение коэффициента регуляризации.
Возможные решения при недообучении
- Добавление новых параметров модели;
- Использование для описания модели функций с более высокой степенью;
- Уменьшение коэффициента регуляризации.
См. также
- Модель алгоритма и ее выбор
- Оценка качества в задачах классификации и регрессии[на 28.01.19 не создан]
- Оценка качества в задаче кластеризации
Примечания
Источники информации
- The Problem of Overfitting on Coursera, Andrew Ng
- Overfitting: when accuracy measure goes wrong
- The Problem of Overfitting Data
- Overfitting in Machine Learning
- Overfitting - статься на Википедии
- Переобучение - вводная статься на MachineLearning.ru
- The Problem of Overfitting - курс Andrew Ng
- Hastie, T., Tibshirani, R., Friedman, J. The Elements of Statistical Learning, 2nd edition. — Springer, 2009. — 533 p.
- Vapnik V.N. Statistical learning theory. — N.Y.: John Wiley & Sons, Inc., 1998.
- Воронцов, К. В. Комбинаторная теория надёжности обучения по прецедентам: Дис. док. физ.-мат. наук: 05-13-17. — Вычислительный центр РАН, 2010. — 271 с.