Обучение с подкреплением — различия между версиями
м (rollbackEdits.php mass rollback) |
|||
| (не показано 29 промежуточных версий 4 участников) | |||
| Строка 1: | Строка 1: | ||
| + | {{Определение | ||
| + | |definition= | ||
| + | '''Обучение с подкреплением''' (англ. ''reinforcement learning'') {{---}} способ машинного обучения, при котором система обучается, взаимодействуя с некоторой средой. | ||
| + | }} | ||
| + | |||
== Обучение с подкреплением == | == Обучение с подкреплением == | ||
| − | + | ||
| − | Алгоритмы с частичным обучением пытаются найти | + | В обучении с подкреплением существует агент (''agent'') взаимодействует с окружающей средой (''environment''), предпринимая действия (''actions''). Окружающая среда дает награду (''reward'') за эти действия, а агент продолжает их предпринимать. |
| + | |||
| + | Алгоритмы с частичным обучением пытаются найти стратегию, приписывающую состояниям (''states'') окружающей среды действия, одно из которых может выбрать агент в этих состояниях. | ||
Среда обычно формулируется как [http://en.wikipedia.org/wiki/Markov_decision_process марковский процесс принятия решений] (МППР) с конечным множеством состояний, и в этом смысле алгоритмы обучения с подкреплением тесно связаны с динамическим программированием. | Среда обычно формулируется как [http://en.wikipedia.org/wiki/Markov_decision_process марковский процесс принятия решений] (МППР) с конечным множеством состояний, и в этом смысле алгоритмы обучения с подкреплением тесно связаны с динамическим программированием. | ||
Вероятности выигрышей и перехода состояний в МППР обычно являются величинами случайными, но стационарными в рамках задачи. | Вероятности выигрышей и перехода состояний в МППР обычно являются величинами случайными, но стационарными в рамках задачи. | ||
| − | При обучении с подкреплением, в отличии от | + | При обучении с подкреплением, в отличии от обучения с учителем, не предоставляются верные пары "входные данные-ответ", а принятие субоптимальнх решений (дающих локальный экстремум) не ограничивается явно. |
| − | Обучение с подкреплением пытается найти компромисс между исследованием неизученных областей и применением имеющихся знаний. | + | Обучение с подкреплением пытается найти компромисс между исследованием неизученных областей и применением имеющихся знаний (''exploration vs exploitation''). |
| − | Баланс изучения-применения при обучении с подкреплением исследуется в задаче [http://en.wikipedia.org/wiki/Multi-armed_bandit | + | Баланс изучения-применения при обучении с подкреплением исследуется в задаче [http://en.wikipedia.org/wiki/Multi-armed_bandit о многоруком бандите]. |
| − | Формально простейшая модель обучения с подкреплением состоит из | + | Формально простейшая модель обучения с подкреплением состоит из: |
| − | + | * множества состояний окружения (''states'') <tex>S</tex>; | |
| − | + | * множества действий (''actions'') <tex>A</tex>; | |
| − | + | * множества вещественнозначных скалярных "выигрышей" (''rewards''). | |
В произвольный момент времени <tex>t</tex> агент характеризуется состоянием <tex>s_t \in S</tex> и множеством возможных действий <tex>A(s_t)</tex>. | В произвольный момент времени <tex>t</tex> агент характеризуется состоянием <tex>s_t \in S</tex> и множеством возможных действий <tex>A(s_t)</tex>. | ||
| Строка 19: | Строка 26: | ||
Основываясь на таком взаимодействии с окружающей средой, агент, обучающийся с подкреплением, должен выработать стратегию <tex>\pi: S \to A</tex>, которая максимизирует величину <tex>R=r_0 + r_1+\cdots+r_n</tex> в случае МППР, имеющего терминальное состояние, или величину: | Основываясь на таком взаимодействии с окружающей средой, агент, обучающийся с подкреплением, должен выработать стратегию <tex>\pi: S \to A</tex>, которая максимизирует величину <tex>R=r_0 + r_1+\cdots+r_n</tex> в случае МППР, имеющего терминальное состояние, или величину: | ||
| − | ::<tex>R=\sum_t \gamma^t r_t</tex> | + | ::<tex>R=\sum_t \gamma^t r_t</tex>, |
| − | для МППР без терминальных состояний (где <tex>0 \leq \gamma \leq 1</tex> - дисконтирующий множитель для "предстоящего выигрыша"). | + | для МППР без терминальных состояний (где <tex>0 \leq \gamma \leq 1</tex> {{---}} дисконтирующий множитель для "предстоящего выигрыша"). |
Таким образом, обучение с подкреплением особенно хорошо подходит для решения задач, связанных с выбором между долгосрочной и краткосрочной выгодой. | Таким образом, обучение с подкреплением особенно хорошо подходит для решения задач, связанных с выбором между долгосрочной и краткосрочной выгодой. | ||
| Строка 27: | Строка 34: | ||
=== Постановка задачи обучения с подкреплением === | === Постановка задачи обучения с подкреплением === | ||
| − | [[File:RL.png|thumb| | + | [[File:RL.png|thumb|link=https://econophysica.ru/services/machine-learning/|Взаимодействие агента со средой]] |
| − | <tex>S</tex> - множество состояний среды | + | <tex>S</tex> {{---}} множество состояний среды |
Игра агента со средой: | Игра агента со средой: | ||
| − | * инициализация стратегии <tex>\pi_1(a|s)</tex> и состояния среды <tex>s_1</tex> | + | * инициализация стратегии <tex>\pi_1(a | s)</tex> и состояния среды <tex>s_1</tex>; |
| − | * для всех <tex>t = 1 \ldots T</tex> | + | * для всех <tex>t = 1 \ldots T</tex>: |
| − | ** агент выбирает действие <tex>a_t ∼ \pi_t(a|s_t)</tex> | + | ** агент выбирает действие <tex>a_t ∼ \pi_t(a | s_t)</tex>; |
| − | ** среда генерирует награду <tex>r_{t + 1} ∼ p(r|a_t, s_t)</tex> и новое состояние <tex>s_{t + 1} ∼ p(s|a_t, s_t)</tex> | + | ** среда генерирует награду <tex>r_{t + 1} ∼ p(r | a_t, s_t)</tex> и новое состояние <tex>s_{t + 1} ∼ p(s | a_t, s_t)</tex>; |
| − | ** агент корректирует стратегию <tex>\pi_{t + 1}(a|s)</tex> | + | ** агент корректирует стратегию <tex>\pi_{t + 1}(a | s)</tex>. |
Это марковский процесс принятия решений (МППР), если | Это марковский процесс принятия решений (МППР), если | ||
| − | <tex>P(s_{t+1} = s′, r_{t+1} = r | s_t, a_t, r_t, s_{t−1}, a_{t−1}, r_{t−1}, .. ,s_1, a_1) = P(s_{t+1} = s′,r_{t+1} = r | s_t, a_t)</tex> | + | <tex>P(s_{t+1} = s′, r_{t+1} = r | s_t, a_t, r_t, s_{t−1}, a_{t−1}, r_{t−1}, .. ,s_1, a_1) = P(s_{t+1} = s′,r_{t+1} = r | s_t, a_t)</tex>, |
МППР называется финитным, если <tex>|A| < \infty</tex>, <tex>|S| < \infty</tex> | МППР называется финитным, если <tex>|A| < \infty</tex>, <tex>|S| < \infty</tex> | ||
| Строка 48: | Строка 55: | ||
Наивный подход к решению этой задачи подразумевает следующие шаги: | Наивный подход к решению этой задачи подразумевает следующие шаги: | ||
| − | * опробовать все возможные стратегии | + | * опробовать все возможные стратегии; |
| − | * выбрать стратегию с наибольшим ожидаемым выигрышем | + | * выбрать стратегию с наибольшим ожидаемым выигрышем. |
Первая проблема такого подхода заключается в том, что количество доступных стратегий может быть очень велико или бесконечно. | Первая проблема такого подхода заключается в том, что количество доступных стратегий может быть очень велико или бесконечно. | ||
| Строка 63: | Строка 70: | ||
либо ожидаемый выигрыш, при принятии решения <tex>a</tex> в состоянии <tex>s</tex> и дальнейшем соблюдении <tex>\pi</tex>, | либо ожидаемый выигрыш, при принятии решения <tex>a</tex> в состоянии <tex>s</tex> и дальнейшем соблюдении <tex>\pi</tex>, | ||
| − | ::<tex>Q(s, a) = E[R|s, \pi, a]</tex> | + | ::<tex>Q(s, a) = E[R|s, \pi, a]</tex>, |
Если для выбора оптимальной стратегии используется функция полезности <tex>Q</tex>, то оптимальные действия всегда можно выбрать как действия, максимизирующие полезность. | Если для выбора оптимальной стратегии используется функция полезности <tex>Q</tex>, то оптимальные действия всегда можно выбрать как действия, максимизирующие полезность. | ||
| Строка 73: | Строка 80: | ||
либо применить т.н. метод исполнитель-критик, в котором модель делится на две части: критик, оценивающий полезность состояния <tex>V</tex>, и исполнитель, выбирающий подходящее действие в каждом состоянии. | либо применить т.н. метод исполнитель-критик, в котором модель делится на две части: критик, оценивающий полезность состояния <tex>V</tex>, и исполнитель, выбирающий подходящее действие в каждом состоянии. | ||
| − | Имея фиксированную стратегию <tex>\pi</tex>, оценить <tex>E[R|\cdot]</tex> при <tex>\gamma = | + | Имея фиксированную стратегию <tex>\pi</tex>, оценить <tex>E[R|\cdot]</tex> при <tex>\gamma = 1</tex> можно просто усреднив непосредственные выигрыши. |
| − | Наиболее очевидный способ оценки при <tex>\gamma | + | Наиболее очевидный способ оценки при <tex>\gamma \in (0, 1)</tex> {{---}} усреднить суммарный выигрыш после каждого состояния. |
Однако для этого требуется, чтобы МППР достиг терминального состояния (завершился). | Однако для этого требуется, чтобы МППР достиг терминального состояния (завершился). | ||
| − | Поэтому построение искомой оценки при <tex>\gamma | + | Поэтому построение искомой оценки при <tex>\gamma \in (0, 1)</tex> неочевидно. Однако, можно заметить, что <tex>R</tex> образуют рекурсивное уравнение Беллмана: |
| − | ::<tex>E[R|s_t]=r_t + \gamma E[R|s_{t+1}]</tex> | + | ::<tex>E[R|s_t]=r_t + \gamma E[R|s_{t+1}]</tex>, |
| − | Подставляя имеющиеся оценки | + | Подставляя имеющиеся оценки <tex>V</tex> и применяя метод градиентного спуска с квадратичной функцией ошибок, мы приходим к алгоритму [http://en.wikipedia.org/wiki/Temporal_difference_learning обучения с временными воздействиями] (''temporal difference (TD) learning''). |
В простейшем случае и состояния, и действия дискретны и можно придерживаться табличных оценок для каждого состояния. | В простейшем случае и состояния, и действия дискретны и можно придерживаться табличных оценок для каждого состояния. | ||
Другие похожие методы: Адаптивный эвристический критик (Adaptive Heuristic Critic, AHC), [http://en.wikipedia.org/wiki/SARSA SARSA] и Q-обучение ([http://en.wikipedia.org/wiki/Q-Learning Q-learning]). | Другие похожие методы: Адаптивный эвристический критик (Adaptive Heuristic Critic, AHC), [http://en.wikipedia.org/wiki/SARSA SARSA] и Q-обучение ([http://en.wikipedia.org/wiki/Q-Learning Q-learning]). | ||
| − | == Задача о многоруком бандите == | + | == Задача о многоруком бандите (''The multi-armed bandit problem'') == |
| − | [[File:bandit.jpg|thumb|Многорукий бандит]] | + | [[File:bandit.jpg|thumb|link=http://toppromotion.ru/blog/seo-category/novyij-algoritm-pod-nazvaniem-%C2%ABmnogorukij-bandit%C2%BB.html|Многорукий бандит]] |
=== Формулировка === | === Формулировка === | ||
| − | <tex>A</tex> {{---}} множество возможных ''действий'' | + | <tex>A</tex> {{---}} множество возможных ''действий'' (ручек автомата), |
| − | <tex>p_a(r)</tex> {{---}} неизвестное распределение ''награды'' <tex>r \in R \forall a \in A</tex> | + | <tex>p_a(r)</tex> {{---}} неизвестное распределение ''награды'' <tex>r \in R</tex> <tex>\forall a \in A</tex>, |
| − | <tex>\pi_t(a)</tex> {{---}} ''стратегия'' агента в момент <tex>t \forall a \in A</tex> | + | <tex>\pi_t(a)</tex> {{---}} ''стратегия'' агента в момент <tex>t</tex> <tex>\forall a \in A</tex>. |
Игра агента со средой: | Игра агента со средой: | ||
| − | * инициализация стратегии <tex>\pi_1(a)</tex> | + | * инициализация стратегии <tex>\pi_1(a)</tex>; |
| − | * для всех <tex>t = 1 \ldots T</tex> | + | * для всех <tex>t = 1 \ldots T</tex>: |
| − | ** агент выбирает действие <tex>a_t ∼ \pi_t(a)</tex> | + | ** агент выбирает действие (ручку) <tex>a_t ∼ \pi_t(a)</tex>; |
| − | ** среда генерирует награду <tex>r_t ∼ p_{a_t}(r)</tex> | + | ** среда генерирует награду <tex>r_t ∼ p_{a_t}(r)</tex>; |
| − | ** агент корректирует стратегию <tex>\pi_{t+1}(a)</tex> | + | ** агент корректирует стратегию <tex>\pi_{t+1}(a)</tex>. |
| − | <tex>Q_t(a) = \frac{\sum^{t}_{i=1}{r_i[a_i = a]}}{\sum^{t}_{i=1}{[a_i = a]}} \rightarrow max </tex> | + | <tex>Q_t(a) = \frac{\sum^{t}_{i=1}{r_i[a_i = a]}}{\sum^{t}_{i=1}{[a_i = a]}} \rightarrow max </tex> {{---}} средняя награда в <i>t</i> играх <br />, |
| − | <tex>Q^∗(a) = \lim \limits_{t \rightarrow \infty} Q_t(a) \rightarrow max </tex> | + | <tex>Q^∗(a) = \lim \limits_{t \rightarrow \infty} Q_t(a) \rightarrow max </tex> {{---}} ценность действия <tex>a</tex>. |
| − | У нас есть автомат {{---}} <tex>N</tex>-рукий бандит, на каждом шаге мы выбираем за какую из <tex>N</tex> | + | У нас есть автомат {{---}} <tex>N</tex>-рукий бандит, на каждом шаге мы выбираем за какую из <tex>N</tex> ручек автомата дернуть, |
т.е. множество действий <tex>A = {1,2 \ldots ,N}</tex>. | т.е. множество действий <tex>A = {1,2 \ldots ,N}</tex>. | ||
| − | Выбор действия <tex>a_t</tex> на шаге <tex>t</tex> влечет награду <tex>R(a_t)</tex> при этом <tex>R(a) \forall a \in A</tex> есть случайная величина, распределение которой неизвестно. | + | Выбор действия <tex>a_t</tex> на шаге <tex>t</tex> влечет награду <tex>R(a_t)</tex> при этом <tex>R(a)</tex> <tex>\forall a \in A</tex> есть случайная величина, распределение которой неизвестно. |
Состояние среды у нас от шага к шагу не меняется, а значит множество состояний <tex>S</tex> тривиально, ни на что не влияет, поэтому его можно проигнорировать. | Состояние среды у нас от шага к шагу не меняется, а значит множество состояний <tex>S</tex> тривиально, ни на что не влияет, поэтому его можно проигнорировать. | ||
| Строка 117: | Строка 124: | ||
Для простоты будем полагать, что каждому действию соответствует некоторое распределение, которое не меняется со временем. Если бы мы знали эти распределения, то очевидная стратегия заключалась бы в том, чтобы подсчитать математическое ожидание для каждого из распределений, выбрать действие с максимальным математическим ожиданием и теперь совершать это действие на каждом шаге. | Для простоты будем полагать, что каждому действию соответствует некоторое распределение, которое не меняется со временем. Если бы мы знали эти распределения, то очевидная стратегия заключалась бы в том, чтобы подсчитать математическое ожидание для каждого из распределений, выбрать действие с максимальным математическим ожиданием и теперь совершать это действие на каждом шаге. | ||
| − | Проблема в том, что распределения неизвестны | + | Проблема в том, что распределения неизвестны, однако можно оценить математическое ожидание некоторой случайной величины <tex>\xi</tex> c неизвестным распределением. Для <tex>K</tex> экспериментов <tex>\xi_k</tex>, оценка математического ожидания это среднее арифметическое результатов экспериментов: |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | <tex>E(\xi) = \frac{1}{K} \sum_{k=1}^{K}{\xi_k} </tex>, | |
| − | + | Задача является модельной для понимания конфликта между ''exploitation''-''exploration''. | |
| − | + | === Жадные и <tex>\epsilon</tex>-жадные стратегии (''greedy & <tex>\epsilon</tex>-greedy'') === | |
| − | === Жадная (greedy) стратегия === | + | ==== Жадная (''greedy'') стратегия ==== |
| − | * <tex>P_a = 0 \forall a \in \{1 \ldots N\} | + | * <tex>P_a = 0</tex> <tex>\forall a \in \{1 \ldots N\} </tex> {{---}} сколько раз было выбрано действие <tex>a</tex>, |
| − | * <tex>Q_a = 0 \forall a \in \{1 \ldots N\} | + | * <tex>Q_a = 0</tex> <tex>\forall a \in \{1 \ldots N\}</tex> {{---}} текущая оценка математического ожидания награды для действия <tex>a</tex>. |
На каждом шаге <tex>t</tex> | На каждом шаге <tex>t</tex> | ||
* Выбираем действие с максимальной оценкой математического ожидания: | * Выбираем действие с максимальной оценкой математического ожидания: | ||
| − | :<tex>a_t = argmax_{a \in A} Q_a </tex> | + | :<tex>a_t = argmax_{a \in A} Q_a </tex>, |
| − | * Выполняем действие <tex>a_t</tex> и получаем награду <tex>R(a_t)</tex> | + | * Выполняем действие <tex>a_t</tex> и получаем награду <tex>R(a_t)</tex>; |
* Обновляем оценку математического ожидания для действия <tex>a_t</tex>: | * Обновляем оценку математического ожидания для действия <tex>a_t</tex>: | ||
| − | :<tex>P_{a_t} = P_{a_t} + 1</tex> | + | :<tex>P_{a_t} = P_{a_t} + 1</tex>, |
| − | :<tex>Q_{a_t} = Q_{a_t} + \frac{1}{P_{a_t}} (R(a_t) − Q_{a_t})</tex> | + | :<tex>Q_{a_t} = Q_{a_t} + \frac{1}{P_{a_t}} (R(a_t) − Q_{a_t})</tex>. |
В чем проблема? | В чем проблема? | ||
| Строка 157: | Строка 158: | ||
Но если награда случайная величина, то единичной попытки будет не достаточно. Поэтому модифицируем жадную стратегию следующим образом: | Но если награда случайная величина, то единичной попытки будет не достаточно. Поэтому модифицируем жадную стратегию следующим образом: | ||
| − | === <tex>\epsilon</tex>-жадная (<tex>\epsilon</tex>-greedy) стратегия === | + | ==== <tex>\epsilon</tex>-жадная (<tex>\epsilon</tex>-''greedy'') стратегия ==== |
| − | [[File:Eps-greedy.png|thumb|313px|Пример. Награда для стратегии с различными <tex>\epsilon</tex>]] | + | [[File:Eps-greedy.png|thumb|313px|link=https://vbystricky.github.io/2017/01/rl_multi_arms_bandits.html|Пример. Награда для стратегии с различными <tex>\epsilon</tex>]] |
| − | Введем параметр <tex>\epsilon \in (0,1)</tex> | + | Введем параметр <tex>\epsilon \in (0,1)</tex>. |
На каждом шаге <tex>t</tex> | На каждом шаге <tex>t</tex> | ||
| − | * Получим значение <tex>\alpha</tex> {{---}} случайной величины равномерно распределенной на отрезке <tex>(0, 1)</tex> | + | * Получим значение <tex>\alpha</tex> {{---}} случайной величины равномерно распределенной на отрезке <tex>(0, 1)</tex>; |
| − | * Если <tex>\alpha \in (0, \epsilon)</tex>, то выберем действие <tex>a_t \in A</tex> случайно и равновероятно, иначе как в жадной стратегии | + | * Если <tex>\alpha \in (0, \epsilon)</tex>, то выберем действие <tex>a_t \in A</tex> случайно и равновероятно, иначе как в жадной стратегии выберем действие с максимальной оценкой математического ожидания; |
| − | * Обновляем оценки так же как в жадной стратегии | + | * Обновляем оценки так же как в жадной стратегии. |
Если <tex>\epsilon = 0</tex>, то это обычная жадная стратегия. Однако если <tex>\epsilon > 0</tex>, то в отличии от жадной стратегии на каждом шаге с вероятностью <tex>\epsilon</tex> присходит "исследование" случайных действий. | Если <tex>\epsilon = 0</tex>, то это обычная жадная стратегия. Однако если <tex>\epsilon > 0</tex>, то в отличии от жадной стратегии на каждом шаге с вероятностью <tex>\epsilon</tex> присходит "исследование" случайных действий. | ||
| − | == Стратегия Softmax == | + | === Стратегия Softmax === |
Основная идея алгоритма ''softmax'' {{---}} уменьшение потерь при исследовании за счёт более редкого выбора действий, которые небольшую награду в прошлом. Чтобы этого добиться для каждого действия вычисляется весовой коэффициент на базе которого происходит выбор действия. Чем больше <tex>Q_t(a)</tex>, тем больше вероятность выбора <tex>a</tex>: | Основная идея алгоритма ''softmax'' {{---}} уменьшение потерь при исследовании за счёт более редкого выбора действий, которые небольшую награду в прошлом. Чтобы этого добиться для каждого действия вычисляется весовой коэффициент на базе которого происходит выбор действия. Чем больше <tex>Q_t(a)</tex>, тем больше вероятность выбора <tex>a</tex>: | ||
| − | <tex>\pi_{t+1}(a) = \frac{exp(Q_t(a) / \tau)}{\sum\limits_{b \in A} {exp(Q_t(b) / \tau)}}</tex> | + | <tex>\pi_{t+1}(a) = \frac{exp(Q_t(a) / \tau)}{\sum\limits_{b \in A} {exp(Q_t(b) / \tau)}}</tex>, |
| − | <tex>\tau \in (0, \infty)</tex> {{---}} параметр, с помощью которого можно настраивать поведение алгоритма. При <tex>\tau \rightarrow \infty</tex> стратегия стремится к равномерной, то есть softmax будет меньше зависеть от значения выигрыша и выбирать действия более равномерно ( | + | <tex>\tau \in (0, \infty)</tex> {{---}} параметр, с помощью которого можно настраивать поведение алгоритма. |
| + | |||
| + | При <tex>\tau \rightarrow \infty</tex> стратегия стремится к равномерной, то есть softmax будет меньше зависеть от значения выигрыша и выбирать действия более равномерно (exploration). | ||
| + | |||
| + | При <tex>\tau \rightarrow 0</tex> стратегия стремится к жадной, то есть алгоритм будет больше ориентироваться на известный средний выигрыш действий (exploitation). | ||
Экспонента используется для того, чтобы данный вес был ненулевым даже у действий, награда от которых пока нулевая. | Экспонента используется для того, чтобы данный вес был ненулевым даже у действий, награда от которых пока нулевая. | ||
| Строка 183: | Строка 188: | ||
Эвристика: параметр <tex>\tau</tex> имеет смысл уменьшать со временем. | Эвристика: параметр <tex>\tau</tex> имеет смысл уменьшать со временем. | ||
| − | == Метод UCB (upper confidence bound) == | + | === Метод UCB (''upper confidence bound'') === |
Предыдущие алгоритмы при принятии решения используют данные о среднем выигрыше. Проблема в том, что если действие даёт награду с какой-то вероятностью, то данные от наблюдений получаются шумные и мы можем неправильно определять самое выгодное действие. | Предыдущие алгоритмы при принятии решения используют данные о среднем выигрыше. Проблема в том, что если действие даёт награду с какой-то вероятностью, то данные от наблюдений получаются шумные и мы можем неправильно определять самое выгодное действие. | ||
| − | Алгоритм верхнего доверительного интервала ('' | + | Алгоритм верхнего доверительного интервала (''upper confidence bound'' или UCB) {{---}} семейство алгоритмов, которые пытаются решить эту проблему, используя при выборе данные не только о среднем выигрыше, но и о том, насколько можно доверять значениям выигрыша. |
Также как ''softmax'' в UCB при выборе действия используется весовой коэффициент, который представляет собой верхнюю границу доверительного интервала (upper confidence bound) значения выигрыша: | Также как ''softmax'' в UCB при выборе действия используется весовой коэффициент, который представляет собой верхнюю границу доверительного интервала (upper confidence bound) значения выигрыша: | ||
| − | <tex>\pi_{t+1}(a) = Q_t(a) + b_a</tex> | + | <tex>\pi_{t+1}(a) = Q_t(a) + b_a</tex>, |
<tex>b_a = \sqrt{\frac{2 \ln{\sum_a P_a}}{P_a}} </tex> {{---}} бонусное значение, которые показывает, насколько недоисследовано действие по сравнению с остальными. | <tex>b_a = \sqrt{\frac{2 \ln{\sum_a P_a}}{P_a}} </tex> {{---}} бонусное значение, которые показывает, насколько недоисследовано действие по сравнению с остальными. | ||
| Строка 207: | Строка 212: | ||
Таким образом, алгоритм это функция качества от состояния и действия: | Таким образом, алгоритм это функция качества от состояния и действия: | ||
| − | :<tex>Q: S \times A \to \mathbb{R}</tex> | + | :<tex>Q: S \times A \to \mathbb{R}</tex>, |
Перед обучением <tex>Q</tex> инициализируется случайными значениями. После этого в каждый момент времени <tex>t</tex> агент выбирает действие <tex>a_t</tex>, получает награду <tex>r_t</tex>, переходит в новое состояние <tex>s_{t+1}</tex>, которое может зависеть от предыдущего состояния <tex>s_t</tex> и выбранного действия, и обновляет функцию <tex>Q</tex>. Обновление функции использует взвешенное среднее между старым и новым значениями: | Перед обучением <tex>Q</tex> инициализируется случайными значениями. После этого в каждый момент времени <tex>t</tex> агент выбирает действие <tex>a_t</tex>, получает награду <tex>r_t</tex>, переходит в новое состояние <tex>s_{t+1}</tex>, которое может зависеть от предыдущего состояния <tex>s_t</tex> и выбранного действия, и обновляет функцию <tex>Q</tex>. Обновление функции использует взвешенное среднее между старым и новым значениями: | ||
| Строка 219: | Строка 224: | ||
=== Aлгоритм Q-learning === | === Aлгоритм Q-learning === | ||
| − | [[File:Q-Learning.png|thumb|313px|Процесс Q-обучения]] | + | [[File:Q-Learning.png|thumb|313px|link=https://en.wikipedia.org/wiki/Q-learning|Процесс Q-обучения]] |
| − | * <tex>S</tex> — множество состояний | + | * <tex>S</tex> — множество состояний, |
| − | * <tex>A</tex> — множество действий | + | * <tex>A</tex> — множество действий, |
| − | * <tex>R = S \times A \rightarrow \mathbb{R}</tex> | + | * <tex>R = S \times A \rightarrow \mathbb{R}</tex> {{---}} функция награды, |
| − | * <tex>T = S \times A \rightarrow S</tex> | + | * <tex>T = S \times A \rightarrow S</tex> {{---}} функция перехода, |
| − | * <tex>\alpha \in [0, 1]</tex> | + | * <tex>\alpha \in [0, 1]</tex> {{---}} learning rate (обычно 0.1), чем он выше, тем сильнее агент доверяет новой информации, |
| − | * <tex>\gamma \in [0, 1]</tex> | + | * <tex>\gamma \in [0, 1]</tex> {{---}} discounting factor, чем он меньше, тем меньше агент задумывается о выгоде от будущих своих действий. |
'''fun''' Q-learning(<tex>S, A, R, T, \alpha, \gamma</tex>): | '''fun''' Q-learning(<tex>S, A, R, T, \alpha, \gamma</tex>): | ||
'''for''' <tex> s \in S</tex>: | '''for''' <tex> s \in S</tex>: | ||
'''for''' <tex> a \in A</tex>: | '''for''' <tex> a \in A</tex>: | ||
| − | Q | + | Q(s, a) = rand() |
| − | '''while''' Q | + | '''while''' Q is not converged: |
s = <tex> \forall s \in S</tex> | s = <tex> \forall s \in S</tex> | ||
| − | '''while''' s | + | '''while''' s is not terminal: |
<tex>\pi(s) = argmax_{a}{Q(s, a)}</tex> | <tex>\pi(s) = argmax_{a}{Q(s, a)}</tex> | ||
a = <tex>\pi(s)</tex> | a = <tex>\pi(s)</tex> | ||
r = R(s, a) | r = R(s, a) | ||
s' = T(s, a) | s' = T(s, a) | ||
| − | <tex>Q | + | <tex>Q(s', a) = (1 - \alpha) Q(s', a) + \alpha (r + \gamma \max\limits_{a'}{Q(s', a')})</tex> |
s = s' | s = s' | ||
return Q | return Q | ||
| − | |||
== Ссылки == | == Ссылки == | ||
*[http://en.wikipedia.org/wiki/Reinforcement_learning Wikipedia: Reinforcement learning] | *[http://en.wikipedia.org/wiki/Reinforcement_learning Wikipedia: Reinforcement learning] | ||
| + | *[https://login.cs.utexas.edu/sites/default/files/legacy_files/research/documents/1%20intro%20up%20to%20RL%3ATD.pdf Sutton, Richard S., and Andrew G. Barto. Introduction to reinforcement learning. Vol. 135. Cambridge: MIT press, 1998.] | ||
| + | *[https://web.stanford.edu/class/psych209/Readings/SuttonBartoIPRLBook2ndEd.pdf Sutton R. S., Barto A. G. Reinforcement learning: An introduction. – 2011.] | ||
*[http://www.machinelearning.ru/wiki/index.php?title=%D0%9E%D0%B1%D1%83%D1%87%D0%B5%D0%BD%D0%B8%D0%B5_%D1%81_%D0%BF%D0%BE%D0%B4%D0%BA%D1%80%D0%B5%D0%BF%D0%BB%D0%B5%D0%BD%D0%B8%D0%B5%D0%BC Обучение с подкреплением] | *[http://www.machinelearning.ru/wiki/index.php?title=%D0%9E%D0%B1%D1%83%D1%87%D0%B5%D0%BD%D0%B8%D0%B5_%D1%81_%D0%BF%D0%BE%D0%B4%D0%BA%D1%80%D0%B5%D0%BF%D0%BB%D0%B5%D0%BD%D0%B8%D0%B5%D0%BC Обучение с подкреплением] | ||
* [https://en.wikipedia.org/wiki/Multi-armed_bandit Многорукий бандит] | * [https://en.wikipedia.org/wiki/Multi-armed_bandit Многорукий бандит] | ||
| Строка 254: | Строка 260: | ||
* [https://en.wikipedia.org/wiki/Q-learning Q-learning] | * [https://en.wikipedia.org/wiki/Q-learning Q-learning] | ||
* [https://medium.freecodecamp.org/an-introduction-to-q-learning-reinforcement-learning-14ac0b4493cc An introduction to Q-Learning: reinforcement learning] | * [https://medium.freecodecamp.org/an-introduction-to-q-learning-reinforcement-learning-14ac0b4493cc An introduction to Q-Learning: reinforcement learning] | ||
| + | |||
| + | [[Категория: Машинное обучение]] | ||
| + | [[Категория: Обучение с подкреплением]] | ||
Текущая версия на 19:13, 4 сентября 2022
| Определение: |
| Обучение с подкреплением (англ. reinforcement learning) — способ машинного обучения, при котором система обучается, взаимодействуя с некоторой средой. |
Содержание
Обучение с подкреплением
В обучении с подкреплением существует агент (agent) взаимодействует с окружающей средой (environment), предпринимая действия (actions). Окружающая среда дает награду (reward) за эти действия, а агент продолжает их предпринимать.
Алгоритмы с частичным обучением пытаются найти стратегию, приписывающую состояниям (states) окружающей среды действия, одно из которых может выбрать агент в этих состояниях.
Среда обычно формулируется как марковский процесс принятия решений (МППР) с конечным множеством состояний, и в этом смысле алгоритмы обучения с подкреплением тесно связаны с динамическим программированием. Вероятности выигрышей и перехода состояний в МППР обычно являются величинами случайными, но стационарными в рамках задачи.
При обучении с подкреплением, в отличии от обучения с учителем, не предоставляются верные пары "входные данные-ответ", а принятие субоптимальнх решений (дающих локальный экстремум) не ограничивается явно. Обучение с подкреплением пытается найти компромисс между исследованием неизученных областей и применением имеющихся знаний (exploration vs exploitation). Баланс изучения-применения при обучении с подкреплением исследуется в задаче о многоруком бандите.
Формально простейшая модель обучения с подкреплением состоит из:
- множества состояний окружения (states) ;
- множества действий (actions) ;
- множества вещественнозначных скалярных "выигрышей" (rewards).
В произвольный момент времени агент характеризуется состоянием и множеством возможных действий . Выбирая действие , он переходит в состояние и получает выигрыш . Основываясь на таком взаимодействии с окружающей средой, агент, обучающийся с подкреплением, должен выработать стратегию , которая максимизирует величину в случае МППР, имеющего терминальное состояние, или величину:
- ,
для МППР без терминальных состояний (где — дисконтирующий множитель для "предстоящего выигрыша").
Таким образом, обучение с подкреплением особенно хорошо подходит для решения задач, связанных с выбором между долгосрочной и краткосрочной выгодой.
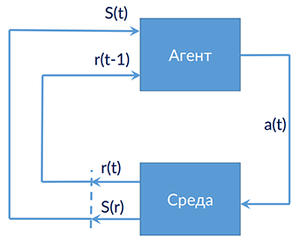
Постановка задачи обучения с подкреплением
— множество состояний среды
Игра агента со средой:
- инициализация стратегии и состояния среды ;
- для всех :
- агент выбирает действие ;
- среда генерирует награду и новое состояние ;
- агент корректирует стратегию .
Это марковский процесс принятия решений (МППР), если ,
МППР называется финитным, если ,
Алгоритмы
Теперь, когда была определена функция выигрыша, нужно определить алгоритм, который будет использоваться для нахождения стратегии, обеспечивающей наилучший результат.
Наивный подход к решению этой задачи подразумевает следующие шаги:
- опробовать все возможные стратегии;
- выбрать стратегию с наибольшим ожидаемым выигрышем.
Первая проблема такого подхода заключается в том, что количество доступных стратегий может быть очень велико или бесконечно. Вторая проблема возникает, если выигрыши стохастические — чтобы точно оценить выигрыш от каждой стратегии потребуется многократно применить каждую из них. Этих проблем можно избежать, если допустить некоторую структуризацию и, возможно, позволить результатам, полученным от пробы одной стратегии, влиять на оценку для другой. Двумя основными подходами для реализации этих идей являются оценка функций полезности и прямая оптимизация стратегий.
Подход с использованием функции полезности использует множество оценок ожидаемого выигрыша только для одной стратегии (либо текущей, либо оптимальной). При этом пытаются оценить либо ожидаемый выигрыш, начиная с состояния , при дальнейшем следовании стратегии ,
- ,
либо ожидаемый выигрыш, при принятии решения в состоянии и дальнейшем соблюдении ,
- ,
Если для выбора оптимальной стратегии используется функция полезности , то оптимальные действия всегда можно выбрать как действия, максимизирующие полезность.
Если же мы пользуемся функцией , необходимо либо иметь модель окружения в виде вероятностей , что позволяет построить функцию полезности вида
- ,
либо применить т.н. метод исполнитель-критик, в котором модель делится на две части: критик, оценивающий полезность состояния , и исполнитель, выбирающий подходящее действие в каждом состоянии.
Имея фиксированную стратегию , оценить при можно просто усреднив непосредственные выигрыши. Наиболее очевидный способ оценки при — усреднить суммарный выигрыш после каждого состояния. Однако для этого требуется, чтобы МППР достиг терминального состояния (завершился).
Поэтому построение искомой оценки при неочевидно. Однако, можно заметить, что образуют рекурсивное уравнение Беллмана:
- ,
Подставляя имеющиеся оценки и применяя метод градиентного спуска с квадратичной функцией ошибок, мы приходим к алгоритму обучения с временными воздействиями (temporal difference (TD) learning). В простейшем случае и состояния, и действия дискретны и можно придерживаться табличных оценок для каждого состояния.
Другие похожие методы: Адаптивный эвристический критик (Adaptive Heuristic Critic, AHC), SARSA и Q-обучение (Q-learning).
Задача о многоруком бандите (The multi-armed bandit problem)
Формулировка
— множество возможных действий (ручек автомата),
— неизвестное распределение награды ,
— стратегия агента в момент .
Игра агента со средой:
- инициализация стратегии ;
- для всех :
- агент выбирает действие (ручку) ;
- среда генерирует награду ;
- агент корректирует стратегию .
— средняя награда в t играх
,
— ценность действия .
У нас есть автомат — -рукий бандит, на каждом шаге мы выбираем за какую из ручек автомата дернуть, т.е. множество действий .
Выбор действия на шаге влечет награду при этом есть случайная величина, распределение которой неизвестно.
Состояние среды у нас от шага к шагу не меняется, а значит множество состояний тривиально, ни на что не влияет, поэтому его можно проигнорировать.
Для простоты будем полагать, что каждому действию соответствует некоторое распределение, которое не меняется со временем. Если бы мы знали эти распределения, то очевидная стратегия заключалась бы в том, чтобы подсчитать математическое ожидание для каждого из распределений, выбрать действие с максимальным математическим ожиданием и теперь совершать это действие на каждом шаге.
Проблема в том, что распределения неизвестны, однако можно оценить математическое ожидание некоторой случайной величины c неизвестным распределением. Для экспериментов , оценка математического ожидания это среднее арифметическое результатов экспериментов:
,
Задача является модельной для понимания конфликта между exploitation-exploration.
Жадные и -жадные стратегии (greedy & -greedy)
Жадная (greedy) стратегия
- — сколько раз было выбрано действие ,
- — текущая оценка математического ожидания награды для действия .
На каждом шаге
- Выбираем действие с максимальной оценкой математического ожидания:
- ,
- Выполняем действие и получаем награду ;
- Обновляем оценку математического ожидания для действия :
- ,
- .
В чем проблема?
Пусть у нас есть "двурукий" бандит. Первая ручка всегда выдаёт награду равную 1, вторая всегда выдаёт 2. Действуя согласно жадной стратегии мы дёрнем в начале первую ручку, так как в начале оценки математических ожиданий равны нулю, увеличим её оценку до . В дальнейшем всегда будем выбирать первую ручку, а значит на каждом шаге будем получать на 1 меньше, чем могли бы.
В данном случае достаточно попробовать в начале каждую из ручек вместо того, чтобы фокусироваться только на одной. Но если награда случайная величина, то единичной попытки будет не достаточно. Поэтому модифицируем жадную стратегию следующим образом:
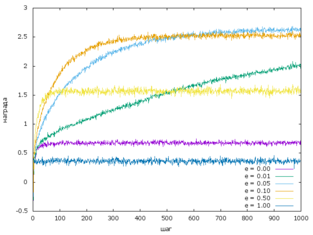
-жадная (-greedy) стратегия
Введем параметр .
На каждом шаге
- Получим значение — случайной величины равномерно распределенной на отрезке ;
- Если , то выберем действие случайно и равновероятно, иначе как в жадной стратегии выберем действие с максимальной оценкой математического ожидания;
- Обновляем оценки так же как в жадной стратегии.
Если , то это обычная жадная стратегия. Однако если , то в отличии от жадной стратегии на каждом шаге с вероятностью присходит "исследование" случайных действий.
Стратегия Softmax
Основная идея алгоритма softmax — уменьшение потерь при исследовании за счёт более редкого выбора действий, которые небольшую награду в прошлом. Чтобы этого добиться для каждого действия вычисляется весовой коэффициент на базе которого происходит выбор действия. Чем больше , тем больше вероятность выбора :
,
— параметр, с помощью которого можно настраивать поведение алгоритма.
При стратегия стремится к равномерной, то есть softmax будет меньше зависеть от значения выигрыша и выбирать действия более равномерно (exploration).
При стратегия стремится к жадной, то есть алгоритм будет больше ориентироваться на известный средний выигрыш действий (exploitation).
Экспонента используется для того, чтобы данный вес был ненулевым даже у действий, награда от которых пока нулевая.
Эвристика: параметр имеет смысл уменьшать со временем.
Метод UCB (upper confidence bound)
Предыдущие алгоритмы при принятии решения используют данные о среднем выигрыше. Проблема в том, что если действие даёт награду с какой-то вероятностью, то данные от наблюдений получаются шумные и мы можем неправильно определять самое выгодное действие.
Алгоритм верхнего доверительного интервала (upper confidence bound или UCB) — семейство алгоритмов, которые пытаются решить эту проблему, используя при выборе данные не только о среднем выигрыше, но и о том, насколько можно доверять значениям выигрыша.
Также как softmax в UCB при выборе действия используется весовой коэффициент, который представляет собой верхнюю границу доверительного интервала (upper confidence bound) значения выигрыша:
,
— бонусное значение, которые показывает, насколько недоисследовано действие по сравнению с остальными.
Доказательство здесь
В отличие от предыдущих алгоритмов UCB не использует в своей работе ни случайные числа для выбора действия, ни параметры, которыми можно влиять на его работу. В начале работы алгоритма каждое из действий выбирается по одному разу (для того чтобы можно было вычислить размер бонуса для всех действий). После этого в каждый момент времени выбирается действие с максимальным значением весового коэффициента.
Несмотря на это отсутствие случайности результаты работы этого алгоритма выглядят довольно шумно по сравнению с остальными. Это происходит из-за того, что данный алгоритм сравнительно часто выбирает недоисследованные действия.
Q-learning
На основе получаемого от среды вознаграждения агент формирует функцию полезности , что впоследствии дает ему возможность уже не случайно выбирать стратегию поведения, а учитывать опыт предыдущего взаимодействия со средой. Одно из преимуществ -обучения — то, что оно в состоянии сравнить ожидаемую полезность доступных действий, не формируя модели окружающей среды. Применяется для ситуаций, которые можно представить в виде МППР.
Таким образом, алгоритм это функция качества от состояния и действия:
- ,
Перед обучением инициализируется случайными значениями. После этого в каждый момент времени агент выбирает действие , получает награду , переходит в новое состояние , которое может зависеть от предыдущего состояния и выбранного действия, и обновляет функцию . Обновление функции использует взвешенное среднее между старым и новым значениями:
- ,
где это награда, полученная при переходе из состояния в состояние , и это скорость обучения ().
Алгоритм заканчивается, когда агент переходит в терминальное состояние .
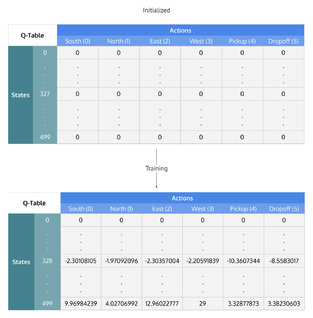
Aлгоритм Q-learning
- — множество состояний,
- — множество действий,
- — функция награды,
- — функция перехода,
- — learning rate (обычно 0.1), чем он выше, тем сильнее агент доверяет новой информации,
- — discounting factor, чем он меньше, тем меньше агент задумывается о выгоде от будущих своих действий.
fun Q-learning(): for : for : Q(s, a) = rand() while Q is not converged: s = while s is not terminal: a = r = R(s, a) s' = T(s, a) s = s' return Q
Ссылки
- Wikipedia: Reinforcement learning
- Sutton, Richard S., and Andrew G. Barto. Introduction to reinforcement learning. Vol. 135. Cambridge: MIT press, 1998.
- Sutton R. S., Barto A. G. Reinforcement learning: An introduction. – 2011.
- Обучение с подкреплением
- Многорукий бандит
- Задача о многоруком бандите
- Обучение с подкреплением (Reinforcement Learning) К.В.Воронцов
- Обзор книги «Bandit Algorithms for Website Optimization»
- Q-learning
- An introduction to Q-Learning: reinforcement learning