Кратчайший путь в ациклическом графе — различия между версиями
Roman (обсуждение | вклад) м |
м (rollbackEdits.php mass rollback) |
||
| (не показано 5 промежуточных версий 3 участников) | |||
| Строка 1: | Строка 1: | ||
| − | Пусть дан ациклический ориентированный взвешенный граф. Требуется найти вес кратчайшего пути из | + | {{Задача |
| − | + | |definition = | |
| + | Пусть дан [[Основные_определения_теории_графов |ациклический ориентированный взвешенный граф]]. Требуется найти вес [[Алгоритм_Дейкстры |кратчайшего пути]] из <tex>u</tex> в <tex>v</tex>. | ||
| + | }} | ||
| + | |||
==Решение== | ==Решение== | ||
| − | Пусть <tex>d</tex> — функция, где <tex>d(i)</tex> — вес кратчайшего пути из <tex>u</tex> в <tex>i</tex>. Ясно, что <tex>d(u)</tex> равен <tex>0</tex>. Пусть <tex>w(i, j)</tex> - вес ребра из <tex>i</tex> в <tex>j</tex>. Будем обходить граф в порядке [[Использование_обхода_в_глубину_для_топологической_сортировки | топологической сортировки]]. Получаем следующие соотношения: <br /> | + | Воспользуемся принципом оптимальности на префиксе.<br /> |
| + | Пусть <tex>d</tex> — функция, где <tex>d(i)</tex> — вес кратчайшего пути из <tex>u</tex> в <tex>i</tex>. Ясно, что <tex>d(u)</tex> равен <tex>0</tex>. Пусть <tex>w(i, j)</tex> {{---}} вес ребра из <tex>i</tex> в <tex>j</tex>. Будем обходить граф в порядке [[Использование_обхода_в_глубину_для_топологической_сортировки | топологической сортировки]]. Получаем следующие соотношения: <br /> | ||
: <tex> d(i) = \min\limits_{\mathop{j:j \rightsquigarrow i}} (d(j) + w(j, i)) </tex> | : <tex> d(i) = \min\limits_{\mathop{j:j \rightsquigarrow i}} (d(j) + w(j, i)) </tex> | ||
| Строка 13: | Строка 17: | ||
<font color=green>//p {{---}} массив индексов вершин графа в порядке топологической сортировки</font> | <font color=green>//p {{---}} массив индексов вершин графа в порядке топологической сортировки</font> | ||
'''for''' i = 1 .. n | '''for''' i = 1 .. n | ||
| − | d[i] = | + | d[i] = <tex>\infty</tex> |
d[u] = 0 <font color=green>// где u {{---}} начальная вершина</font><br /> | d[u] = 0 <font color=green>// где u {{---}} начальная вершина</font><br /> | ||
p = topSort(w) <font color=green>//топологическая сортировка графа</font> | p = topSort(w) <font color=green>//топологическая сортировка графа</font> | ||
| Строка 22: | Строка 26: | ||
==Пример== | ==Пример== | ||
[[Файл:WayAcyclicGraph.png|thumb|right|500px|Граф из примера]] | [[Файл:WayAcyclicGraph.png|thumb|right|500px|Граф из примера]] | ||
| − | Пусть дана матрица смежности графа | + | Пусть дана матрица смежности графа <tex>w</tex> со следующими весами ребер: <br /> |
{| class="wikitable" cellpadding="4" border="1" style="border-collapse: collapse;" | {| class="wikitable" cellpadding="4" border="1" style="border-collapse: collapse;" | ||
|- | |- | ||
| || '''1''' || '''2''' || '''3''' || '''4''' || '''5''' || '''6''' || '''7''' || '''8''' | | || '''1''' || '''2''' || '''3''' || '''4''' || '''5''' || '''6''' || '''7''' || '''8''' | ||
|- | |- | ||
| − | | '''1''' || - || - || - || | + | | '''1''' || - || - || - || - || 2 || - || - || - |
|- | |- | ||
| '''2''' || 1 || - || 1 || - || 4 || 3 || - || - | | '''2''' || 1 || - || 1 || - || 4 || 3 || - || - | ||
| Строка 43: | Строка 47: | ||
| '''8''' || - || - || - || 1 || - || - || - || - | | '''8''' || - || - || - || 1 || - || - || - || - | ||
|} | |} | ||
| − | Требуется найти | + | Требуется найти вес кратчайшего пути из '''2''' в '''4'''. <br /> |
| − | Массив p будет выглядеть следующим образом: <br /> | + | Массив <tex>p</tex> будет выглядеть следующим образом: <br /> |
{| class="wikitable" cellpadding="4" border="1" style="border-collapse: collapse;" | {| class="wikitable" cellpadding="4" border="1" style="border-collapse: collapse;" | ||
|- | |- | ||
| − | | '''1''' || '''2''' || '''3''' || '''4''' || '''5''' || '''6''' || '''7''' || '''8''' | + | | <tex>i</tex> || '''1''' || '''2''' || '''3''' || '''4''' || '''5''' || '''6''' || '''7''' || '''8''' |
|- | |- | ||
| − | | 2 || 3 || 6 || 7 || 1 || 5 || 8 || 4 | + | | <tex>p[i]</tex> || 2 || 3 || 6 || 7 || 1 || 5 || 8 || 4 |
|} | |} | ||
| − | Массив d будет выглядеть следующим образом: <br /> | + | Массив <tex>d</tex> будет выглядеть следующим образом: <br /> |
{| class="wikitable" cellpadding="4" border="1" style="border-collapse: collapse;" | {| class="wikitable" cellpadding="4" border="1" style="border-collapse: collapse;" | ||
|- | |- | ||
| − | | '''1''' || '''2''' || '''3''' || '''4''' || '''5''' || '''6''' || '''7''' || '''8''' | + | | <tex>i</tex> || '''1''' || '''2''' || '''3''' || '''4''' || '''5''' || '''6''' || '''7''' || '''8''' |
|- | |- | ||
| − | | 1 || 0 || 1 || 5 || 3 || 2 || 4 || 4 | + | | <tex>d[i]</tex> || 1 || 0 || 1 || 5 || 3 || 2 || 4 || 4 |
|} | |} | ||
| − | Ответ равен 5. | + | Ответ равен <tex>5</tex>. |
==Альтернативный способ решения== | ==Альтернативный способ решения== | ||
| − | + | Решим задачу, используя [[Обход_в_ширину |обход в ширину]]. Для этого заведем массив, в котором будем хранить веса кратчайших расстояний от начальной вершины до всех остальных. Совершая обход по графу, будем в каждой вершине для всех ее потомков проверять, уменьшится ли вес кратчайшего пути до сына, если пройти через текущую вершину. Если да, то весу кратчайшего расстояния до сына присваиваем значение, равное сумме веса кратчайшего расстояния до текущей вершины и стоимости прохода по ребру между вершиной и ее сыном. | |
| − | + | В силу особенности обхода графа, обновление весов кратчайших путей до сыновей вершины происходит только тогда, когда для нее уже найден оптимальный ответ. | |
| − | В силу особенности обхода графа, | ||
| − | == | + | ==См. также== |
| − | |||
*[[Алгоритм_Флойда_—_Уоршалла |Алгоритм Флойда—Уоршалла]] | *[[Алгоритм_Флойда_—_Уоршалла |Алгоритм Флойда—Уоршалла]] | ||
| − | |||
*[[Алгоритм_Форда-Беллмана |Алгоритм Форда-Беллмана]] | *[[Алгоритм_Форда-Беллмана |Алгоритм Форда-Беллмана]] | ||
==Источники информации== | ==Источники информации== | ||
*[http://www.ics.uci.edu/~eppstein/161/960208.html Алгоритмы поиска кратчайшего пути в графе] | *[http://www.ics.uci.edu/~eppstein/161/960208.html Алгоритмы поиска кратчайшего пути в графе] | ||
| − | + | * [http://en.wikipedia.org/wiki/Optimal_substructure Wikipedia {{---}} Optimal substructure] | |
| − | * [http://en.wikipedia.org/wiki/Optimal_substructure | ||
[[Категория:Дискретная математика и алгоритмы]] | [[Категория:Дискретная математика и алгоритмы]] | ||
[[Категория:Динамическое программирование]] | [[Категория:Динамическое программирование]] | ||
Текущая версия на 19:14, 4 сентября 2022
| Задача: |
| Пусть дан ациклический ориентированный взвешенный граф. Требуется найти вес кратчайшего пути из в . |
Содержание
Решение
Воспользуемся принципом оптимальности на префиксе.
Пусть — функция, где — вес кратчайшего пути из в . Ясно, что равен . Пусть — вес ребра из в . Будем обходить граф в порядке топологической сортировки. Получаем следующие соотношения:
Так как мы обходим граф в порядке топологической сортировки, то на -ом шаге всем ( такие, что существует ребро из в ) уже присвоены оптимальные ответы, и, следовательно, также будет присвоен оптимальный ответ.
Реализация
Реализуем данный алгоритм:
//w — матрица смежности //d — массив кратчайших расстояний //p — массив индексов вершин графа в порядке топологической сортировки for i = 1 .. n d[i] = d[u] = 0 // где u — начальная вершина
p = topSort(w) //топологическая сортировка графа for i = 1 .. n for j: есть ребро из p[i] в j d[j] = min(d[j], d[p[i]] + w[p[i]][j])
Пример
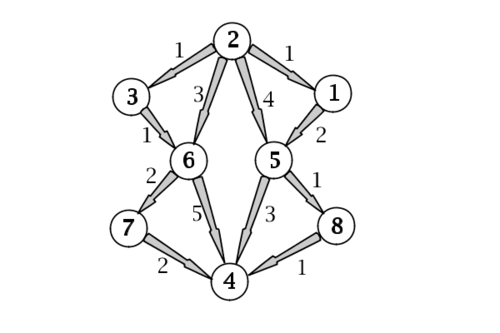
Пусть дана матрица смежности графа со следующими весами ребер:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| 1 | - | - | - | - | 2 | - | - | - |
| 2 | 1 | - | 1 | - | 4 | 3 | - | - |
| 3 | - | - | - | - | - | 1 | - | - |
| 4 | - | - | - | - | - | - | - | - |
| 5 | - | - | - | 3 | - | - | - | 1 |
| 6 | - | - | - | 5 | - | - | 2 | - |
| 7 | - | - | - | 2 | - | - | - | - |
| 8 | - | - | - | 1 | - | - | - | - |
Требуется найти вес кратчайшего пути из 2 в 4.
Массив будет выглядеть следующим образом:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| 2 | 3 | 6 | 7 | 1 | 5 | 8 | 4 |
Массив будет выглядеть следующим образом:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| 1 | 0 | 1 | 5 | 3 | 2 | 4 | 4 |
Ответ равен .
Альтернативный способ решения
Решим задачу, используя обход в ширину. Для этого заведем массив, в котором будем хранить веса кратчайших расстояний от начальной вершины до всех остальных. Совершая обход по графу, будем в каждой вершине для всех ее потомков проверять, уменьшится ли вес кратчайшего пути до сына, если пройти через текущую вершину. Если да, то весу кратчайшего расстояния до сына присваиваем значение, равное сумме веса кратчайшего расстояния до текущей вершины и стоимости прохода по ребру между вершиной и ее сыном. В силу особенности обхода графа, обновление весов кратчайших путей до сыновей вершины происходит только тогда, когда для нее уже найден оптимальный ответ.