List order maintenance — различия между версиями
м (Minor punctuation) |
м (rollbackEdits.php mass rollback) |
||
| (не показаны 22 промежуточные версии 4 участников) | |||
| Строка 1: | Строка 1: | ||
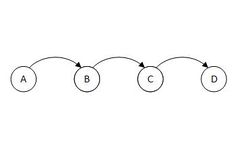
| − | [[Файл:ListABCD.jpg|250px|thumb|right|Для такого списка | + | [[Файл:ListABCD.jpg|250px|thumb|right|Для такого списка операция <tex>\mathrm{order(D,B)}</tex> выдаст <tex>\mathrm{false}</tex>.]] |
| − | '''List order maintance''' ( | + | '''List order maintance''' (рус. <i>поддержание порядка в списке</i>) {{---}} проблема поддержания списка со следующими операциями: |
* <tex>\mathrm{insert(p, q)}</tex> {{---}} вставка нового элемента <tex>p</tex> в список сразу после <tex>q</tex>; | * <tex>\mathrm{insert(p, q)}</tex> {{---}} вставка нового элемента <tex>p</tex> в список сразу после <tex>q</tex>; | ||
* <tex>\mathrm{remove(p)}</tex> {{---}} удаление элемента <tex>p</tex> из списка; | * <tex>\mathrm{remove(p)}</tex> {{---}} удаление элемента <tex>p</tex> из списка; | ||
| − | * <tex>\mathrm{order(p, q)}</tex> {{---}} | + | * <tex>\mathrm{order(p, q)}</tex> {{---}} операция, возвращающая <tex>\mathrm{true}</tex> , если <tex>p</tex> в списке находится до <tex>q</tex> и <tex>\mathrm{false}</tex> иначе. |
| − | Существует реализация структуры, где | + | Существует реализация такой структуры, где <tex>\mathrm{order(p, q)}</tex> выполняется за истинную <tex>O(1)</tex>, а операции добавления и удаления за амортизационную <tex>O(1)</tex>. |
| − | + | Проблема поддержания порядка в списке возникает, к примеру, при реализации [[Персистентные структуры данных|полностью персистентного дерева поиска]]. | |
| − | == Алгоритм | + | == Алгоритм == |
| + | === Идея === | ||
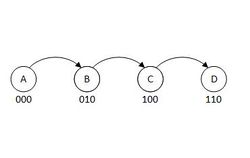
[[Файл:ListABCDwithMarks.jpg|250px|thumb|right|Пример расставления меток для списка, <tex>u=3</tex>.]] | [[Файл:ListABCDwithMarks.jpg|250px|thumb|right|Пример расставления меток для списка, <tex>u=3</tex>.]] | ||
| − | + | Все операции, кроме <tex>\mathrm{order(p,q)}</tex>, за <tex>O(1)</tex> может выполнить обычный [[Список|двусвязный список]], но с его помощью невозможно получить информацию о порядке объектов. Для реализации этой операции каждому узлу можно сопоставить некоторое число так, чтобы все числа строго возрастали от начала к концу списка. Таким образом, эти числа, которые в дальнейшим будут называться <b>метками</b>, задают порядок на элементах списка. | |
| − | |||
| − | + | Ответить на запрос <tex>\mathrm{order(p,q)}</tex> можно за <tex>O(1)</tex>, просто сравнив метки <tex>p</tex> и <tex>q</tex>. Добавление меток никак не влияет на реализацию операции <tex>\mathrm{remove(p)}</tex>. Однако реализацию <tex>\mathrm{insert(p,q)}</tex> потребуется изменить: при добавлении нового элемента <tex>q</tex> после узла <tex>p</tex>, узлу <tex>q</tex> необходимо присвоить метку, которая строго больше предыдущего элемента и строго меньше следующего. В какой-то момент возникнет ситуация, что новой метки не найдётся, тогда метки можно перераспределить среди элементов списка так, чтобы для узла <tex>q</tex> нашлась метка. Далее будет рассмотрен алгоритм, который позволяет эффективно реализовать эту идею. | |
| − | |||
| − | |||
| − | |||
| − | Все метки | + | === Алгоритм за O(logn) === |
| + | ==== Способ хранения меток ==== | ||
| + | Метки будут храниться в виде чисел в двоичной системе счисления. Требуется выбрать такую длину для меток, чтобы перераспределения не случались слишком часто. Если <tex>u</tex> {{---}} длина каждой метки, то для начала пусть <tex>u:n<2^u \leqslant 2n</tex>, где <tex>n</tex> {{---}} количество элементов в списке. Если после добавления элементов какому-то элементу не хватит метки, увеличим <tex>u</tex> на <tex>1</tex> и пересчитаем все метки заново, распределив их равномерно. Заметим, что сразу после перераспределения меток, в среднем, между каждыми двумя элементами списка будет только одна свободная метка, так как при переходе к новому <tex>u</tex> количество меток будет примерно в два раза больше количества элементов списка. Если же после удаления элемента из списка <tex>2^u</tex> станет в <tex>4</tex> раза больше <tex>n</tex>, уменьшим <tex>u</tex> на <tex>1</tex>. Пересчет меток занимает амортизационно <tex>O(1)</tex> по аналогии с [[Динамический массив | саморасширяющимся массивом]]. Однако очевидно, что в таком случае операция добавления за <tex>O(1)</tex> работать не будет, так как, если потребуется добавить между двумя элементами списка больше одного элемента, то новым элементам меток не хватит, и придется провести лишнее перераспределение меток, которое будет рассмотрено ниже. Позже, в доказательстве времени работы, значение <tex>u</tex> будет несколько уточнено. | ||
| + | |||
| + | Все метки будут храниться в [[Сверхбыстрый цифровой бор | цифровом боре]] высоты <tex>u</tex> (там представлены не только используемые метки, а вообще все возможные заданной длины). Введем некоторые обозначения: | ||
| + | * <tex>\mathrm{weight(x)}</tex> {{---}} количество помеченных (используемых) листьев (меток) в поддереве узла <tex>x</tex>; | ||
| + | * <tex>\mathrm{size(x)}</tex> {{---}} количество всех листьев в поддереве <tex>x</tex>; | ||
| + | * <tex>\mathrm{height(x)}</tex> {{---}} высота узла <tex>x</tex> в цифровом боре. | ||
| + | |||
| + | Также в каждом узле дополнительно будет храниться: | ||
| + | * в листьях {{---}} используется ли уже эта метка; | ||
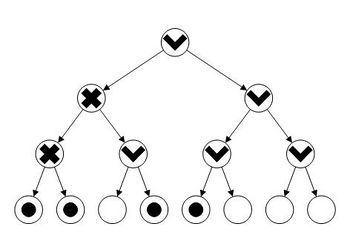
[[Файл:UBitTreeExample.jpg|350px|thumb|right|Пример цифрового бора для меток, где узел с крестиком {{---}} переполненный узел, а с галочкой {{---}} непереполненный для <tex>\alpha=1,5</tex>.]] | [[Файл:UBitTreeExample.jpg|350px|thumb|right|Пример цифрового бора для меток, где узел с крестиком {{---}} переполненный узел, а с галочкой {{---}} непереполненный для <tex>\alpha=1,5</tex>.]] | ||
| + | * в нелистовых узлах {{---}} является ли узел переполненным. | ||
| + | |||
| + | <b>Переполненным</b> назовем узел, для которого для выбранного <tex>\alpha</tex> (<tex>1<\alpha<2</tex>) выполнено <tex>\dfrac{\mathrm{weight(x)}}{\mathrm{size(x)}}>\dfrac{1}{\alpha^{\mathrm{height(x)}}}</tex>. В листьях не хранится наличие переполненности, так как в листьях не может быть переполнения. В крайнем случае для листа: <tex> \dfrac{\mathrm{weight(x)}}{\mathrm{size(x)}} = 1 \ngtr 1 = \dfrac{1}{\alpha^{0}} = \dfrac{1}{\alpha^{\mathrm{height(x)}}} </tex>. | ||
| + | |||
| + | ==== Перераспределение меток ==== | ||
| + | Перераспределение меток потребуется выполнить в случае, когда для нового элемента не будет свободной метки. Пусть требуется выполнить операцию <tex>\mathrm{insert(p, q)}</tex>, но метка, следующая за меткой <tex>q</tex> уже присвоена элементу <tex>z</tex>. Тогда будем подниматься вверх от метки <tex>z</tex> до тех пор, пока не будет найден первый непереполненный узел. Может случиться такое, что на всем пути до корня не встретится ни одного непереполненного узла. Чтобы этого избежать, уточним границы <tex>u</tex> позже. Как только будет найден первый непереполненный узел, переназначим метки в поддереве этого узла так, чтобы они находились друг от друга на одинаковых расстояниях (места точно хватит, так как <tex>\dfrac{\mathrm{weight(x)}}{\mathrm{size(x)}}\leqslant\dfrac{1}{\alpha^{\mathrm{height(x)}}}</tex>, если узел непереполненный). После этого между занятыми метками будет не меньше <tex>\alpha^{\mathrm{height(x)}}</tex> свободных меток. | ||
| + | |||
| + | ==== Доказательство времени работы ==== | ||
| + | Рассмотрим, как часто происходит перераспределение меток: | ||
| + | |||
| + | * Если в поддереве узла было проведено перераспределение меток, то повторное перераспределение меток в поддереве узла <tex>x</tex> потребуется, когда сын этого узла снова переполнится. Если <tex>y</tex> {{---}} сын <tex>x</tex>, то он переполнится, когда <tex>\dfrac{\mathrm{weight(y)}}{\mathrm{size(y)}}>\dfrac{1}{\alpha^{\mathrm{height(x) - 1}}}</tex>. Чтобы это произошло, требуется, чтобы было сделано еще добавлений: | ||
| + | |||
| + | <center> | ||
| + | <tex>\mathrm{size(y)} \cdot (\dfrac{1}{\alpha^{\mathrm{height(x) - 1}}} - \dfrac{1}{\alpha^{\mathrm{height(x)}}}) = \mathrm{size(y)} \cdot \dfrac{\alpha - 1}{\alpha^{\mathrm{height(x)}}}</tex>; | ||
| + | </center> | ||
| + | |||
| + | |||
| + | * С другой стороны, следующее перераспределение меток произойдет, когда <tex>\mathrm{weight(x)}</tex> станет больше | ||
| + | |||
| + | <center> | ||
| + | <tex>\dfrac{\mathrm{size(x)}}{\alpha^{\mathrm{height(x)}}} = \dfrac{2\mathrm{size(y)}}{\alpha^{\mathrm{height(x)}}} </tex>. | ||
| + | </center> | ||
| − | |||
| − | |||
| − | |||
| − | + | Получается, что за <tex>\dfrac{2\mathrm{size(y)}}{\alpha^{\mathrm{height(x)}}} </tex> операций перераспределения меток требуется сделать <tex>\mathrm{size(y)} \cdot \dfrac{\alpha - 1}{\alpha^{\mathrm{height(x)}}}</tex> операций добавления. Используя [[Амортизационный анализ | метод предоплаты]], видим, что если за каждую операцию добавления брать <tex>\dfrac{2}{\alpha-1}</tex> монет, то за добавления накопится достаточное количество монет, чтобы расплатиться за следующую операцию перераспределения в узле <tex>x</tex>. | |
| − | + | Однако таким образом требуется платить за каждый уровень, а количество уровней (бит) равно <tex>u</tex>. Тогда амортизированная стоимость добавления составляет <tex>O(u)</tex>. | |
| − | + | Для того, чтобы на пути к корню точно встретился непереполненный узел, требуется уточнить границы <tex>u</tex>: <tex>\dfrac{\mathrm{weight(root)}}{\mathrm{size(root)}} < \dfrac{1}{\alpha^{\mathrm{height(root)}}} \Rightarrow \dfrac{n}{2^u} < \dfrac{1}{\alpha ^u} \Rightarrow u \geqslant \log_{\frac{ 2}{\alpha}} n</tex>. Тогда операция добавления работает за <tex>O(\log n)</tex>. | |
| − | == Алгоритм за O(1) == | + | === Алгоритм за O(1) === |
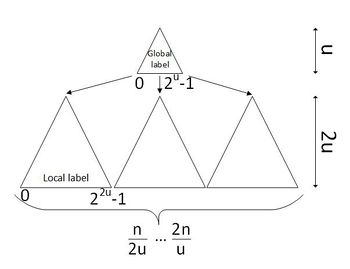
[[Файл:GlobalandLocalLabelstoConst.jpg|350px|thumb|right|y-fast-tree для меток.]] | [[Файл:GlobalandLocalLabelstoConst.jpg|350px|thumb|right|y-fast-tree для меток.]] | ||
| − | + | Предыдущий алгоритм работает за логарифм из-за того, что слишком часто приходится перераспределять метки. Используем <tex>\mathrm{y}{-}\mathrm{fast}{-}\mathrm{trie}</tex> (модифицированный цифровой бор), чтобы улучшить время работы операции добавления до <tex>O(1)</tex>. | |
| + | |||
| + | У каждого элемента списка будет две метки: глобальная и локальная. Глобальная задает блок, локальная {{---}} положение элемента внутри блока. Описание взаимодействия с метками: | ||
| + | |||
| + | * <b>локальные метки</b> внутри каждого блока каждому элементу от <tex>0</tex> до <tex>2^{2u-1}</tex> будут жадно присвоены. Стоит заметить, что внутри блока никогда не будет проблемы, что кому-то не хватит метки или придется сделать перераспределение меток, так как, если каждый раз в качестве метки брать среднее значение, то для того, чтобы был конфликт из-за меток, нужно больше, чем <tex>2u</tex> ключей (противоречит условию); | ||
| + | * <b>глобальные метки</b> будут организованы в структуру, использовавшуюся в реализации операции за логарифмическое время. Глобальные метки для блоков придется менять, когда один из блоков переполнился. Тогда блок будет разделен на два, метка второму будет присвоена методом, описанным выше (поднимемся до первого непереполненного). Каждый блок будет иметь <tex>u</tex> занятых меток. Аналогично, когда в каком-то блок становится слишком мало ключей, он будет слит с соседним. | ||
| + | |||
| + | Внутри блоков присваиваются ключи за <tex>O(1)</tex>, а аналогичный приведенному выше анализ показывает, что к перераспределению глобальных меток приводит<tex>\Omega(u)</tex> изменений локальных меток. За эти изменения будет накоплено <tex>O(u)</tex> монет для изменения глобальных меток, тогда операция добавления работает за константное время. | ||
== Использование памяти == | == Использование памяти == | ||
| − | + | Выбор <tex>\alpha</tex> сильно влияет на реализацию структуры, так как <tex>u</tex> зависит от выбранной <tex>\alpha</tex>. С увеличением <tex>\alpha</tex>, уменьшается стоимость операции добавления (количество монет, которые надо брать: <tex>\dfrac{2}{\alpha-1}</tex>), но увеличивается <tex>u</tex>, значит, требуется больше памяти, а, уменьшая <tex>\alpha</tex>, получаем выигрыш в памяти, но проигрыш во времени операции добавления. Так как для реализации структуры используется <tex>\mathrm{y}{-}\mathrm{fast}{-}\mathrm{trie}</tex>, требуется <tex>O(n)</tex> памяти. | |
== Послесловие == | == Послесловие == | ||
| Строка 59: | Строка 92: | ||
== Источники информации == | == Источники информации == | ||
| − | * [https://www.lektorium.tv/lecture/14321 Lectorium {{---}} | + | * [https://www.lektorium.tv/lecture/14321 Lectorium {{---}} Лекция А.С. Станкевича] |
| − | * [https://en.wikipedia.org/wiki/Order-maintenance_problem Wikipedia {{---}} | + | * [https://en.wikipedia.org/wiki/Order-maintenance_problem Wikipedia {{---}} Order Maintance Problem] |
| − | |||
| − | |||
| + | [[Категория: Дискретная математика и алгоритмы]] | ||
| + | [[Категория: Алгоритмы и структуры данных]] | ||
[[Категория: Амортизационный анализ]] | [[Категория: Амортизационный анализ]] | ||
[[Категория: Структуры данных]] | [[Категория: Структуры данных]] | ||
Текущая версия на 19:15, 4 сентября 2022
List order maintance (рус. поддержание порядка в списке) — проблема поддержания списка со следующими операциями:
- — вставка нового элемента в список сразу после ;
- — удаление элемента из списка;
- — операция, возвращающая , если в списке находится до и иначе.
Существует реализация такой структуры, где выполняется за истинную , а операции добавления и удаления за амортизационную . Проблема поддержания порядка в списке возникает, к примеру, при реализации полностью персистентного дерева поиска.
Содержание
Алгоритм
Идея
Все операции, кроме , за может выполнить обычный двусвязный список, но с его помощью невозможно получить информацию о порядке объектов. Для реализации этой операции каждому узлу можно сопоставить некоторое число так, чтобы все числа строго возрастали от начала к концу списка. Таким образом, эти числа, которые в дальнейшим будут называться метками, задают порядок на элементах списка.
Ответить на запрос можно за , просто сравнив метки и . Добавление меток никак не влияет на реализацию операции . Однако реализацию потребуется изменить: при добавлении нового элемента после узла , узлу необходимо присвоить метку, которая строго больше предыдущего элемента и строго меньше следующего. В какой-то момент возникнет ситуация, что новой метки не найдётся, тогда метки можно перераспределить среди элементов списка так, чтобы для узла нашлась метка. Далее будет рассмотрен алгоритм, который позволяет эффективно реализовать эту идею.
Алгоритм за O(logn)
Способ хранения меток
Метки будут храниться в виде чисел в двоичной системе счисления. Требуется выбрать такую длину для меток, чтобы перераспределения не случались слишком часто. Если — длина каждой метки, то для начала пусть , где — количество элементов в списке. Если после добавления элементов какому-то элементу не хватит метки, увеличим на и пересчитаем все метки заново, распределив их равномерно. Заметим, что сразу после перераспределения меток, в среднем, между каждыми двумя элементами списка будет только одна свободная метка, так как при переходе к новому количество меток будет примерно в два раза больше количества элементов списка. Если же после удаления элемента из списка станет в раза больше , уменьшим на . Пересчет меток занимает амортизационно по аналогии с саморасширяющимся массивом. Однако очевидно, что в таком случае операция добавления за работать не будет, так как, если потребуется добавить между двумя элементами списка больше одного элемента, то новым элементам меток не хватит, и придется провести лишнее перераспределение меток, которое будет рассмотрено ниже. Позже, в доказательстве времени работы, значение будет несколько уточнено.
Все метки будут храниться в цифровом боре высоты (там представлены не только используемые метки, а вообще все возможные заданной длины). Введем некоторые обозначения:
- — количество помеченных (используемых) листьев (меток) в поддереве узла ;
- — количество всех листьев в поддереве ;
- — высота узла в цифровом боре.
Также в каждом узле дополнительно будет храниться:
- в листьях — используется ли уже эта метка;
- в нелистовых узлах — является ли узел переполненным.
Переполненным назовем узел, для которого для выбранного () выполнено . В листьях не хранится наличие переполненности, так как в листьях не может быть переполнения. В крайнем случае для листа: .
Перераспределение меток
Перераспределение меток потребуется выполнить в случае, когда для нового элемента не будет свободной метки. Пусть требуется выполнить операцию , но метка, следующая за меткой уже присвоена элементу . Тогда будем подниматься вверх от метки до тех пор, пока не будет найден первый непереполненный узел. Может случиться такое, что на всем пути до корня не встретится ни одного непереполненного узла. Чтобы этого избежать, уточним границы позже. Как только будет найден первый непереполненный узел, переназначим метки в поддереве этого узла так, чтобы они находились друг от друга на одинаковых расстояниях (места точно хватит, так как , если узел непереполненный). После этого между занятыми метками будет не меньше свободных меток.
Доказательство времени работы
Рассмотрим, как часто происходит перераспределение меток:
- Если в поддереве узла было проведено перераспределение меток, то повторное перераспределение меток в поддереве узла потребуется, когда сын этого узла снова переполнится. Если — сын , то он переполнится, когда . Чтобы это произошло, требуется, чтобы было сделано еще добавлений:
;
- С другой стороны, следующее перераспределение меток произойдет, когда станет больше
.
Получается, что за операций перераспределения меток требуется сделать операций добавления. Используя метод предоплаты, видим, что если за каждую операцию добавления брать монет, то за добавления накопится достаточное количество монет, чтобы расплатиться за следующую операцию перераспределения в узле .
Однако таким образом требуется платить за каждый уровень, а количество уровней (бит) равно . Тогда амортизированная стоимость добавления составляет .
Для того, чтобы на пути к корню точно встретился непереполненный узел, требуется уточнить границы : . Тогда операция добавления работает за .
Алгоритм за O(1)
Предыдущий алгоритм работает за логарифм из-за того, что слишком часто приходится перераспределять метки. Используем (модифицированный цифровой бор), чтобы улучшить время работы операции добавления до .
У каждого элемента списка будет две метки: глобальная и локальная. Глобальная задает блок, локальная — положение элемента внутри блока. Описание взаимодействия с метками:
- локальные метки внутри каждого блока каждому элементу от до будут жадно присвоены. Стоит заметить, что внутри блока никогда не будет проблемы, что кому-то не хватит метки или придется сделать перераспределение меток, так как, если каждый раз в качестве метки брать среднее значение, то для того, чтобы был конфликт из-за меток, нужно больше, чем ключей (противоречит условию);
- глобальные метки будут организованы в структуру, использовавшуюся в реализации операции за логарифмическое время. Глобальные метки для блоков придется менять, когда один из блоков переполнился. Тогда блок будет разделен на два, метка второму будет присвоена методом, описанным выше (поднимемся до первого непереполненного). Каждый блок будет иметь занятых меток. Аналогично, когда в каком-то блок становится слишком мало ключей, он будет слит с соседним.
Внутри блоков присваиваются ключи за , а аналогичный приведенному выше анализ показывает, что к перераспределению глобальных меток приводит изменений локальных меток. За эти изменения будет накоплено монет для изменения глобальных меток, тогда операция добавления работает за константное время.
Использование памяти
Выбор сильно влияет на реализацию структуры, так как зависит от выбранной . С увеличением , уменьшается стоимость операции добавления (количество монет, которые надо брать: ), но увеличивается , значит, требуется больше памяти, а, уменьшая , получаем выигрыш в памяти, но проигрыш во времени операции добавления. Так как для реализации структуры используется , требуется памяти.
Послесловие
Впервые реализацию такой структуры данных со всеми операциями за константное время амортизационно предложили[1] Dietz и Sleator, однако их доказательство времени работы было намного сложнее вышеизложенного анализа. Поэтому позже группа ученых во главе с Michael A. Bender разработала[2] более простое доказательство, изложенное выше, впервые описанное в их статье Two simlified algorithms for maintaining order in a list. Послесловие их статьи таково:
Dietz and Sleator is quite influential With its tags and its proofs by potential But to teach it in class Is a pain in the ass So our new result is preferential.