Изменения

|definition=[[Марковская цепь |Марковская цепь]] называется '''регулярной ''' (нормальнойангл. ''regular Markov chain''), если в матрице перехода P <tex>\forall i,j \ \ p_{ij} \neq 0</tex>она целиком состоит из одного [[Эргодическая марковская цепь#Циклический класс | циклического класса]].

{{ТеоремаВ регулярной Марковской цепи |statement=Цепь регулярна тогда и только тогда, когда существует такое <tex> n </tex>, что в матрице <tex> P^n </tex> все элементы ненулевые, то есть из любого состояния можно попасть перейти в любое другое за некоторое число ходов<tex> n </tex> переходов.}}

|statement=Пусть <tex>P_{[r\times r]}</tex> — {{---}} матрица перехода регулярной цепи, <tex>\varepsilon</tex> — {{---}} минимальный элемент этой матрицы. Пусть х — <tex>x</tex> {{---}} произвольный <tex>r</tex>-мерный вектор-столбец, имеющий максимальный элемент <tex>M_0</tex> и минимальный <tex>m_0</tex>. Пусть <tex>M_1</tex> и <tex>m_1</tex> {{--- }} максимальный и минимальный элементы <tex>Px</tex>. <br>

{{Теорема|statement=Регулярная марковская цепь [[Эргодическая марковская цепь|эргодична]]. Другими словами:<br>Пусть х' <tex>P</tex> {{- --}} регулярная переходная матрица. Тогда:<br><tex>\exists A: \displaystyle \lim_{n \to \infty}P^n = A</tex>;<br>каждая строка А представляет собой один и тот же вероятностный вектор <tex>\alpha = \{a_1, a_2, \ldots, a_r \}</tex>|proof=Рассмотрим вектор-столбец <tex>e_j</tex>, полученный из х заменой всех элементову которого <tex>j</tex>-й элемент равен <tex>1</tex>, кроме а все остальные равны <tex>0</tex>. Пусть <tex>M_n</tex> и <tex>m_0m_n</tex> на {{---}} минимальный и максимальный элементы столбца <tex>M_0P^n e_j</tex>. Тогда Так как <tex>P^n e_j = P \cdot P^{n-1} e_j</tex>, то из леммы следует, что <tex>x M_1 \leqslant x'geqslant M_2 \geqslant \ldots</tex>. Каждый элемент и <tex>Px'm_1 \leqslant m_2 \leqslant \ldots</tex> имеет види

<tex>am_0 + M_n - m_n \leqslant (1 - a2\varepsilon )M_0 = M_0 - a(M_0 M_{n- m_0)</tex>, где а 1} - элемент P, который домножается на <tex>m_0</tex>, причем <tex>a \geqslant \varepsilon</tex>. Поэтому наше выражение не превосходит <tex>M_0 m_{n- \varepsilon(M_0 - m_01})</tex>. Отсюда и из неравенства Пусть <tex>x \leqslant x'</tex> получается: <tex>M_1 \leqslant M_0 d_n = M_n - \varepsilon (M_0 - m_0)m_n</tex>., тогда

Применяя те же рассуждения для вектора -х, получим: <tex>-m_1 d_n \leqslant (1 -m_0 - 2 \varepsilon )^n d_0 = (1 -m_0 + M_02 \varepsilon)^n \to 0</tex>.

Складывая эти два неравенстваЗначит <tex>P^n e_j</tex> сходится к вектору, получаем все элементы которого равны между собой. Пусть <tex>M_1 a_j</tex> {{- m_1 --}} их общее значение. Тогда <tex>0 \leqslant a_j \leqslant M_0 1</tex>. Заметим, что <tex>P^n e_j</tex> {{-- m_0 - 2\varepsilon (M_0 }} <tex>j</tex>- m_0) тый столбец матрицы <tex>P^n</tex>. Рассмотрим все <tex>e_j</tex> для <tex>j = (1 - , 2, \varepsilon )(M_0 - m_0)ldots</tex>. Тогда <tex>P^n</tex> сходится к матрице <tex>A</tex>, чу которой по строкам стоит один и тот же вектор <tex>\alpha = \{a_1, a_2, \ldots, a_r \}</tex>.тТак как в каждой матрице <tex>P^n</tex> сумма элементов в строке равна <tex>1</tex>, то то же самое справедливо и для предельной матрицы <tex>A</tex>.дТеорема доказана.}}

{{Определение|definition=Матрица <tex>A</tex> называется '''предельной матрицей''' (англ. ''limiting matrix''), вектор <tex>\alpha</tex> {{---}} '''предельным распределением''' (англ. ''limiting distribution'').}} = Основная теорема регулярных цепей = Следствия ==

|statement=Пусть Р <tex>P, A, \alpha</tex> {{--- регулярная переходная матрица}} объекты из предыдущей теоремы. Тогдасправедливы факты:<br>* для любого вероятностного вектора <tex>\exists A: pi \ \ \ \displaystyle \lim_{n \to \infty}\pi P^n = \alpha</tex>* <tex>\alpha</tex> {{---}} единственный вектор, для которого <tex>\alpha P = \alpha</tex>* <tex>AP = PA = A</tex>|proof=Пусть <brtex>\xi</tex>;{{---}} вектор-столбец, состоящий из единиц. каждая строка А представляет собой один и тот же * <tex>\pi</tex> {{---}} вероятностный вектор , значит <tex>\pi \xi = 1 </tex> ( сумма его элементов равна <tex>1</tex> ), значит <tex>\pi A = \pi \xi \alpha = \alpha</tex>. Но <tex>\displaystyle \lim_{n \to \infty} \pi P^n = \pi A = \alpha</tex> {{---}} первый пункт доказан.* Пусть <tex>\beta : \ \ \beta P = \beta</tex>. Тогда <tex>\forall n \ \beta P^n = \beta \Rightarrow \beta = \beta A = \alpha </tex>. Второй пункт доказан.* <tex>\displaystyle \lim_{n \to \infty} P^n = A \Leftrightarrow P \cdot \lim_{n \to \infty} P^n = A \Leftrightarrow \lim_{a_1, a_2, n \ldots, a_n to \infty}P^n \cdot P = A</tex>. Третий пункт доказан.

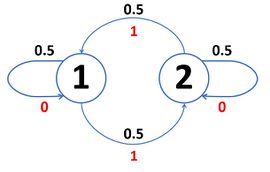
ДоказательствоТаким образом у регулярных цепей есть свойство:через достаточно большое количество ходов будет существовать постоянная вероятность нахождения цепи в состоянии <tex>s_i</tex>, и эта вероятность не зависит от начального распределения, а зависит только от матрицы <tex>P</tex>. == Примеры ==[[File:Пример регулярной цепи.jpg|thumb|270px|Пример регулярной цепи (черным цветом обозначена вероятность, красным - выпавшая сторона монеты)]]Самый очевидный и тривиальный пример регулярной цепи: Пусть у нас есть два состояния {{---}} <tex>1</tex> и <tex>2</tex>. Каждый ход мы кидаем честную монету {{---}} если выпал <tex>0</tex>, то цепь остается в предыдущем состоянии, если <tex>1</tex> {{---}} цепь меняет свое состояние.

<tex>M_n - m_n P = \begin{bmatrix}0.5 & 0.5 \\0.5 & 0.5 \end{bmatrix}</tex> Тогда <tex>\forall n \ \ P^n = P = A,\ \alpha = \{ 0.5, 0.5 \} ,\leqslant (,</tex>то есть через достаточно большое количество ходов наша система будет ''равновероятно'' находится как в состоянии <tex>1 </tex>, так и в состоянии <tex>2</tex>, независимо от начального распределения. Более интересный пример {{---}} если мы будем управлять переходом состояний с помощью нечестной монеты. Пусть <tex>a</tex> {{-- 2-}} вероятность выпадения <tex>0</tex> на монете.  Матрица переходов будет выглядеть так: <tex>P = \varepsilon )(M_begin{nbmatrix}a & 1 -a \\1} - m_a & a \end{bmatrix}</tex> Тогда при возведении <tex>P</tex> в степень <tex>n-</tex> элементы будут стремится к <tex>\dfrac{1}){2}</tex>с разных сторон. Пусть То есть вектор <tex>d_n \alpha = M_n - m_n\{ 0.5, 0.5 \}</tex>, тогдатаким образом от честности монеты ничего не зависит.

<tex>d_n \leqslant (1 - 2 \varepsilon )^n d_0 = (1 - 2 \varepsilon)^n \to 0</tex>= См.также ==*[[Марковская цепь]]*[[Эргодическая марковская цепь]]

Значит <tex>P^n \rho _j</tex> сходится к вектору, все элементы которого равны между собой== Источники информации ==*''Дж. Пусть <tex>a_j</tex> - их общее значение. Тогда <tex>0 \leqslant a_j \leqslant 1</tex>. ЗаметимКемени, что <tex>P^n \rho _j</tex> - j-тый столбец матрицы <tex>P^n</tex>Дж. Рассмотрим все <tex>\rho _j</tex> для <tex>j = 1Снелл'' Конечные цепи Маркова, 2, \ldots</tex>. Тогда <tex>P^n</tex> сходится к матрице А, у которой по строкам стоит один и тот же вектор <tex>\alpha = \{a_1, a_2, \ldots, a_n \}</tex>.стр 93Так как в каждой матрице <tex>P^n</tex> сумма элементов в строке равна 1, то то же самое справедливо [[Категория:Дискретная математика и для предельной матрицы А. Теорема доказана.алгоритмы]]

== Литература ==Дж. Кемени, Дж. Снелл "Конечные [[Категория: Марковские цепи Маркова", стр 93]]