1632
правки
Изменения
м
{{В разработке}}
rollbackEdits.php mass rollback
= Линейные программы =
Определения и основные понятия, связанные с булевыми функциями описаны в статье [[Определение булевой функции|"определение булевой функции"]].<br>
{{Определение
|definition='''Линейная программа''' {{---}} последовательность строк вида <tex>x {\{s_i\}}_{i=n}^t</tex>, в которой <tex>s_i</tex> имеет вид <tex>x_i = F(x_1x_{a_1}, x_2x_{a_2}, \dots ldots , x_nx_{a_m})</tex>, где <tex>xx_i, x_1x_{a_1}, \dots , x_nx_{a_m}</tex> {{---}} переменные, каждое из чисел <tex>a_j</tex> меньше <tex>i</tex>, а <tex>F</tex> {{---}} <tex>km</tex>-местная базисная функция. Такая линейная программа имеет <tex>n</tex> входных переменных, которые не выражаются через операции вычисления.
}}
'''Пример'''<br>
Для базиса <tex>B_0 = \{\vee, \wedge, \neg \}</tex> линейная программа состоит из присваиваний видаможет выглядеть следующим образом: * <tex>A A_2 = B A_0 \wedge CA_1</tex>;* <tex>E A_2 = A A_0 \vee BA_1</tex>;* <tex>D A_1 = \neg EA_0</tex>.
<br>
Линейная программа <tex>P</tex> с выделенными переменными <tex>x_1,\dots , x_n</tex> порождает для каждого набора <tex>\sigma_1, \dots , \sigma_n</tex> значений входных переменных естественный процесс вычисления:
# Переменным <tex>x_1, \dots , x_n</tex> присваиваются значения <tex>\sigma_1, \dots , \sigma_n</tex>, соответственно, а каждой из остальных переменных присваивается значение <tex>0</tex>;
# Последовательно выполняются присваивания программы <tex>P</tex>, в результате чего каждая из переменных <tex>x_i \; \forall i = 1 .. n</tex> программы получит итоговое значение <tex>P_ZP_i(\sigma_1, \dots , \sigma_n)</tex>.
{{Определение
|definition='''Программа''' <tex>P</tex> со входными переменными <tex>x_1,\dots , x_n</tex> '''вычисляет''' в выходной переменной <tex>Zx_m</tex> '''функцию''' <tex>F(x_1, \dots , x_n)</tex>, если для любого набора значений входов <tex>\sigma_1, \dots , \sigma_n</tex> после завершения работы <tex>P_ZP_m(\sigma_1, \dots , \sigma_n) = F(\sigma_1, \dots , \sigma_n)</tex>.
}}
|statement=
<br>
# По каждой логической схеме <tex>S</tex> со входами <tex>x_1, \dots , x_n</tex> и функциональными элементами <tex>v_1, \dots , v_m</tex> можно эффективно построить линейную программу <tex>P_S</tex> со входными переменными <tex>x_1, \dots , x_n</tex> и рабочими переменными <tex>v_1x_{n + 1}, \dots , v_mx_{n + m}</tex>, которая в любой переменной <tex>v_ix_i, i = \in [1, \dots + n, m + n]</tex>, вычисляет функцию <tex>f_{v_ix_i}(x_1, \ldots , x_n)</tex>;<br><br># По каждой линейной программе <tex>P</tex> со входными переменными <tex>x_1, \dots , x_n</tex>, вычисляющей в выходной переменной <tex>Zx_m</tex> некоторую функцию <tex>F(x_1, \dots , x_n)</tex> можно эффективно построить логическую схему <tex>S_P</tex> со входами <tex>x_1,\dots , x_n</tex>, в которой имеется вершина <tex>v</tex> такая, что <tex>f_v(x_1, \dots , x_n) = F(x_1, \dots , x_n)</tex>.
|proof=
'''(1)'''<br>
Пусть <tex>S</tex> {{---}} схема со входами <tex>x_1, \dots , x_n</tex> и функциональными элементами <tex>v_1, \dots , v_m</tex>. Построим по ней линейную программу <tex>P_S</tex> со входными переменными <tex>x_1, \dots , x_n</tex> следующим образом. [[Использование обхода в глубину для топологической сортировки | Топологически отсортируем]] все входные и функциональные вершины <tex>S</tex>: <tex>u_1, \dots , u_{n + m}</tex>. Программа <tex>P_S</tex> будет последовательностью <tex>m</tex> присваиваний.<br>
* Пусть вершина <tex>u_{i + n + i}</tex> помечена <tex>\neg</tex>, и в нее входит ребро из <tex>u_j</tex>. Тогда в качестве <tex>i</tex>-ой команды поместим в <tex>P_S</tex> присваивание <tex>u_x_{i + n + i}= \neg u_jx_j</tex>;* Пусть вершина <tex>u_{i + n + i}</tex> помечена <tex>\circ \in \{ \wedge , \vee \}</tex>, и в нее входят ребра из <tex>u_j</tex> и <tex>u_k</tex>. Тогда в качестве <tex>i</tex>-ой команды поместим в <tex>P_S</tex> присваивание <tex>u_x_{i + n + i} = u_j x_j \circ u_kx_k</tex>.
<br>
Топологическая сортировка вершин гарантирует, что <tex>j < n + i \wedge k < n + i</tex>. Поэтому при вычислении <tex>u_x_{n + i}</tex> значения аргументов уже получены и индукцией по глубине легко показать, что для любого <tex>i \forall i = in [1, \dots , m]</tex> программа <tex>P_S</tex> вычисляет в переменной <tex>v_ix_i</tex> функцию <tex>f_{v_ix_i}(x_1, \dots, x_n)</tex>.
}}
'''Пример'''
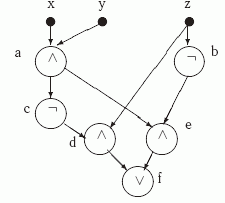
[[Файл:Logic_scheme_sample_boolean_functions_and_linear_programs.gif|300px|thumb|centerleft|Пример схемы]]
Воспользуемся только что доказанной теоремой, и построим на основании этой схемы линейную программу.<br>
Установим соответствие между вершинами схемы и переменными: <tex>x \; — \; x_0, \; y \; — \; x_1, \; z \; — \; x_2, \; a \; — \; x_3, \; b \; — \; x_4, \; c \; — \; x_5, \; d \; — \; x_6, \; e \; — \; x_7, \; f \; — \; x_8</tex>.<br>
Результатом топологической сортировки данного графа может стать последовательность вершин: <tex>x, y, z, a, b, c, d, e, f</tex>. Тогда программа <tex>P_S</tex> будет иметь следующий вид:<br>
<tex>a x_3 = x x_0 \wedge yx_1</tex><br><tex>b x_4 = \neg zx_2</tex><br><tex>c x_5 = \neg ax_3</tex><br><tex>d x_6 = c x_5 \wedge zx_2</tex><br><tex>e x_7 = a x_3 \wedge bx_4</tex><br><tex>f x_8 = d x_6 \vee ex_7</tex><br>
<br>
{{Утверждение
