Изменения

а плоскость <math>P_2</math> не является(отсутствует нейтральный элемент относительно сложения).

Алиса будет получать получать

==ОпределенияВекторные пространства и определители==Вспомним несколько фактов из линейной алгебры.{{Определение|definition=Набор векторов <math>\{\vec{e}_i\}_{i=1}^n</math> называется '''линейно независимым''' (ЛНЗ), если его линейная комбинация <math>\sum_{i=1}^n \alpha_i \vec{e}_i</math> равна нулю только в том случае, если она тривиальная, то есть <math>\forall i : \alpha_i = 0</math>.}}{{Определение|definition=Векторное пространство называется <math>d</math>-мерным, если в нём существует набор из <math>d</math> линейно независимых векторов,и не существует набора из <math>d + 1</math> линейно независимого вектора.}}===Единственность разложения в базис=== {{Утверждение|id=vectorUniqueness|statement=В <math>d</math>-мерном пространстве любой вектор <math>\vec{A}</math> единственным образом раскладывается в базисе из <math>d</math> линейно независимых векторов <math>\{\vec{e}_i\}_{i=1}^d</math> как <math>\sum_{i=1}^d\alpha_i\vec{e}_i</math>.|proof=Если мы добавим в базис вектор <math>\vec{A}</math>, то он обязательно станет линейно зависимым, и, значит, найдутся такие <math>\beta</math> и <math>\{\alpha_i\}</math>, что <math>\displaystyle \beta \vec{A} + \sum_{i=1}^d\alpha_i\vec{e}_i=0 \implies\vec{A} = \sum\limits_{i=1}^d-\frac{\alpha_i}{\beta}\vec{e}_i</math>, и, значит, разложение существует. Теперь пусть есть два разложения <math>\sum_{i=1}^d\alpha_i\vec{e}_i=\vec{A}</math> и <math>\sum_{i=1}^d\beta_i\vec{e}_i=\vec{A}</math>.Тогда <math>\displaystyle \vec{A} - \vec{A} = \vec{0} = \sum_{i=1}^d(\alpha_i - \beta_i)\vec{e}_i</math>, однако такое может быть только в том случае, если линейная комбинация тривиальная, то есть<math>\alpha_i - \beta_i = 0 \implies \alpha_i = \beta_i \implies</math> &nbsp; разложение единственно.}} ===Матрица перехода=== Мы можем переходить из одного базиса в другой.Пусть у нас есть базисы <math>\{\vec{e}_i\}_{i=1}^d</math> и <math>\{\vec{f}_i\}_{i=1}^d</math>. <math>\displaystyle\vec{A} = \sum_{i=1}^d\alpha_i\vec{e}_i = \sum_{i=1}^d\beta_i\vec{f}_i \\\vec{e}_i = \sum_{j=1}^d c_{ij}\vec{f}_j \\\vec{A} = \sum_{i=1}^d\alpha_i\vec{e}_i =\sum_{i=1}^d \alpha_i \sum_{j=1}^d c_{ij} \vec{f}_j =\sum_{j=1}^d \vec{f}_j \sum_{i=1}^d \alpha_i c_{ij} \\\beta_j = \sum_{i=1}^d\alpha_i c_{ij} \implies\begin{pmatrix} \beta_1 \\ \beta_2 \\ \vdots \\ \beta_d \end{pmatrix} =\begin{pmatrix}c_{11} & c_{21} & \cdots & c_{d1} \\c_{12} & c_{22} & \cdots & c_{d2} \\\vdots & \vdots & \ddots & \vdots \\c_{1d} & c_{2d} & \cdots & c_{dd}\end{pmatrix}\cdot\begin{pmatrix} \alpha_1 \\ \alpha_2 \\ \vdots \\ \alpha_d \end{pmatrix}</math> ===Определитель=== Следующий факт позволяет красиво записывать один подозрительно часто появляющийся определитель. <math> \displaystyle\begin{vmatrix}a_1 - p \\ a_2 - p \\ \vdots \\ a_n - p\end{vmatrix}= \begin{vmatrix}a_1 - p & 0 \\ a_2 - p & 0 \\ \vdots & \vdots \\ a_n - p & 0 \\ p & 1\end{vmatrix}= \begin{vmatrix}a_1 & 1 \\ a_2 & 1 \\ \vdots & \vdots \\ a_n & 1 \\ p & 1\end{vmatrix}</math> ==Аффинные пространства==

|definition='''Аффинное пространство''' – — это либо вырожденное пустое множество, либо кортеж <math>\langle A, V, (+)\rangle</math>, состоящий из непустого множества точек <math>A</math>, векторного пространства <math>V</math> и действия <math>(+) : A \times V \rightarrow A</math>, удовлетворяющего следующим свойствам:

|definition=Если <math>\langle A, V, (+)\rangle</math> – — это аффинное пространство, то <math>B \subset A</math> является '''аффинным подпространством''' пространства <math>\langle A, V, (+)\rangle</math>, если любая аффинная комбинация любого множества точек из <math>B</math> принадлежит <math>B</math>.

|statement=Пусть <math>\langle A, V, (+)\rangle</math> – — это аффинное пространство.

|statement=Пусть <math>\langle A, V, (+)\rangle</math> – — это аффинное пространство. Пусть <math>\{a_i\}_{i \in I}</math> – — множество точек из <math>A</math>. Если для какого-то <math>i \in I</math> множество векторов <math>\{\overrightarrow{a_i a_j}\}_{j \in I \setminus \{i\}}</math> линейно независимо, то для любого <math>i \in I</math> множество <math>\{\overrightarrow{a_i a_j}\}_{j \in I \setminus \{i\}}</math> будет линейно независимо.|proof=Пусть для какого-то <math>i \in I</math> множество векторов <math>\{\overrightarrow{a_i a_j}\}_{j \in I \setminus \{i\}}</math> линейно независимо, <math>k \in I</math> и пусть есть такой набор <math>\{\lambda_j\}_{j \in I \setminus \{k\}}</math>, что <math>\displaystyle \sum_{j \in I \setminus \{k\}} \lambda_j \cdot \overrightarrow{a_k a_j} = 0</math>. Поскольку <math>\overrightarrow{a_k a_j} = \overrightarrow{a_k a_i} + \overrightarrow{a_i a_j}</math>, мы имеем <math> \displaystyle \begin{aligned}\sum_{j \in I \setminus \{k\}} \lambda_j \cdot \overrightarrow{a_k a_j} &=\sum_{j \in I \setminus \{k\}} \lambda_j \cdot \overrightarrow{a_k a_i} + \sum_{j \in I \setminus \{k\}} \lambda_j \cdot \overrightarrow{a_i a_j} \\&= \sum_{j \in I \setminus \{k\}} \lambda_j \cdot \overrightarrow{a_k a_i} + \sum_{j \in I \setminus \{i,k\}} \lambda_j \cdot \overrightarrow{a_i a_j} \\&= \sum_{j \in I \setminus \{i,k\}} \lambda_j \cdot \overrightarrow{a_i a_j} - \left(\sum_{j \in I \setminus \{k\}} \lambda_j\right) \cdot \overrightarrow{a_i a_k} = 0 \text{.}\end{aligned}</math> Из этого следует, что <math>\forall j \in (I \setminus \{i, k\}) : \lambda_j = 0</math> и <math>\sum_{j \in I \setminus \{k\}} \lambda_j = 0</math>, поскольку набор векторов <math>\{\overrightarrow{a_i a_j}\}_{j \in I \setminus \{i\}}</math> линейно независим. Значит, <math>\forall j \in (I \setminus \{k\}) : \lambda_j = 0</math>, то есть линейная комбинация тривиальна.

|definition=Пусть <math>\langle A, V, (+)\rangle</math> – — это аффинное пространство. Множество точек <math>\{a_i\}_{i \in I}</math> '''аффинно независимо''', если для какого-то <math>i \in I</math> множество <math>\{\overrightarrow{a_i a_j}\}_{j \in I \setminus \{i\}}</math> линейно независимо.

==Базисы==<math>\displaystyle{{Определениеx|definition=Набор векторов <math>a_0 + \sum_{i=1}^n \vecalpha_i \cdot \overrightarrow{ea_0 a_i}_i= a_0 + \}_sum_{i=1}^n\beta_i \cdot \overrightarrow{a_0 a_i}</math> называется '''линейно независимым''' (ЛНЗ). Получаем, если его линейная комбинация что  <math>\displaystyle\sum_{i=1}^n \alpha_i \veccdot \overrightarrow{a_0 a_i}= \sum_{i=1}^n \beta_i \cdot \overrightarrow{ea_0 a_i}_i</math> равна нулю только в том случае. По [[#vectorUniqueness|лемме для векторного пространства]] такое разложение единственно, если она тривиальная, то есть <math>\forall i \in \left[1..n\right] : \alpha_i = 0\beta_i \implies \alpha_0 = \beta_0</math>. В обратную сторону доказывается идентично.

|definition=Векторное Пусть <math>\langle A, V, (+)\rangle</math> — это аффинное пространство называется . Множество точек <math>d\{a_i\}_{i \in I}</math>-мернымбудет называться '''аффинным базисом''' этого пространства, если в нём существует набор из множество векторов <math>d\{\overrightarrow{a_0 a_i}\}_{i=1}^n</math> линейно независимых векторов,и не существует набора из будет базисом <math>d + 1V</math> линейно независимого вектора. '''Барицентрическими координатами''' точки будут коэффициенты её аффинного разложения в этом базисе.

====Единственность==== {{Утверждение|statement=В <math>d</math>-мерном пространстве любой вектор Поскольку <math>\vec{forall x \in A}</math> единственным образом раскладывается в базисе из <math>d</math> линейно независимых векторов <math>\{\vec{e}_i\}_{i: x =1}^d</math> как <math>\sum_{i=1}^d\alpha_i\vec{e}_i</math>.|proof=Если мы добавим в базис вектор <math>a_0 + \vecoverrightarrow{Aa_0 x}</math>, то он обязательно станет линейно зависимым, и, значит, найдутся такие <math>\beta</math> и <math>\{\alpha_i\}</math>, что если множество <math>\displaystyle \beta \vec{A} + \sum_overrightarrow{i=1a_0 a_i}^d\alpha_i\vec{e}_i=0 \implies\vec{A} = \sum\limits__{i=1}^d-\frac{\alpha_i}{\beta}\vec{e}_in</math>ЛНЗ,то существует единственное разложение

и, значит, разложение существует<math> \displaystylex = a_0 + \sum_{i=1}^n \lambda_i \cdot \overrightarrow{a_0 a_i}</math>.

<math>\displaystyle x = \vec{A} left(1 - \vecsum_{A} i= \vec{0} = ^n \lambda_i \right) a_0 + \sum_{i=1}^d(n \alpha_i - \beta_i)\vec{e}_ilambda_i a_i</math>, однако такое может быть только в том случае, если линейная комбинация тривиальная, то есть<math>\alpha_i - \beta_i = 0 \implies \alpha_i = \beta_i \implies</math> &nbsp; разложение единственно.}} ====Матрица перехода====

Мы можем переходить из одного базиса значит, разложение в другой.Пусть у нас есть базисы <math>\{\vec{e}_i\}_{i=1}^d</math> аффинный базис всегда существует, и <math>\{\vec{f}_i\}_{i=1}^d</math>, по лемме, оно единственно. <math>\displaystyle\vec{A} = \sum_{i=1}^d\alpha_i\vec{e}_i = \sum_{i=1}^d\beta_i\vec{f}_i \ \land\ \vec{e}_i = \sum_{j=1}^d c_{ij}\vec{f}_j</math>

Также можно выделить <math>\displaystyle\vec{A} = \sum_{i=1}^d\alpha_i\vec{e}_i =\sum_{i=1}^d \alpha_i \sum_{j=1}^d c_{ij} \vec{f}_j =\sum_{j=1}^d \vec{f}_j \sum_{i=1}^d \alpha_i c_{ij}a_0</math>как начало координат, и представлять координаты так же, как это делается в векторном пространстве.Обычно так и делается.Осознание глубинного смысла сего действия остаётся читателям в качестве упражнения.

У нас есть гиперплоскость <tex>g</tex> и точки задающие её. В <tex>d</tex> мерном пространстве у нас будет <tex>d</tex> линейно аффинно независимых (ЛНЗ) точек <tex>a_1, a_2, \dots, a_d</tex>. Линейную независимость точек воспринимаем творчески. {{Определение |definition=Будем называть набор из <tex>d</tex> точек '''линейно независимым''', если мы можем выбрать одну из них, провести вектора от нее до всех остальных и получить <tex>d-1</tex> ЛНЗ вектор.}}

Возьмем в нашем пространстве еще одну выделенную точку <tex>p</tex>. Получившийся Если она не лежит в гиперплоскости, то получившийся набор <tex>a_1, a_2, \dots, a_d, p</tex> тоже будет ЛНЗаффинно независимым.

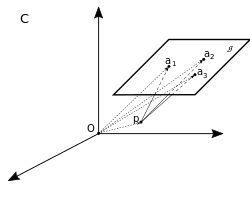
[[Файл:drawing-3.png|400px|thumb|right|Пример для <tex>\mathbb{R}^3</tex>]]Пусть у нас есть какая-то выделенная зарание заранее система координат <tex>C</tex>. Эта система приходит обычно вместе с какой-то задачей, и обычно она декартова. И у нас тоже будет сейчас декартова.

Мы знаем, что можно составить матрицу переходаиз начальной системы координат координат <tex>C</tex> в систему координат на векторах <math>\{\overrightarrow{p a_i}\}_{i=1}^d</math>, если умеем можно выразить координаты векторов эти вектора в исходной базовой системе координат <texmath>C</texmath>.А в нашем случае мы это сделать, конечно, можем: поскольку вектор существует между любыми парами точек, просто сопредставим сопоставим нашим точкам вектора, соединяющие начало координат <tex>O</tex> и очередную точку.

Запишем матрицу перехода и немножко преобразуем еёопределитель:[[Файл:drawing-3.png|400px|thumb|right|Пример для <tex>R^3</tex>]]

<tex>\det A ^ \mathrm{T}= \begin{pmatrixvmatrix} \overrightarrow{Oa_1} - \overrightarrow{Op} \\ \overrightarrow{Oa_2} - \overrightarrow{Op} \\ \vdots \\ \overrightarrow{Oa_d} - \overrightarrow{Op} \end{pmatrix}^ \mathrm{Tvmatrix} =\begin{pmatrixvmatrix} a_1 - p \\ a_2 - p\\ \vdots \\ a_d - p \end{pmatrixvmatrix}^ \mathrm{T} =\begin{pmatrixvmatrix} a_1 & 1 \\ a_2 & 1\\ \vdots & \vdots \\ a_d & 1 \\ p & 1 \end{pmatrix}^ \mathrm{Tvmatrix}</tex>.

В дальнейшем нас будут интересовать детерминант этой матрицы и его знак: <tex>\det(A) = \begin{vmatrix} a_1 & 1 \\ a_2 & 1\\ \vdots & \vdots \\ a_d & 1 \\ p & 1 \end{vmatrix}</tex>этого детерминанта.

|proof= По определению выпуклого множества. Возьмем две любые точки <tex>p_1</tex> и <tex>p_2</tex>, лежащие в одной области. По аксиоматике существует вектор <tex>\overrightarrow{p_1p_2}</tex> и по определению можно сделать линейную комбинацию. Значит можем получить любую точку между <tex>p_1</tex> и <tex>p_2</tex>, лежащую с ними на одной прямой, отложив от <tex>p_1</tex> вектор <tex>\alpha \cdot \overrightarrow{p_1p_2}</tex>, где <tex>\alpha \in [0..1]</tex>. Если подставить это в определитель, и вспомнить, что <math>1 = \alpha + (1 - \alpha)</math>, то получим <tex>\begin{vmatrix} a_1 & 1 \\ a_2 & 1\\ \vdots & \vdots \\ a_d & 1 \\ p_1 + \alpha \cdot \overrightarrow{p_1p_2} & 1 \end{vmatrix} = \begin{vmatrix} a_1 & 1 \\ a_2 & 1\\ \vdots & \vdots \\ a_d & 1 \\ \alpha p_2 + (1 - \alpha)p_1 & 1 \end{vmatrix} = \alpha \begin{vmatrix} a_1 & 1 \\ a_2 & 1\\ \vdots & \vdots \\ a_d & 1 \\ p_2 & 1 \end{vmatrix} +(1 - \alpha) \begin{vmatrix} a_1 & 1 \\ a_2 & 1\\ \vdots & \vdots \\ a_d & 1 \\ p_1 & 1 \end{vmatrix} </tex>.

Эта история о том, что даже когда мы притворяемся, что у нас нет метрики, мы неявно испоользуем топологию, индуцированную этой метрикой. Но, метрика, не единственна, и топология не единственна. Иногда нам достаточно топологии, которая даже может быть не индуцирована метрикой, или которая вообще не метризуема, но эта топология будет давать свойство непрерывности. Но тогда для нашей топогогии нужно будет доеказывать доказывать вышеупомянутый факт (про непрерывность кривой).