Контекстное моделирование — различия между версиями
SchrodZzz (обсуждение | вклад) (Новая страница: «{{Определение |definition= '''''Контекстное моделирование''''' — ''оценка вероятности появления с…») (Метки: правка с мобильного устройства, правка из мобильной версии) |
м (rollbackEdits.php mass rollback) |
||
| (не показано 15 промежуточных версий 2 участников) | |||
| Строка 1: | Строка 1: | ||
{{Определение | {{Определение | ||
|definition= | |definition= | ||
| − | '''''Контекстное моделирование''''' — ''оценка вероятности появления символа'' (элемента, пиксела, сэмпла и даже набора качественно разных объектов) в ''зависимости'' от непосредственно ему предыдущих, или контекста. | + | '''''Контекстное моделирование''''' (''context modeling'')— ''оценка вероятности появления символа'' (элемента, пиксела, сэмпла и даже набора качественно разных объектов) в ''зависимости'' от непосредственно ему предыдущих, или контекста. |
}} | }} | ||
{{Определение | {{Определение | ||
| Строка 8: | Строка 8: | ||
}} | }} | ||
===Оценка вероятности=== | ===Оценка вероятности=== | ||
| − | + | ''Контекстная модель'' строятся на основании ''обычных счетчиков частот'', связанных с текущим контекстом. Если мы обработали строку <tex>“кускувукус”</tex>, то для контекста <tex>“ку”</tex> счетчик символа «<tex>c</tex>» равен ''двум'', символ «<tex>в</tex>» — ''единице''. На основании этого статистики можно утверждать, что вероятность появления «<tex>c</tex>» после <tex>“ку”</tex> равна <tex> \dfrac{2}{3}</tex> , а вероятность появления «<tex>в</tex>» равна <tex> \dfrac{1}{3}</tex>, т.е. Оценки формируются на основе уже просмотренной части потока. | |
{{Определение | {{Определение | ||
|definition= | |definition= | ||
| − | '''''Порядок контекстной модели''''' — длина соответствующего этой модели контекста . Если порядок <tex>КМ</tex> равен <tex>o</tex>, то будем обозначать такую <tex>КМ</tex> как <tex>“КМ(o)”</tex> | + | '''''Порядок контекстной модели''''' (''order context model'') — длина соответствующего этой модели контекста . Если порядок <tex>КМ</tex> равен <tex>o</tex>, то будем обозначать такую <tex>КМ</tex> как <tex>“КМ(o)”</tex>. |
}} | }} | ||
| − | ===Пример=== | + | {{Определение |
| + | |definition= | ||
| + | '''''Модель с полным смешиванием''''' (''fully blended model'') — модель, в которой предсказание определяется статистикой <tex>KM</tex> всех используемых порядков. | ||
| + | }} | ||
| + | ====Вычисление смешанной вероятности==== | ||
| + | Введем следующие обозначения: | ||
| + | *<tex>p(s_i|o)</tex> — вероятность, присваемая в <tex>КМ(о)</tex> символу <tex>s_i</tex>. | ||
| + | *<tex>p(s_i)</tex> — смешанная вероятность. | ||
| + | *<tex>f(s_i|o)</tex> — частота появления <tex>s_i</tex> в соответствующем контексте порядка <tex>о</tex>. | ||
| + | *<tex>f(o)</tex> — общая частота появления соответствующего контекста порядка <tex>о</tex> в обработанной последовательности. | ||
| + | *<tex>\omega(o)</tex> — вес оценки <tex>КМ(о)</tex>. | ||
| + | |||
| + | Оценка <tex>p(s_i|o)</tex> обычно определяется через частоту символа <tex>s_i</tex> по тривиальной формуле: | ||
| + | |||
| + | <tex>p(s_i|o) = \dfrac{f(s_i|o)}{f(o)}</tex> | ||
| + | |||
| + | В общем случае смешанная вероятность <tex>p(s_i)</tex> выселяется так: | ||
| + | |||
| + | <tex>p(s_i) = \sum\limits_{о \in [-1, N]} \omega(o)\cdot p(s_i|o)</tex> | ||
| + | ====Пример==== | ||
Рассмотрим процесс оценки отмеченного на рисунке стрелочкой символа <tex>л</tex>, встречающегося в блоке <tex>“молочное</tex>'''''_'''''<tex>молоко”</tex> | Рассмотрим процесс оценки отмеченного на рисунке стрелочкой символа <tex>л</tex>, встречающегося в блоке <tex>“молочное</tex>'''''_'''''<tex>молоко”</tex> | ||
[[Файл: milk.png|350px|thumb|right|рис. 1]] | [[Файл: milk.png|350px|thumb|right|рис. 1]] | ||
| − | + | Будем использовать <tex>КМ(2)</tex> с полным смешиванием и использованием заданного набора фиксированных весов <tex>КМ</tex> разных порядков: <tex>\omega(2) = 0.6</tex>, <tex>\omega(1) = 0.3</tex> и <tex>\omega(0) = 0.1</tex>. Считаем, что в начале кодирования в <tex>КМ(o)</tex> создаются счетчики для всех символов алфавита <tex>\{“м”, “о”, “л”, “ч”, “н”, “е”,“\_”, “к”\}</tex> и инициализируются ''единицей''; счетчик символа после его обработки увеличивается на единицу. Для текущего символа «<tex>л</tex>» имеются контексты <tex>“мо”</tex>, <tex>“о”</tex> и <tex>“”</tex> (<tex>0</tex>-го порядка). К данному моменту для них накоплена статистика, показанная в ''таблице'' | |
{| style="background-color:#CCC;margin:0.5px" | {| style="background-color:#CCC;margin:0.5px" | ||
!style="background-color:#EEE"| Порядок | !style="background-color:#EEE"| Порядок | ||
!style="background-color:#EEE"| | !style="background-color:#EEE"| | ||
| − | !style="background-color:#EEE"| <tex> | + | !style="background-color:#EEE"| <tex>«м»</tex> |
| − | !style="background-color:#EEE"| <tex> | + | !style="background-color:#EEE"| <tex>«о»</tex> |
| − | !style="background-color:#EEE"| <tex> | + | !style="background-color:#EEE"| <tex>«л»</tex> |
| − | !style="background-color:#EEE"| <tex> | + | !style="background-color:#EEE"| <tex>«ч»</tex> |
| − | !style="background-color:#EEE"| <tex> | + | !style="background-color:#EEE"| <tex>«н»</tex> |
| − | !style="background-color:#EEE"| <tex> | + | !style="background-color:#EEE"| <tex>«е»</tex> |
| − | !style="background-color:#EEE"| <tex> | + | !style="background-color:#EEE"| <tex>«</tex>'''''_'''''<tex>»</tex> |
| − | !style="background-color:#EEE"| <tex> | + | !style="background-color:#EEE"| <tex>«к»</tex> |
|- | |- | ||
|style="background-color:#FFF;padding:2px 30px"| <tex>КМ(0)</tex> | |style="background-color:#FFF;padding:2px 30px"| <tex>КМ(0)</tex> | ||
| Строка 95: | Строка 114: | ||
|style="background-color:#FFF;padding:2px 30px"| <tex> — </tex> | |style="background-color:#FFF;padding:2px 30px"| <tex> — </tex> | ||
|} | |} | ||
| − | Оценка вероятности для символа <tex>л</tex> будет равна <tex> | + | Оценка вероятности для символа «<tex>л</tex>» будет равна <tex> p(л) = 0.1\cdot\dfrac{2}{19}+0.3\cdot\dfrac{1}{3}+0.6\cdot\dfrac{1}{1} = 0.71 </tex> |
| − | ==Метод | + | ====Метод неявного взвешивания==== |
| + | ''Метод неявного взвешивания'' связан с введением вспомогательного '''''символа ухода''''' (''escape''). ''Символ ухода'' не принадлежит к алфавиту сжимаемой последовательности. Фактически он используется для передачи ''декодеру'' указаний ''кодера''. Идея заключается в том, что если используемая <tex>КМ</tex> не позволяет оценить текущий символ (его счетчик равен нулю в этой <tex>КМ</tex>), то на выход посылается закодированный ''символ ухода'' и производится попытка ''оценить'' текущий символ в другой <tex>КМ</tex>, которой соответствует контекст иной длины. Обычно попытка оценки начинается с <tex>КМ</tex> наибольшего порядка <tex>N</tex>, затем в определенной последовательности осуществляется переход к контекстным моделям меньших порядков. | ||
| + | |||
| + | ==Алгоритм РРМ== | ||
===Описание=== | ===Описание=== | ||
| − | <tex>РРМ</tex> | + | {{Определение |
| + | |definition= | ||
| + | '''''Адаптивное моделирование''''' (''adaptive context modeling'') — метод моделирования, при котором, по мере кодирования модель изменяется по заданному алгоритму. | ||
| + | }} | ||
| + | {{Определение | ||
| + | |definition= | ||
| + | '''''Энтропийное кодирование''''' (''entropy coding'') — кодирование ''последовательности значений'' с возможностью ''однозначного'' восстановления с целью ''уменьшения'' объёма данных с помощью ''усреднения'' вероятностей появления элементов в ''закодированной'' последовательности. | ||
| + | }} | ||
| + | Обычно термин <tex>РРМ</tex> используется для обозначения контекстных методов в общем, по этой причине далее будет рассматриваться некий обобщенный алгоритм <tex>РРМ</tex>. | ||
| + | |||
| + | <tex>РРМ</tex> (''Prediction by partial matching'') — адаптивный алгоритм сжатия данных без потерь, основанный на контекстном моделировании и предсказании. Исходно кодеру и декодеру поставлена в соответствие ''начальная'' модель источника данных. Будем считать, что она состоит из <tex>КМ(-1)</tex>, присваивающей одинаковую вероятность всем символам алфавита входной последовательности. После обработки текущего символа кодер и декодер изменяют свои модели одинаковым образом, в частности ''наращивая'' величину оценки вероятности рассматриваемого символа. Следующий символ кодируется (декодируется) на основании новой, измененной модели, после чего модель снова модифицируется и т. д. На каждом шаге обеспечивается ''идентичность'' модели кодера и декодера за счет применения одинакового механизма ее обновления. | ||
| + | |||
| + | Если символ «<tex>s</tex>» обрабатывается при помощи <tex>РРМ</tex>, то, в первую очередь рассматривается <tex>KM(N)</tex>. Если она оценивает вероятность «<tex>s</tex>» числом, не равным нулю, то сама и используется для кодирования «<tex>s</tex>». Иначе выдается сигнал в виде символа ухода, и на основе меньшей по порядку <tex>KM(N-1)</tex> производится очередная попытка оценить вероятность «<tex>s</tex>». Кодирование происходит через уход к <tex>КМ</tex> меньших порядков до тех пор, пока «<tex>s</tex>» не будет оценен. <tex>КМ(-1)</tex> гарантирует, что это в конце концов произойдет. Таким образом, каждый символ кодируется серией кодов символа ухода, за которой следует код самого символа. Из этого следует, что вероятность ухода также можно рассматривать как вероятность перехода к контекстной модели меньшего порядка. | ||
| + | |||
| + | <tex> РРМ </tex> лишь ''предсказывает значение символа'', непосредственное сжатие осуществляется алгоритмами энтропийного кодирования, как например, алгоритм Хаффмана или арифметическое кодирование. | ||
| + | |||
===Пример=== | ===Пример=== | ||
| − | Имеется последовательность символов <tex>“абвавабввбббв”</tex> алфавита <tex> \{ | + | ====Кодирование==== |
| + | Имеется последовательность символов <tex>“абвавабввбббв”</tex> алфавита <tex> \{а, б, в, г\}</tex>, которая уже была ''закодирована''. | ||
[[Файл: Qq.png|350px|thumb|right|рис. 2]] | [[Файл: Qq.png|350px|thumb|right|рис. 2]] | ||
[[Файл: PpmPart.png|350px|thumb|right|рис. 3]] | [[Файл: PpmPart.png|350px|thumb|right|рис. 3]] | ||
| Строка 115: | Строка 153: | ||
!style="background-color:#EEE"| <tex>Бит</tex> | !style="background-color:#EEE"| <tex>Бит</tex> | ||
|- | |- | ||
| − | |style="background-color:#FFF;padding:2px 20px"| <tex>a</tex> | + | |style="background-color:#FFF;padding:2px 20px"| «<tex>a</tex>» |
|style="background-color:#FFF;padding:2px 20px"| <tex> — </tex> | |style="background-color:#FFF;padding:2px 20px"| <tex> — </tex> | ||
|style="background-color:#FFF;padding:2px 20px"| <tex>\dfrac{1}{2+1}</tex> | |style="background-color:#FFF;padding:2px 20px"| <tex>\dfrac{1}{2+1}</tex> | ||
| Строка 124: | Строка 162: | ||
|style="background-color:#FFF;padding:2px 20px"| <tex>1.6</tex> | |style="background-color:#FFF;padding:2px 20px"| <tex>1.6</tex> | ||
|- | |- | ||
| − | |style="background-color:#FFF;padding:2px 20px"| <tex>б</tex> | + | |style="background-color:#FFF;padding:2px 20px"| «<tex>б</tex>» |
|style="background-color:#FFF;padding:2px 20px"| <tex> — </tex> | |style="background-color:#FFF;padding:2px 20px"| <tex> — </tex> | ||
|style="background-color:#FFF;padding:2px 20px"| <tex>\dfrac{1}{2+1}</tex> | |style="background-color:#FFF;padding:2px 20px"| <tex>\dfrac{1}{2+1}</tex> | ||
| Строка 133: | Строка 171: | ||
|style="background-color:#FFF;padding:2px 20px"| <tex>2.6</tex> | |style="background-color:#FFF;padding:2px 20px"| <tex>2.6</tex> | ||
|- | |- | ||
| − | |style="background-color:#FFF;padding:2px 20px"| <tex>в</tex> | + | |style="background-color:#FFF;padding:2px 20px"| «<tex>в</tex>» |
|style="background-color:#FFF;padding:2px 20px"| <tex> — </tex> | |style="background-color:#FFF;padding:2px 20px"| <tex> — </tex> | ||
|style="background-color:#FFF;padding:2px 20px"| <tex>\dfrac{1}{2+1}</tex> | |style="background-color:#FFF;padding:2px 20px"| <tex>\dfrac{1}{2+1}</tex> | ||
| Строка 142: | Строка 180: | ||
|style="background-color:#FFF;padding:2px 20px"| <tex>1.6</tex> | |style="background-color:#FFF;padding:2px 20px"| <tex>1.6</tex> | ||
|- | |- | ||
| − | |style="background-color:#FFF;padding:2px 20px"| <tex>г</tex> | + | |style="background-color:#FFF;padding:2px 20px"| «<tex>г</tex>» |
|style="background-color:#FFF;padding:2px 20px"| <tex> — </tex> | |style="background-color:#FFF;padding:2px 20px"| <tex> — </tex> | ||
|style="background-color:#FFF;padding:2px 20px"| <tex>\dfrac{1}{2+1}</tex> | |style="background-color:#FFF;padding:2px 20px"| <tex>\dfrac{1}{2+1}</tex> | ||
| Строка 151: | Строка 189: | ||
|style="background-color:#FFF;padding:2px 20px"| <tex>2.6</tex> | |style="background-color:#FFF;padding:2px 20px"| <tex>2.6</tex> | ||
|} | |} | ||
| − | Пусть текущий символ равен <tex>г</tex>, т. е. <tex>?</tex> = <tex>г</tex>, тогда процесс его кодирования будет выглядеть следующим образом. | + | Пусть текущий символ равен «<tex>г</tex>», т. е. «<tex>?</tex>» = «<tex>г</tex>», тогда процесс его кодирования будет выглядеть следующим образом. |
| − | Сначала рассматривается контекст <tex>3</tex>-го порядка <tex>“ббв”</tex>. Ранее он не встречался, поэтому кодер, ничего не послав на выход, переходит к анализу статистики для контекста <tex>2</tex>-го порядка. В этом контексте (<tex>“бв”</tex>) встречались символ <tex>а</tex> и символ <tex>в</tex>, счетчики которых в соответствующей <tex>КМ</tex> равны <tex>1</tex> каждый, поэтому ''символ ухода'' кодируется с вероятностью <tex>\dfrac{1}{2+1}</tex>, где в знаменателе число <tex>2</tex> — наблюдавшаяся частота появления контекста <tex>“бв”</tex>, <tex>1</tex> — значение счетчика ''символа ухода''. В контексте <tex>1</tex>-го порядка <tex>в</tex> дважды встречался символ <tex>а</tex>, который исключается (маскируется), один раз также исключаемый <tex>в</tex> и один раз <tex>б</tex>, поэтому оценка вероятности ухода будет ''равна'' <tex>\dfrac{1}{1+1}</tex>. В <tex>КМ(0)</tex> символ <tex>г</tex> также оценить ''нельзя'', причем все имеющиеся в этой <tex>КМ</tex> символы <tex>а</tex>, <tex>б</tex>, <tex>в</tex> исключаются, так как уже встречались нам в <tex>КМ</tex> более высокого порядка. Поэтому вероятность ухода получается равной ''единице''. Цикл оценивания завершается на уровне <tex>КМ(-1)</tex>, где <tex>г</tex> к этому времени остается ''единственным'' до сих пор не попавшимся символом, поэтому он получает вероятность <tex>1</tex> и кодируется посредством <tex>0 | + | Сначала рассматривается контекст <tex>3</tex>-го порядка <tex>“ббв”</tex>. Ранее он не встречался, поэтому кодер, ничего не послав на выход, переходит к анализу статистики для контекста <tex>2</tex>-го порядка. В этом контексте (<tex>“бв”</tex>) встречались символ «<tex>а</tex>» и символ «<tex>в</tex>», счетчики которых в соответствующей <tex>КМ</tex> равны <tex>1</tex> каждый, поэтому ''символ ухода'' кодируется с вероятностью <tex>\dfrac{1}{2+1}</tex>, где в знаменателе число <tex>2</tex> — наблюдавшаяся частота появления контекста <tex>“бв”</tex>, <tex>1</tex> — значение счетчика ''символа ухода''. В контексте <tex>1</tex>-го порядка «<tex>в</tex>» дважды встречался символ «<tex>а</tex>», который исключается (маскируется), один раз также исключаемый «<tex>в</tex>» и один раз «<tex>б</tex>», поэтому оценка вероятности ухода будет ''равна'' <tex>\dfrac{1}{1+1}</tex>. В <tex>КМ(0)</tex> символ «<tex>г</tex>» также оценить ''нельзя'', причем все имеющиеся в этой <tex>КМ</tex> символы «<tex>а</tex>», «<tex>б</tex>», «<tex>в</tex>» исключаются, так как уже встречались нам в <tex>КМ</tex> более высокого порядка. Поэтому вероятность ухода получается равной ''единице''. Цикл оценивания завершается на уровне <tex>КМ(-1)</tex>, где «<tex>г</tex>» к этому времени остается ''единственным'' до сих пор не попавшимся символом, поэтому он получает вероятность <tex>1</tex> и кодируется посредством <tex>0</tex> бит. Таким образом, при использовании хорошего статистического кодировщика для представления «<tex>г</tex>» потребуется в целом примерно <tex>2.6</tex> бит. |
| − | Перед обработкой следующего символа создается <tex>КМ</tex> для строки <tex>“ббв”</tex> и производится модификация счетчиков символа <tex>г</tex> в созданной и во всех просмотренных <tex>КМ</tex>. В данном случае требуется изменение <tex>КМ</tex> всех порядков от <tex>0</tex> до <tex>N</tex>. | + | Перед обработкой следующего символа создается <tex>КМ</tex> для строки <tex>“ббв”</tex> и производится модификация счетчиков символа «<tex>г</tex>» в созданной и во всех просмотренных <tex>КМ</tex>. В данном случае требуется изменение <tex>КМ</tex> всех порядков от <tex>0</tex> до <tex>N</tex>. |
| + | ====Декодирование==== | ||
| + | Алгоритм декодирования ''абсолютно'' симметричен алгоритму кодирования. После декодирования символа в текущей <tex>КМ</tex> проверяется, не является ли он ''символом ухода''; если это так, то выполняется переход к <tex>КМ</tex> порядком ниже. Иначе считается, что исходный символ ''восстановлен'', он ''записывается'' в декодированный поток и осуществляется переход к следующему шагу. Содержание процедур обновления счетчиков, создания новых ''контекстных моделей'', прочих вспомогательных действий и последовательность их применения должны быть строго одинаковыми при кодировании и декодировании. Иначе возможна рассинхронизация копий модели кодера и декодера, что рано или поздно приведет к ошибочному декодированию какого-то символа. Начиная с этой позиции вся оставшаяся часть сжатой последовательности будет разжата неправильно. | ||
| + | Разница между кодами символов, оценки вероятности которых одинаковы, достигается за счет того, что <tex>РРМ</tex>-предсказатель передает кодировщику так называемые накопленные частоты (или накопленные вероятности) оцениваемого символа и его соседей или кодовые пространства символов. | ||
| + | Так, например, для контекста <tex>“бв”</tex> можно составить следующую таблицу: | ||
| + | {| style="background-color:#CCC;margin:0.5px; right" | ||
| + | !style="background-color:#EEE"| <tex>Символ</tex> | ||
| + | !style="background-color:#EEE"| <tex>Частота</tex> | ||
| + | !style="background-color:#EEE"| <tex>Оценка\ вероятности</tex> | ||
| + | !style="background-color:#EEE"| <tex>Накопительная\ оценка</tex> | ||
| + | !style="background-color:#EEE"| <tex>Кодовое\ пространство</tex> | ||
| + | |- | ||
| + | |style="background-color:#FFF;padding:2px 30px"| «<tex>а</tex>» | ||
| + | |style="background-color:#FFF;padding:2px 30px"| <tex> 0 </tex> | ||
| + | |style="background-color:#FFF;padding:2px 90px"| <tex> — </tex> | ||
| + | |style="background-color:#FFF;padding:2px 90px"| <tex> — </tex> | ||
| + | |style="background-color:#FFF;padding:2px 60px"| <tex> — </tex> | ||
| + | |- | ||
| + | |style="background-color:#FFF;padding:2px 30px"| «<tex>б</tex>» | ||
| + | |style="background-color:#FFF;padding:2px 30px"| <tex> 1 </tex> | ||
| + | |style="background-color:#FFF;padding:2px 90px"| <tex>\dfrac{1}{3}</tex> | ||
| + | |style="background-color:#FFF;padding:2px 90px"| <tex>\dfrac{1}{3}</tex> | ||
| + | |style="background-color:#FFF;padding:2px 60px"| <tex> [0\ldots0.33) </tex> | ||
| + | |- | ||
| + | |style="background-color:#FFF;padding:2px 30px"| «<tex>в</tex>» | ||
| + | |style="background-color:#FFF;padding:2px 30px"| <tex> 1 </tex> | ||
| + | |style="background-color:#FFF;padding:2px 90px"| <tex>\dfrac{1}{3}</tex> | ||
| + | |style="background-color:#FFF;padding:2px 90px"| <tex>\dfrac{2}{3}</tex> | ||
| + | |style="background-color:#FFF;padding:2px 60px"| <tex> [0.33\ldots0.66) </tex> | ||
| + | |- | ||
| + | |style="background-color:#FFF;padding:2px 30px"| «<tex>г</tex>» | ||
| + | |style="background-color:#FFF;padding:2px 30px"| <tex> 0 </tex> | ||
| + | |style="background-color:#FFF;padding:2px 90px"| <tex> — </tex> | ||
| + | |style="background-color:#FFF;padding:2px 90px"| <tex> — </tex> | ||
| + | |style="background-color:#FFF;padding:2px 60px"| <tex> — </tex> | ||
| + | |- | ||
| + | |style="background-color:#FFF;padding:2px 23px"| «<tex>esc</tex>» | ||
| + | |style="background-color:#FFF;padding:2px 30px"| <tex> 1 </tex> | ||
| + | |style="background-color:#FFF;padding:2px 90px"| <tex>\dfrac{1}{3}</tex> | ||
| + | |style="background-color:#FFF;padding:2px 95px"| <tex>1</tex> | ||
| + | |style="background-color:#FFF;padding:2px 60px"| <tex> [0.66\ldots1) </tex> | ||
| + | |} | ||
| + | Хороший кодировщик должен отобразить символ «<tex>s</tex>» с оценкой вероятности <tex>p(s)</tex> в код длины <tex>\log_2 p(s)</tex>, что и обеспечит сжатие всей обрабатываемой последовательности в целом. | ||
| + | |||
| + | ==Проблема нулевой частоты== | ||
| + | {{Определение | ||
| + | |definition= | ||
| + | '''''Проблема нулевой частоты''''' (''zero frequency problem'') — проблема обработки новых символов, ещё не встречавшихся во входном потоке. | ||
| + | }} | ||
| + | На сегодняшний день можно выделить ''два'' подхода к решению этой проблемы: ''априорные'' методы, основанные на предположениях о природе сжимаемых данных, и ''адаптивные методы'', которые пытаются приспособиться к сжимаемым данным. | ||
| + | ===Априорные методы=== | ||
| + | Выедем следующие обозначения: | ||
| + | *<tex>С</tex> — общее число просмотров контекста | ||
| + | *<tex>Q</tex> — количество разных символов в контексте | ||
| + | *<tex>Q_i</tex> — количество таких разных символов, что они встречались в контексте ровно <tex>i</tex> раз | ||
| + | *<tex>Esc_x</tex> — <tex>ОВУ</tex>(''оценка вероятности кода ухода'') по методу <tex>x</tex> | ||
| + | Изобретатели алгоритма <tex>РРМ</tex> предложили два метода <tex>ОВУ</tex>: так называемые метод <tex>A</tex> и метод <tex>B</tex>. Частные случаи алгоритма <tex>РРМ</tex> с использованием этих методов называются, соответственно, <tex> PPMA </tex> и <tex> PPMB </tex>. | ||
| + | |||
| + | <tex>PPMA:\ Esc_A = \dfrac{1}{С + 1}</tex> | ||
| + | |||
| + | <tex>PPMB:\ Esc_B = \dfrac{Q - Q_1}{С}</tex> | ||
| + | |||
| + | Затем был разработан метод <tex>С</tex>, а в след за ним метод <tex>D</tex>: | ||
| + | |||
| + | <tex>PPMC:\ Esc_C = \dfrac{Q}{С + Q}</tex> | ||
| + | |||
| + | <tex>PPMD:\ Esc_D = \dfrac{Q}{2\cdotС}</tex> | ||
| + | |||
| + | ===Адаптивные методы=== | ||
| + | {{Определение | ||
| + | |definition= | ||
| + | '''''SEE''''' (''Secondary Escape Estimation'') — модель оценки, которая ''адаптируется'' к обрабатываемым данным. | ||
| + | }} | ||
| + | Для нахождения <tex>ОВУ</tex> строятся <tex>контексты\ ухода</tex> (''Escape Context''), формируемые из различный полей. Всего используется <tex>4</tex> поля, в которых содержится информация о: | ||
| + | *порядке <tex>РРМ-</tex>контекста | ||
| + | *количестве уходов | ||
| + | *количестве успешных кодирований | ||
| + | *последних двух символах <tex>РРМ-</tex>контекста | ||
| + | |||
| + | <tex>ОВУ</tex> для текущего контекста находится путем взвешивания оценок, которые дают три контекста ухода (<tex>order-2\ EC</tex>, <tex>order-1\ EC</tex>, <tex>order-0\ EC</tex>), соответствующие текущему <tex>РРМ-</tex>контексту. <tex>Order-2\ EC</tex> наиболее точно соответствует ''текущему'' контексту, контексты ''ухода'' порядком ниже формируются путем выбрасывания части информации полей <tex>order-2\ EC</tex>. При взвешивании контекстов ухода используются следующие веса <tex>w</tex>: | ||
| + | |||
| + | <tex>\dfrac{1}{w} = p \cdot log_2 \dfrac{1}{p} + (1 - p) \cdot log_2 \dfrac{1}{1 - p}</tex>, где <tex>p - ОВУ</tex>, которую дает данный взвешиваемый контекст. | ||
| + | |||
| + | Величину, которая формируется из фактического количества успешных кодирований и количества уходов в <tex>PPM</tex>-контекстах, соответствующих этому <tex>EC</tex> обозначим как '''''<tex>p_i</tex>'''''. | ||
| + | |||
| + | <tex>PPMZ:\ Esc_z = \dfrac{\sum\limits_{i \in [0, 2]} w_{i}\cdot p_{i}}{\sum\limits_{i \in [0, 2]} w_{i}}</tex> | ||
| + | |||
| + | ==См. также== | ||
| + | *[[Алгоритм LZMA]] | ||
| + | *[[Алгоритм Хаффмана]] | ||
| + | *[[Арифметическое кодирование]] | ||
| + | |||
| + | ==Источники информации== | ||
| + | *[ftp://ftp.cs.brown.edu/pub/techreports/93/cs93-28.pdf The design and analysis of efficient lossless data compression systems] | ||
| + | *[http://rahilshaikh.weebly.com/uploads/1/1/6/3/11635894/data_compression.pdf Introduction to Data Compression] | ||
| + | *[https://en.wikipedia.org/wiki/Prediction_by_partial_matching Prediction by partial matching] | ||
| + | *[http://ctxmodel.net/files/PPMd/ShkarinPPMII.pdf PPM one step to practicality] | ||
| + | *[http://www.compression.ru/book/pdf/compression_methods_part1_2-4.pdf Методы сжатия данных] | ||
| + | |||
| + | [[Категория: Дискретная математика и алгоритмы]] | ||
| + | [[Категория: Алгоритмы сжатия]] | ||
Текущая версия на 19:19, 4 сентября 2022
| Определение: |
| Контекстное моделирование (context modeling)— оценка вероятности появления символа (элемента, пиксела, сэмпла и даже набора качественно разных объектов) в зависимости от непосредственно ему предыдущих, или контекста. |
| Определение: |
| Если длина контекста ограничена, то такой подход будем называть контекстным моделированием ограниченного порядка (finite-context modeling), при этом под порядком понимается максимальная длина используемых контекстов . |
Содержание
Оценка вероятности
Контекстная модель строятся на основании обычных счетчиков частот, связанных с текущим контекстом. Если мы обработали строку , то для контекста счетчик символа «» равен двум, символ «» — единице. На основании этого статистики можно утверждать, что вероятность появления «» после равна , а вероятность появления «» равна , т.е. Оценки формируются на основе уже просмотренной части потока.
| Определение: |
| Порядок контекстной модели (order context model) — длина соответствующего этой модели контекста . Если порядок равен , то будем обозначать такую как . |
| Определение: |
| Модель с полным смешиванием (fully blended model) — модель, в которой предсказание определяется статистикой всех используемых порядков. |
Вычисление смешанной вероятности
Введем следующие обозначения:
- — вероятность, присваемая в символу .
- — смешанная вероятность.
- — частота появления в соответствующем контексте порядка .
- — общая частота появления соответствующего контекста порядка в обработанной последовательности.
- — вес оценки .
Оценка обычно определяется через частоту символа по тривиальной формуле:
В общем случае смешанная вероятность выселяется так:
Пример
Рассмотрим процесс оценки отмеченного на рисунке стрелочкой символа , встречающегося в блоке _
Будем использовать с полным смешиванием и использованием заданного набора фиксированных весов разных порядков: , и . Считаем, что в начале кодирования в создаются счетчики для всех символов алфавита и инициализируются единицей; счетчик символа после его обработки увеличивается на единицу. Для текущего символа «» имеются контексты , и (-го порядка). К данному моменту для них накоплена статистика, показанная в таблице
| Порядок | _ | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Частоты | |||||||||
| Накопленные Частоты | |||||||||
| Частоты | |||||||||
| Накопленные Частоты | |||||||||
| Частоты | |||||||||
| Накопленные Частоты |
Оценка вероятности для символа «» будет равна
Метод неявного взвешивания
Метод неявного взвешивания связан с введением вспомогательного символа ухода (escape). Символ ухода не принадлежит к алфавиту сжимаемой последовательности. Фактически он используется для передачи декодеру указаний кодера. Идея заключается в том, что если используемая не позволяет оценить текущий символ (его счетчик равен нулю в этой ), то на выход посылается закодированный символ ухода и производится попытка оценить текущий символ в другой , которой соответствует контекст иной длины. Обычно попытка оценки начинается с наибольшего порядка , затем в определенной последовательности осуществляется переход к контекстным моделям меньших порядков.
Алгоритм РРМ
Описание
| Определение: |
| Адаптивное моделирование (adaptive context modeling) — метод моделирования, при котором, по мере кодирования модель изменяется по заданному алгоритму. |
| Определение: |
| Энтропийное кодирование (entropy coding) — кодирование последовательности значений с возможностью однозначного восстановления с целью уменьшения объёма данных с помощью усреднения вероятностей появления элементов в закодированной последовательности. |
Обычно термин используется для обозначения контекстных методов в общем, по этой причине далее будет рассматриваться некий обобщенный алгоритм .
(Prediction by partial matching) — адаптивный алгоритм сжатия данных без потерь, основанный на контекстном моделировании и предсказании. Исходно кодеру и декодеру поставлена в соответствие начальная модель источника данных. Будем считать, что она состоит из , присваивающей одинаковую вероятность всем символам алфавита входной последовательности. После обработки текущего символа кодер и декодер изменяют свои модели одинаковым образом, в частности наращивая величину оценки вероятности рассматриваемого символа. Следующий символ кодируется (декодируется) на основании новой, измененной модели, после чего модель снова модифицируется и т. д. На каждом шаге обеспечивается идентичность модели кодера и декодера за счет применения одинакового механизма ее обновления.
Если символ «» обрабатывается при помощи , то, в первую очередь рассматривается . Если она оценивает вероятность «» числом, не равным нулю, то сама и используется для кодирования «». Иначе выдается сигнал в виде символа ухода, и на основе меньшей по порядку производится очередная попытка оценить вероятность «». Кодирование происходит через уход к меньших порядков до тех пор, пока «» не будет оценен. гарантирует, что это в конце концов произойдет. Таким образом, каждый символ кодируется серией кодов символа ухода, за которой следует код самого символа. Из этого следует, что вероятность ухода также можно рассматривать как вероятность перехода к контекстной модели меньшего порядка.
лишь предсказывает значение символа, непосредственное сжатие осуществляется алгоритмами энтропийного кодирования, как например, алгоритм Хаффмана или арифметическое кодирование.
Пример
Кодирование
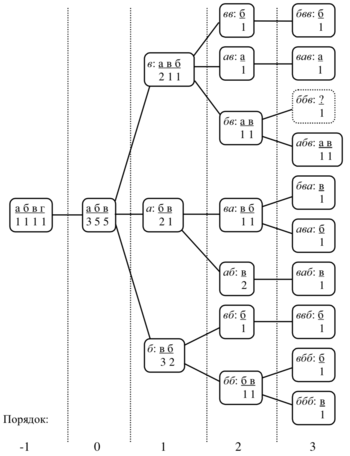
Имеется последовательность символов алфавита , которая уже была закодирована.
Пусть счетчик символа ухода равен единице для всех , при обновлении модели счетчики символов увеличиваются на единицу во всех активных , применяется метод исключения и максимальная длина контекста равна трем, т. е. . Первоначально модель состоит из , в которой счетчики всех четырех символов алфавита имеют значение . Состояние модели обработки последовательности представлено на , где прямоугольниками обозначены контекстные модели, при этом для каждой КМ указан курсивом контекст, а также встречавшиеся в контексте символы и их частоты.
| «» | |||||||
| «» | |||||||
| «» | |||||||
| «» |
Пусть текущий символ равен «», т. е. «» = «», тогда процесс его кодирования будет выглядеть следующим образом. Сначала рассматривается контекст -го порядка . Ранее он не встречался, поэтому кодер, ничего не послав на выход, переходит к анализу статистики для контекста -го порядка. В этом контексте () встречались символ «» и символ «», счетчики которых в соответствующей равны каждый, поэтому символ ухода кодируется с вероятностью , где в знаменателе число — наблюдавшаяся частота появления контекста , — значение счетчика символа ухода. В контексте -го порядка «» дважды встречался символ «», который исключается (маскируется), один раз также исключаемый «» и один раз «», поэтому оценка вероятности ухода будет равна . В символ «» также оценить нельзя, причем все имеющиеся в этой символы «», «», «» исключаются, так как уже встречались нам в более высокого порядка. Поэтому вероятность ухода получается равной единице. Цикл оценивания завершается на уровне , где «» к этому времени остается единственным до сих пор не попавшимся символом, поэтому он получает вероятность и кодируется посредством бит. Таким образом, при использовании хорошего статистического кодировщика для представления «» потребуется в целом примерно бит. Перед обработкой следующего символа создается для строки и производится модификация счетчиков символа «» в созданной и во всех просмотренных . В данном случае требуется изменение всех порядков от до .
Декодирование
Алгоритм декодирования абсолютно симметричен алгоритму кодирования. После декодирования символа в текущей проверяется, не является ли он символом ухода; если это так, то выполняется переход к порядком ниже. Иначе считается, что исходный символ восстановлен, он записывается в декодированный поток и осуществляется переход к следующему шагу. Содержание процедур обновления счетчиков, создания новых контекстных моделей, прочих вспомогательных действий и последовательность их применения должны быть строго одинаковыми при кодировании и декодировании. Иначе возможна рассинхронизация копий модели кодера и декодера, что рано или поздно приведет к ошибочному декодированию какого-то символа. Начиная с этой позиции вся оставшаяся часть сжатой последовательности будет разжата неправильно. Разница между кодами символов, оценки вероятности которых одинаковы, достигается за счет того, что -предсказатель передает кодировщику так называемые накопленные частоты (или накопленные вероятности) оцениваемого символа и его соседей или кодовые пространства символов. Так, например, для контекста можно составить следующую таблицу:
| «» | ||||
| «» | ||||
| «» | ||||
| «» | ||||
| «» |
Хороший кодировщик должен отобразить символ «» с оценкой вероятности в код длины , что и обеспечит сжатие всей обрабатываемой последовательности в целом.
Проблема нулевой частоты
| Определение: |
| Проблема нулевой частоты (zero frequency problem) — проблема обработки новых символов, ещё не встречавшихся во входном потоке. |
На сегодняшний день можно выделить два подхода к решению этой проблемы: априорные методы, основанные на предположениях о природе сжимаемых данных, и адаптивные методы, которые пытаются приспособиться к сжимаемым данным.
Априорные методы
Выедем следующие обозначения:
- — общее число просмотров контекста
- — количество разных символов в контексте
- — количество таких разных символов, что они встречались в контексте ровно раз
- — (оценка вероятности кода ухода) по методу
Изобретатели алгоритма предложили два метода : так называемые метод и метод . Частные случаи алгоритма с использованием этих методов называются, соответственно, и .
Затем был разработан метод , а в след за ним метод :
Адаптивные методы
| Определение: |
| SEE (Secondary Escape Estimation) — модель оценки, которая адаптируется к обрабатываемым данным. |
Для нахождения строятся (Escape Context), формируемые из различный полей. Всего используется поля, в которых содержится информация о:
- порядке контекста
- количестве уходов
- количестве успешных кодирований
- последних двух символах контекста
для текущего контекста находится путем взвешивания оценок, которые дают три контекста ухода (, , ), соответствующие текущему контексту. наиболее точно соответствует текущему контексту, контексты ухода порядком ниже формируются путем выбрасывания части информации полей . При взвешивании контекстов ухода используются следующие веса :
, где , которую дает данный взвешиваемый контекст.
Величину, которая формируется из фактического количества успешных кодирований и количества уходов в -контекстах, соответствующих этому обозначим как .