Кворум рушащейся стенки — различия между версиями
(Новая страница: «Категория: Параллельное программирование '''Кворум рушащейся стенки''' - пример [[Кворум|к…») |
м (rollbackEdits.php mass rollback) |
||
| (не показано 5 промежуточных версий 5 участников) | |||
| Строка 1: | Строка 1: | ||
[[Категория: Параллельное программирование]] | [[Категория: Параллельное программирование]] | ||
| − | '''Кворум рушащейся стенки''' | + | '''Кворум рушащейся стенки''' (Crumbling walls quorum) — пример [[Кворум|кворума]] с подмножествами размера порядка $O(\sqrt n)$ вместо $O(n)$, как у [[Кворум простого большинства|кворума простого большинства]]. |
| − | Процессы упорядочены в линии по возможности | + | Структура: |
| − | + | # Процессы упорядочены в линии, по возможности равной длины. | |
| + | # Минимальный элемент кворума — объединение всех процессов какой-то одной линии плюс по одному представителю из каждой линии ниже. | ||
| + | |||
| + | === Пример === | ||
| + | |||
| + | |||
| + | {|border="1" | ||
| + | |P1 | ||
| + | |P2 | ||
| + | |P3 | ||
| + | |- | ||
| + | |P4 | ||
| + | |P5 | ||
| + | |P6 | ||
| + | |- | ||
| + | |P7 | ||
| + | |P8 | ||
| + | |P9 | ||
| + | |} | ||
| + | |||
| + | Тогда кворумом может являться такое семейство (если замкнуть его по взятию надмножества): | ||
| + | * {1, 2, 3, 4, 9} | ||
| + | * {4, 5, 6, 8} | ||
| + | * {7, 8, 9} | ||
| + | |||
| + | === Большой пример === | ||
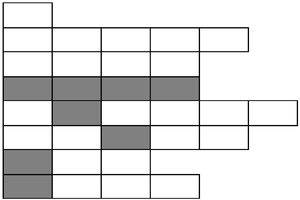
| + | Если у нас есть 32 процесса, то можно выбрать вот такой кворум из 8 процессов (пример из статьи "Crumbling walls: a class of practical and efficient quorum systems" от D Peleg): | ||
| + | |||
| + | [[Файл:crumbling-walls.png|300px]] | ||
Текущая версия на 19:20, 4 сентября 2022
Кворум рушащейся стенки (Crumbling walls quorum) — пример кворума с подмножествами размера порядка $O(\sqrt n)$ вместо $O(n)$, как у кворума простого большинства.
Структура:
- Процессы упорядочены в линии, по возможности равной длины.
- Минимальный элемент кворума — объединение всех процессов какой-то одной линии плюс по одному представителю из каждой линии ниже.
Пример
| P1 | P2 | P3 |
| P4 | P5 | P6 |
| P7 | P8 | P9 |
Тогда кворумом может являться такое семейство (если замкнуть его по взятию надмножества):
- {1, 2, 3, 4, 9}
- {4, 5, 6, 8}
- {7, 8, 9}
Большой пример
Если у нас есть 32 процесса, то можно выбрать вот такой кворум из 8 процессов (пример из статьи "Crumbling walls: a class of practical and efficient quorum systems" от D Peleg):