Лемма о рукопожатиях — различия между версиями
(Значок суммы..) |
м (rollbackEdits.php mass rollback) |
||
| (не показано 56 промежуточных версий 10 участников) | |||
| Строка 1: | Строка 1: | ||
| − | == | + | == Неориентированный граф == |
| − | Сумма степеней всех вершин графа (или мультиграфа без петель) — | + | {{Лемма |
| − | + | |statement= | |
| + | Сумма степеней всех вершин графа (или мультиграфа без петель) — чётное число, равное удвоенному числу рёбер: | ||
| + | <br /> <tex> \sum\limits_{v\in V(G)} deg\ v=2\cdot|E(G)|</tex> | ||
| + | |proof= | ||
| + | Возьмем пустой граф. Сумма степеней вершин такого графа равна нулю. При добавлении ребра, связывающего любые две вершины, сумма всех степеней увеличивается на 2 единицы. Таким образом, сумма всех степеней вершин чётна и равна удвоенному числу рёбер. | ||
| + | }} | ||
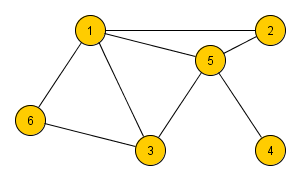
| + | Например, для следующего графа выполнено: <tex>deg(1)+\ldots+deg(6)=16=2\cdot|E|</tex> | ||
| − | {{ | + | [[Файл:undir_grap.png]] |
| − | + | ||
| − | + | '''Следствие 1.''' В любом графе число вершин нечётной степени чётно. | |
| − | + | ||
| − | + | '''Следствие 2.''' Число рёбер в полном графе <tex dpi=150>\frac{n\cdot(n-1)}{2} </tex>. | |
| − | + | ||
| − | + | <br /> | |
| + | |||
| + | == Ориентированный граф == | ||
| + | |||
| + | {{Лемма | ||
| + | |statement= | ||
| + | Сумма входящих и исходящих степеней всех вершин ориентированного графа — чётное число, равное удвоенному числу рёбер: | ||
| + | <br /> <tex>\sum\limits_{v\in V(G)} deg^{-}\ v \; + \sum\limits_{v\in V(G)} deg^{+}\ v=2\cdot |E(G)| </tex> | ||
| + | |||
| + | |proof= | ||
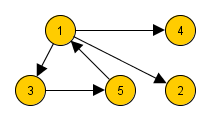
| + | [[Файл:dir_grap.png|thumb|300px| <tex>deg^{-}+deg^{+}=10=2\cdot |E|</tex>]] | ||
| + | Аналогично доказательству леммы о рукопожатиях неориентированном графе. | ||
| + | То есть возьмем пустой граф и будем добавлять в него рёбра. При этом каждое добавление ребра увеличивает на единицу сумму входящих и на единицу сумму исходящих степеней. Таким образом, сумма входящих и исходящих степеней всех вершин ориентированного графа чётна и равна удвоенному числу рёбер. | ||
}} | }} | ||
| − | '' | + | == Бесконечный граф == |
| − | В | + | [[Файл:inf_grap.png|thumb|300px|right|Пример бесконечного графа, в котором не выполняется лемма]] |
| + | |||
| + | В бесконечном графе лемма не работает, даже в случае с конечным числом вершин нечётной степени. Покажем это на примере. | ||
| + | |||
| + | При выборе бесконечного пути из вершины <tex> V </tex> (см. рисунок справа) имеем путь, в котором все вершины кроме стартовой имеют чётную степень, что противоречит следствию из леммы. | ||
| + | |||
| + | == Регулярный граф == | ||
| + | {{Определение | ||
| + | |definition= | ||
| + | Граф называется '''регулярным''', если степени всех его вершин равны. | ||
| + | }} | ||
| + | {{Утверждение | ||
| + | |statement= | ||
| + | В регулярном графе с <tex> n </tex> вершинами ровно <tex dpi=150>\frac{k\cdot n}{2} </tex> рёбер. | ||
| + | |||
| + | }} | ||
| + | |||
| + | |||
| + | |||
| + | {{Утверждение | ||
| + | |statement=Если степень каждой вершины нечётна и равна <tex> k</tex>, то количество рёбер кратно <tex> k </tex>. | ||
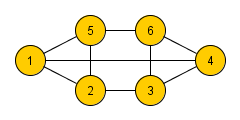
| + | |proof= [[Файл:reg_grap.png|thumb|300px|right|Регулярный граф с <tex dpi=140>\frac{k\cdot n}{2} = \frac{3\cdot 6}{2}=9 </tex> рёбрами ]] | ||
| + | Действительно, так как степень каждой вершины нечётна, то число вершин в графе чётно(так сумма степеней всех вершин чётна). Пусть <tex> n = 2\cdot r </tex>, то равенство принимает вид <tex dpi=150>|E| =\frac{k\cdot n}{2} = \frac{2\cdot k\cdot r}{2}=k\cdot r </tex>, то есть количество рёбер кратно <tex> k</tex>. | ||
| + | }} | ||
| − | + | == Источники информации == | |
| − | + | * Lecture Notes on Graph Theory By Tero Harju, Department of Mathematics University of Turku, 2011 — с. 7-8 | |
| + | * [http://en.wikipedia.org/wiki/Handshaking_lemma Handshaking lemma — Wikipedia] | ||
| + | [[Категория: Алгоритмы и структуры данных]] | ||
| + | [[Категория: Основные определения теории графов]] | ||
Текущая версия на 19:20, 4 сентября 2022
Содержание
Неориентированный граф
| Лемма: |
Сумма степеней всех вершин графа (или мультиграфа без петель) — чётное число, равное удвоенному числу рёбер:
|
| Доказательство: |
| Возьмем пустой граф. Сумма степеней вершин такого графа равна нулю. При добавлении ребра, связывающего любые две вершины, сумма всех степеней увеличивается на 2 единицы. Таким образом, сумма всех степеней вершин чётна и равна удвоенному числу рёбер. |
Например, для следующего графа выполнено:
Следствие 1. В любом графе число вершин нечётной степени чётно.
Следствие 2. Число рёбер в полном графе .
Ориентированный граф
| Лемма: |
Сумма входящих и исходящих степеней всех вершин ориентированного графа — чётное число, равное удвоенному числу рёбер:
|
| Доказательство: |
|
Аналогично доказательству леммы о рукопожатиях неориентированном графе. То есть возьмем пустой граф и будем добавлять в него рёбра. При этом каждое добавление ребра увеличивает на единицу сумму входящих и на единицу сумму исходящих степеней. Таким образом, сумма входящих и исходящих степеней всех вершин ориентированного графа чётна и равна удвоенному числу рёбер. |
Бесконечный граф
В бесконечном графе лемма не работает, даже в случае с конечным числом вершин нечётной степени. Покажем это на примере.
При выборе бесконечного пути из вершины (см. рисунок справа) имеем путь, в котором все вершины кроме стартовой имеют чётную степень, что противоречит следствию из леммы.
Регулярный граф
| Определение: |
| Граф называется регулярным, если степени всех его вершин равны. |
| Утверждение: |
В регулярном графе с вершинами ровно рёбер. |
| Утверждение: |
Если степень каждой вершины нечётна и равна , то количество рёбер кратно . |
| Действительно, так как степень каждой вершины нечётна, то число вершин в графе чётно(так сумма степеней всех вершин чётна). Пусть , то равенство принимает вид , то есть количество рёбер кратно . |
Источники информации
- Lecture Notes on Graph Theory By Tero Harju, Department of Mathematics University of Turku, 2011 — с. 7-8
- Handshaking lemma — Wikipedia