Производные некоторых элементарных функций — различия между версиями
Komarov (обсуждение | вклад) (Добавлен рисунок) |
м (rollbackEdits.php mass rollback) |
||
| (не показано 15 промежуточных версий 5 участников) | |||
| Строка 1: | Строка 1: | ||
| − | |||
| − | |||
== Вычисление некоторых пределов == | == Вычисление некоторых пределов == | ||
| Строка 15: | Строка 13: | ||
воспользуемся геометрическим смыслом синуса. | воспользуемся геометрическим смыслом синуса. | ||
Рассмотрим радианную меру угла <tex>\alpha</tex>, равную отношению длины дуги к радиусу окружности. | Рассмотрим радианную меру угла <tex>\alpha</tex>, равную отношению длины дуги к радиусу окружности. | ||
| − | В частности, при <tex>1</tex>, длина дуги совпадает с величиной угла. | + | В частности, при <tex>r = 1</tex>, длина дуги совпадает с величиной угла. |
<tex>0 \leq x \le \frac\pi2</tex> | <tex>0 \leq x \le \frac\pi2</tex> | ||
| − | Сектор <tex> | + | Сектор <tex>AOB \subset \triangle AOD</tex> |
| − | + | <tex>\sin x = |BC| \leq AB < \buildrel \smile \over{AB} = x</tex> | |
| − | <tex>\sin x = |BC| \leq AB < \ | ||
<tex>\sin x < x \Rightarrow \frac{\sin x}x < 1</tex>. Запомним этот факт. | <tex>\sin x < x \Rightarrow \frac{\sin x}x < 1</tex>. Запомним этот факт. | ||
| − | + | Площадь сектора <tex>{AOB}</tex> равна <tex>\frac{x}2</tex>, | |
| + | а <tex>S_{\triangle AOD}= \frac12 \operatorname{tg} x</tex>. | ||
| − | <tex>\frac{ | + | Тогда |
| − | + | <tex>\frac{x}{2} \leq S_{\triangle AOD} = | |
| + | \frac12 \operatorname{tg} x | ||
| + | = \frac12 \frac{\sin x}{\cos x} | ||
| + | \Rightarrow \cos x \leq \frac{\sin x}{x}</tex> | ||
Но тогда, <tex>\cos x \leq \frac{\sin x}{x} \leq 1</tex>. | Но тогда, <tex>\cos x \leq \frac{\sin x}{x} \leq 1</tex>. | ||
| Строка 38: | Строка 39: | ||
}} | }} | ||
| − | === | + | === Второй замечательный предел === |
{{Определение | {{Определение | ||
|definition= | |definition= | ||
| − | <tex>e = \lim\limits_{n \to \infty} \left(1 + \frac1n \right) ^ n</tex> | + | <tex dpi=150>e = \lim\limits_{n \to \infty} \left(1 + \frac1n \right) ^ n</tex> |
}} | }} | ||
| − | Из этого, подставив <tex>x = \frac1n</tex> <tex>\lim\limits_{x \to 0} (1 + x)^{\frac{1}{x}}</tex> | + | Из этого, подставив <tex>x = \frac1n</tex>, получим |
| + | |||
| + | <tex dpi= "150">\lim\limits_{x \to 0} (1 + x)^{\frac{1}{x}} = e</tex> | ||
Далее, прологарифмировав последнее равенство, получим: | Далее, прологарифмировав последнее равенство, получим: | ||
| − | <tex>\frac{\ | + | <tex>\frac{\ln(1 + x)}x</tex> при <tex>x \to 0</tex> стремится к <tex>1</tex>. |
=== (e^x - 1)/x === | === (e^x - 1)/x === | ||
| Строка 54: | Строка 57: | ||
{{Утверждение | {{Утверждение | ||
|statement= | |statement= | ||
| − | <tex>\frac{e^x - 1}x \to 1</tex> при <tex>x \to 0</tex> | + | <tex dpi= "150">\frac{e^x - 1}x \to 1</tex> при <tex>x \to 0</tex> |
|proof= | |proof= | ||
| − | <tex>\frac{e^x - 1}{x}</tex>(подставив <tex>t = e^x - 1</tex>) <tex> = \frac{t}{\ln (1 + t)}</tex>. | + | <tex dpi= "150">\frac{e^x - 1}{x}</tex>(подставив <tex>t = e^x - 1</tex>) |
| − | + | <tex> = \frac{t}{\ln (1 + t)}</tex>. | |
| + | |||
| + | Тогда | ||
| + | <tex>\frac{\ln (1 + x)}{x} \xrightarrow[x \to 0]{} 1 \Rightarrow \frac{t}{\ln (1 + t)} \xrightarrow[t \to 0]{} 1</tex> | ||
}} | }} | ||
| − | Рассмотрим выражение <tex>\frac{x^ | + | Рассмотрим выражение <tex dpi= "150"> \frac{(1+x)^m - 1}{mx}, \ x \to 0 </tex>. Оно (?)создаёт неопределённость <tex>\frac00</tex>. При этом, предел нельзя |
вычислить переходом к нему в числителе и знаменателе по отдельности. Этот предел подстановкой сводится к предыдущим. | вычислить переходом к нему в числителе и знаменателе по отдельности. Этот предел подстановкой сводится к предыдущим. | ||
| Строка 91: | Строка 97: | ||
| − | ==== 1/n {{---}} целое ==== | + | ==== 1/n; n {{---}} целое ==== |
{{Утверждение | {{Утверждение | ||
|statement= | |statement= | ||
| − | Посчитаем <tex>y' = (x^{\frac1n})' = \frac1n x^{\frac1n - 1}, \ n \in \mathbb{N}</tex> | + | Посчитаем <tex dpi= "150">y' = (x^{\frac1n})' = \frac1n x^{\frac1n - 1}, \ n \in \mathbb{N}</tex> |
|proof= | |proof= | ||
Согласно формуле дифференцирования обратной функции, <tex>x' = (y^n)' = n y^{n - 1}</tex>. | Согласно формуле дифференцирования обратной функции, <tex>x' = (y^n)' = n y^{n - 1}</tex>. | ||
| − | <tex>y' = \frac{1}{x'} = \frac1{ny^{n - 1}} = \frac1n | + | <tex dpi= "150">y' = \frac{1}{x'} = \frac1{ny^{n - 1}} = \frac1n y^{1 - n} = \frac1n \left(x^{\frac1n}\right)^{1 - n} = \frac1n x^{\frac1n - 1}</tex> |
}} | }} | ||
| Строка 110: | Строка 116: | ||
<tex>(x ^ {\alpha})', \ \alpha \in \mathbb{Q}</tex>. | <tex>(x ^ {\alpha})', \ \alpha \in \mathbb{Q}</tex>. | ||
|proof= | |proof= | ||
| − | <tex>(x^{\frac{n}{m}})'</tex>(подставив <tex>t = x^{\frac 1m}</tex>) <tex> = n t^{ | + | <tex dpi= "150">(x^{\frac{n}{m}})'</tex>(подставив <tex>t = x^{\frac 1m}</tex>) <tex> = n t^{n - 1} \frac 1m x ^ {\frac1m - 1} = \frac{n}{m} x ^ {\frac{n}{m} - 1}</tex> |
}} | }} | ||
| Строка 126: | Строка 132: | ||
<tex>\Delta y = e^{x + \Delta x} - e^x = e^x(e^{\Delta x} - 1)</tex> | <tex>\Delta y = e^{x + \Delta x} - e^x = e^x(e^{\Delta x} - 1)</tex> | ||
| − | Тогда <tex>\frac{\Delta y}{\Delta x} = e^x \cdot \frac{e^{\Delta x} - 1}{\Delta x}</tex>. | + | Тогда <tex dpi= "150">\frac{\Delta y}{\Delta x} = e^x \cdot \frac{e^{\Delta x} - 1}{\Delta x}</tex>. |
Ранее мы доказали, что <tex>\frac{e^x - 1}{x} \xrightarrow[x\to 0]{} 1</tex>. | Ранее мы доказали, что <tex>\frac{e^x - 1}{x} \xrightarrow[x\to 0]{} 1</tex>. | ||
| Строка 144: | Строка 150: | ||
<tex>x = e^y</tex>. Тогда <tex>x' = e^y</tex>. | <tex>x = e^y</tex>. Тогда <tex>x' = e^y</tex>. | ||
| − | <tex>y' = \frac{1}{x'} = \frac{1}{e^y} = \frac{1}{e^{\ln x}} = \frac1x</tex> | + | <tex dpi= "150">y' = \frac{1}{x'} = \frac{1}{e^y} = \frac{1}{e^{\ln x}} = \frac1x</tex> |
}} | }} | ||
| Строка 158: | Строка 164: | ||
<tex>\Delta y = \sin(x + \Delta x) - \sin(x) = 2 \sin\left(\frac{\Delta x}{2}\right) \cos\left(x + \frac{\Delta x}{2}\right)</tex> | <tex>\Delta y = \sin(x + \Delta x) - \sin(x) = 2 \sin\left(\frac{\Delta x}{2}\right) \cos\left(x + \frac{\Delta x}{2}\right)</tex> | ||
| − | <tex>\frac{\Delta y}{\Delta x} = \frac{\sin\left(\frac{\Delta x}{2}\right)}{\frac{\Delta x}{2}} \cdot \cos\left(x + \frac{\Delta x}{2} \right)</tex> | + | <tex dpi= "150">\frac{\Delta y}{\Delta x} = \frac{\sin\left(\frac{\Delta x}{2}\right)}{\frac{\Delta x}{2}} \cdot \cos\left(x + \frac{\Delta x}{2} \right)</tex> |
Первый множитель, равный вычисленному ранее пределу, равен <tex>1</tex>, а второй при <tex>\Delta x \to 0</tex> стремится к <tex>\cos x</tex>. | Первый множитель, равный вычисленному ранее пределу, равен <tex>1</tex>, а второй при <tex>\Delta x \to 0</tex> стремится к <tex>\cos x</tex>. | ||
| Строка 170: | Строка 176: | ||
{{Утверждение | {{Утверждение | ||
|statement= | |statement= | ||
| − | <tex>\arcsin' x = \frac{1}{\sqrt{1 - x^2}}, \ y \in \left[-\frac{ | + | <tex dpi= "150">\arcsin' x = \frac{1}{\sqrt{1 - x^2}}, \ y \in \left[-\frac{\pi}{2}; \frac{\pi}{2} \right]</tex> |
|proof= | |proof= | ||
<tex>y = \arcsin x \Rightarrow x = \sin y</tex>. Тогда <tex>x' = \cos x</tex>. | <tex>y = \arcsin x \Rightarrow x = \sin y</tex>. Тогда <tex>x' = \cos x</tex>. | ||
| − | Так как <tex>\cos(\arcsin(x)) \ | + | Так как <tex>\cos(\arcsin(x)) \geq 0</tex>, то |
| + | <tex dpi= "150">y' = \frac{1}{\cos y} = \frac{1}{\cos \arcsin x} = \frac{1}{\sqrt{1 - \sin^2 (\arcsin x)}} = \frac{1}{\sqrt{1 - x^2}}</tex> | ||
| − | Получаем <tex>\arcsin' x = \frac{1}{\sqrt{1 - x^2}}</tex>. | + | Получаем <tex dpi= "150">\arcsin' x = \frac{1}{\sqrt{1 - x^2}}</tex>. |
}} | }} | ||
[[Категория:Математический анализ 1 курс]] | [[Категория:Математический анализ 1 курс]] | ||
Текущая версия на 19:27, 4 сентября 2022
Содержание
Вычисление некоторых пределов
Вычислим предварительно ряд важных пределов.
Первый замечательный предел
| Утверждение: |
|
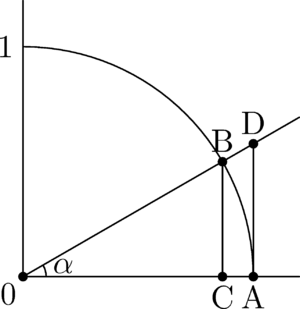
В теории степенных рядов синус определён как сумма ряда. Сейчас для доказательства, однако, воспользуемся геометрическим смыслом синуса. Рассмотрим радианную меру угла , равную отношению длины дуги к радиусу окружности. В частности, при , длина дуги совпадает с величиной угла.
Сектор
. Запомним этот факт. Площадь сектора равна , а . Тогда Но тогда, . Но так как Тогда . |
Второй замечательный предел
| Определение: |
Из этого, подставив , получим
Далее, прологарифмировав последнее равенство, получим: при стремится к .
(e^x - 1)/x
| Утверждение: |
при |
|
(подставив ) . Тогда |
Рассмотрим выражение . Оно (?)создаёт неопределённость . При этом, предел нельзя
вычислить переходом к нему в числителе и знаменателе по отдельности. Этот предел подстановкой сводится к предыдущим.
Вычисление производных некоторых функций
y = x^n
n — целое
| Утверждение: |
|
Докажем по индукции.
Это соответствует функции . Тогда Тогда
|
Заметим, что если непрерывна и монотонна в окрестности , а также, , то обратная функция дифференцируема в , и её производная равна . Это следует из того факта, что .
1/n; n — целое
| Утверждение: |
Посчитаем |
|
Согласно формуле дифференцирования обратной функции, . |
Подведём промежуточный итог. Мы научились считать
n — рациональное
| Утверждение: |
. |
| (подставив ) |
Важное Замечание: — не степенная функция. Все реальные пацаны считают это по определению равным
e^x
| Утверждение: |
|
Тогда . Ранее мы доказали, что . Тогда . Это единственная функция, которая обладает таким свойством(это просто забавный факт, его не надо доказывать). Именно поэтому занимает такое важное место в математике. |
ln(x)
| Утверждение: |
|
. Тогда . |
sin(x)
| Утверждение: |
|
Пусть .
Первый множитель, равный вычисленному ранее пределу, равен , а второй при стремится к . Тогда . |
arcsin(x)
| Утверждение: |
|
. Тогда . Так как , то Получаем . |