|
Пусть [math]G_{set}(g, n, k)[/math] — семейство всех графов с [math]n[/math] вершинами, обхватом [math]g[/math] и максимальной степенью вершин не более [math]k[/math]. При [math]n \gt g[/math] очевидно, что [math]G_{set}(g, n, k) \neq \emptyset[/math]: например, этому множеству принадлежит граф, состоящий из простого цикла на [math]g[/math] вершинах и [math]n - g[/math] изолированных вершин.
Пусть [math]v_{\lt k}(G)[/math] — количество вершин степени меньше [math]k[/math] в графе [math]G[/math], а [math]dist_{\lt k}(G)[/math] — максимальное из расстояний между парами вершин степени менее [math]k[/math] в графе [math]G[/math]. (при [math]v_{\lt k}(G) \lt 2[/math], положим [math]dist_{\lt k}(G) = 0[/math]). Выберем в [math]G_{set}(g, n, k)[/math] граф следующим образом: сначала выберем все графы с максимальным количеством рёбер, затем из них выберем графы с максимальным [math]v_{\lt k}[/math], и, наконец, из оставшихся выберем граф [math]G[/math] c максимальным [math]dist_{\lt k}(G)[/math]. Если таких графов несколько, выберем любой.
Докажем, что [math]G[/math] — регулярный граф степени [math]k[/math].
Предположим, что это не так и рассмотрим пару его максимально удаленных вершин степени менее [math]k[/math]: пусть это будут вершины [math]x[/math] и [math]y[/math] (если вершина степени менее [math]k[/math] в графе всего одна, то [math]x =
y[/math]).
-
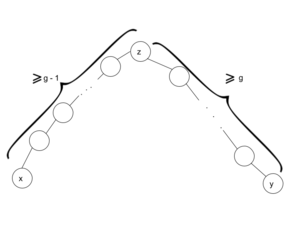 Расположение вершины [math]z[/math] относительно вершин [math]x[/math] и [math]y[/math]
- Так [math]d_G(x), d_G(y) \leqslant k - 1 [/math], а степени остальных вершин графа не более [math]k[/math], то по лемме существует такая вершина [math]z[/math], что [math]dist(x, z) \geqslant g - 1[/math] и [math]dist(y, z) \geqslant g[/math].
- [math]d_G(z) \lt k[/math]. В таком случае, [math]d_G(z) \lt k, d_G(y) \lt k, dist_G(y, z) \geqslant g[/math], что невозможно, согласно пункту 1. В таком случае:
- [math]d_G(z) = k \geqslant 3[/math], следовательно, существует ребро [math]zu \in E(G)[/math], через которое проходят не все простые циклы длины [math]g[/math] графа [math]G[/math], тогда [math]g(G \setminus zu) = g(G) = g[/math]
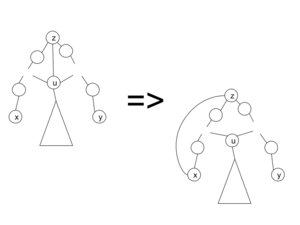 Получение графа [math]G'[/math] из графа [math]G[/math]Пусть [math]G' = G \setminus zu \cup zx[/math]. Тогда из
[math] dist_G(y, u) \geqslant dist_G(y, z) - 1 \geqslant g - 1 \gt dist_G(x, y) = dist_{\lt k}(G) ~~~ \textbf{(1)} [/math].
следует, что [math]d_G(u) = k[/math].
[math]g(G') = g(G) = g, |E(G')| = |e(G)| - 1 + 1 = |E(G)| [/math]. Тогда
[math] d_{G'}(x) = d_G(x) + 1 \leqslant k, d_{G'}(u) = d_G(u) - 1 = k - 1 ~~~ \textbf{(2)} [/math].
Степени всех остальных вершин в [math]G[/math] и [math]G'[/math] совпадают. Тогда [math]G' \in G_{set}(g, n, k)[/math]. Из [math]\textbf{(2)}[/math] следует, что [math]v_{\lt k}(G') \geqslant v_{\lt k}(G)[/math]. Тогда ввиду выбора графа [math]G[/math] должно быть [math]v_{\lt k}(G') = v_{\lt k}(G)[/math], что возможно лишь при [math]d_{G'}(x) = k[/math] и [math]d_G(x) = k - 1[/math]. Так как [math]kn[/math] чётно, вершина [math]x[/math] не может быть единственной вершиной степени менее [math]k[/math] в графе [math]G[/math], поэтому [math]x \neq y[/math].
Докажем, что [math]dist_{G'}(y, u) \gt dist_{G}(y, x)[/math]. Действительно, рассмотрим путь [math]P: y \leadsto u[/math], который реализует расстояние между [math]y[/math] и [math]u[/math] в [math]G'[/math]. Если [math]P[/math] проходит только по рёбрам [math]G[/math], то, учитывая [math]\textbf{(1)}[/math], получаем
[math] dist_{G'}(y, u) = dist_G(y, u) \geqslant g - 1 \gt dist_G(y, x) [/math]
Значит, [math]P[/math] проходит по ребру [math]zx[/math]. Следовательно, [math]P[/math] содержит путь по рёбрам графа [math]G[/math] от [math]y[/math] до одной из вершин [math]x[/math] или [math]z[/math] и ребро [math]xz[/math]. Тогда
[math] dist_{G'}(y, u) = \min(dist_G(y, x), dist_G(y, z)) + 1 \gt dist_G(y, x) [/math],
так как [math]dist_G(y, z) \geqslant g \gt dist_G(y, x)[/math]. Таким образом
[math] dist_{\lt k}(G') \geqslant dist_{G'}(y, u) \gt dist_G(y, x) dist_{\lt k}(G) [/math]
Получили противоречие с принципом выбора графа [math]G[/math], что доказывает, что [math]G[/math] — [math]k[/math]-регулярный. |