J2ni2Cmax — различия между версиями
Watson (обсуждение | вклад) (→Доказательство корректности алгоритма) |
м (rollbackEdits.php mass rollback) |
||
| (не показана 41 промежуточная версия 5 участников) | |||
| Строка 1: | Строка 1: | ||
| − | == | + | <tex dpi = 200>J2 \mid n_i \leqslant 2 \mid C_{max}</tex> |
| − | Рассмотрим задачу: | + | {{Задача |
| − | + | |definition=Рассмотрим задачу: | |
| − | + | *Дано <tex>n</tex> работ и <tex>2</tex> станка. | |
| − | + | *Для каждой работы известно её время выполнения на каждом станке <tex>p_{ij}</tex>. | |
| − | + | *Для каждой работы известна последовательность <tex>O_{i1}, \ O_{i2} \ \ldots \ O_{ik}</tex> станков {{---}} порядок, в котором нужно выполнить работу. | |
| − | + | *В каждой последовательности <tex>O_{i}</tex> не более двух элементов. | |
| − | + | Требуется минимизировать время окончания выполнения всех работ. }} | |
| − | |||
| − | Требуется минимизировать время окончания выполнения всех работ. | ||
==Описание алгоритма== | ==Описание алгоритма== | ||
| − | <tex>M_{1}</tex> - первый станок. <tex>M_{2}</tex> - второй станок. | + | <tex>M_{1}</tex> {{---}} первый станок. <tex>M_{2}</tex> {{---}} второй станок. |
Разобьем все работы на четыре множества: | Разобьем все работы на четыре множества: | ||
| − | + | #<tex>I_{1}</tex> {{---}} множество всех работ, которые должны выполниться только на <tex>M_{1}</tex>. | |
| − | + | #<tex>I_{2}</tex> {{---}} множество всех работ, которые должны выполниться только на <tex>M_{2}</tex>. | |
| − | + | #<tex>I_{12}</tex> {{---}} множество всех работ, которые должны выполниться сначала на <tex>M_{1}</tex> затем на <tex>M_{2}</tex>. | |
| − | + | #<tex>I_{21}</tex> {{---}} множество всех работ, которые должны выполниться сначала на <tex>M_{2}</tex> затем на <tex>M_{1}</tex>. | |
| − | + | Решим задачу [[F2Cmax|<tex>F2 \mid \mid C_{max}</tex>]] для <tex>I_{12}</tex> и для <tex>I_{21}</tex> независимо. Получим расписание <tex>S_{12}</tex> и <tex>S_{21}</tex>. | |
| − | |||
| − | Решим задачу [[F2Cmax|<tex>F2 \mid \mid C_{max}</tex>]] для <tex>I_{12}</tex> и для <tex>I_{21}</tex>. Получим расписание <tex>S_{12}</tex> и <tex>S_{21}</tex>. | ||
Тогда оптимальное расписание для нашей задачи будет следующим: | Тогда оптимальное расписание для нашей задачи будет следующим: | ||
| − | + | * Расписание <tex>M_{1}</tex>: сначала <tex>I_{12}</tex> в соответсвии с расписанием <tex>S_{12}</tex>. Затем <tex>I_{1}</tex> в произвольном порядке. Затем <tex>I_{21}</tex> в соответсвии с <tex>S_{21}</tex>. | |
| − | + | * Расписание <tex>M_{2}</tex>: сначала <tex>I_{21}</tex> в соответсвии с расписанием <tex>S_{21}</tex>. Затем <tex>I_{2}</tex> в произвольном порядке. Затем <tex>I_{12}</tex> в соответсвии с <tex>S_{12}</tex>. | |
| − | + | '''Примечание''': во время выполнения <tex>I_{21}</tex> на <tex>M_{1}</tex> или <tex>I_{12}</tex> на <tex>M_{2}</tex> могут возникнуть простои | |
| − | |||
| − | Примечание: во время выполнения <tex>I_{21}</tex> на <tex>M_{1}</tex> или <tex>I_{12}</tex> на <tex>M_{2}</tex> могут возникнуть простои | ||
из-за того, что работа ещё не выполнилась на предыдущем станке. | из-за того, что работа ещё не выполнилась на предыдущем станке. | ||
==Доказательство корректности алгоритма== | ==Доказательство корректности алгоритма== | ||
| − | <tex>T_{j}(x)</tex> - время выполнения множества работ <tex>x</tex> на станке <tex>j</tex>. | + | <tex>T_{j}(x)</tex> {{---}} время выполнения множества работ <tex>x</tex> на станке <tex>j</tex>. |
| − | <tex>G_{j}</tex> - множество всех работ, которые нужно сделать хотя бы раз на <tex>j</tex>-м станке | + | <tex>G_{j}</tex> {{---}} множество всех работ, которые нужно сделать хотя бы раз на <tex>j</tex>-м станке, то есть <tex>G_{1} = I_{1} \cup I_{12} \cup I_{21}</tex>. |
{{Лемма | {{Лемма | ||
|id=lemma1 | |id=lemma1 | ||
|statement= | |statement= | ||
| − | Расписание, построенное данным алгоритмом, обладает следующим свойством : один из станков работает без простоев. | + | Расписание, построенное данным алгоритмом, обладает следующим свойством: один из станков работает без простоев. |
|proof= | |proof= | ||
| − | Рассмотрим | + | Рассмотрим два случая: |
| − | + | #<tex>T_{1}(I_{12}) + T_{1}(I_{1}) \geqslant T_{2}(I_{21}) </tex>.<br>Тогда <tex>M_{1}</tex> работает без прерываний, т.к к моменту завершения выполнения <tex>I_{1}</tex> на <tex> M_{1} </tex> все работы <tex>I_{21}</tex> выполнены на <tex>M_{2}</tex>. | |
| − | Тогда <tex>M_{1}</tex> работает без прерываний, т.к к | + | #<tex>T_{1}(I_{12}) + T_{1}(I_{1}) < T_{2}(I_{21}) </tex>.<br>Тогда <tex>M_{2}</tex> работает без прерываний, т.к к моменту завершения выполнения <tex>I_{2}</tex> на <tex> M_{2} </tex> все работы <tex>I_{12}</tex> выполнены на <tex>M_{1}</tex> . |
| − | |||
| − | |||
| − | |||
| − | |||
}} | }} | ||
| Строка 55: | Строка 45: | ||
|proof= | |proof= | ||
[[Файл: j2ni2cmax.jpg|400px|thumb|right| | [[Файл: j2ni2cmax.jpg|400px|thumb|right| | ||
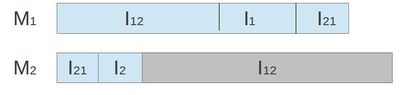
| − | Рис. 1 - Расположение работ. | + | Рис. 1 {{---}} Расположение работ. |
| − | + | <br> | |
В серой области могут быть прерывания. | В серой области могут быть прерывания. | ||
]] | ]] | ||
| Строка 63: | Строка 53: | ||
Пусть, для опеределенности <tex>M_{1}</tex> работает без прерываний. | Пусть, для опеределенности <tex>M_{1}</tex> работает без прерываний. | ||
| − | |||
| − | Иначе <tex>C_{max}</tex> достигается на <tex>M_{2}</tex>. | + | Рассмотрим станок на котором достигается <tex>C_{max}</tex> . |
| + | *Если это <tex>M_{1}</tex>, то оптимальность очевидна <tex>(C_{max} \geqslant \sum\limits_{i \in G_{1}} p_{i1})</tex>. | ||
| + | *Иначе <tex>C_{max}</tex> достигается на <tex>M_{2}</tex>. | ||
| + | Тогда либо <tex>M_{2}</tex> работает без прерываний и оптимальность очевидна. | ||
| + | Или есть прерывания. | ||
Тогда целевая функция равна ответу задачи [[F2Cmax|<tex>F2 \mid \mid C_{max}</tex>]] для работ <tex>I_{21}</tex>, который оптимален. | Тогда целевая функция равна ответу задачи [[F2Cmax|<tex>F2 \mid \mid C_{max}</tex>]] для работ <tex>I_{21}</tex>, который оптимален. | ||
| Строка 71: | Строка 64: | ||
==Сложность алгоритма== | ==Сложность алгоритма== | ||
| − | Время работы алгоритма равно времени работы алгоритма [[F2Cmax|<tex>F2 \mid \mid C_{max}</tex>]]. | + | Время работы алгоритма равно времени работы алгоритма [[F2Cmax|<tex>F2 \mid \mid C_{max}</tex>]], то есть <tex>O(n\log n)</tex>. |
| − | + | ==Источники информации== | |
| + | * Peter Brucker. «Scheduling Algorithms» {{---}} «Springer», 2006 г. {{---}} 179 {{---}} 180 стр. {{---}} ISBN 978-3-540-69515-8 | ||
[[Категория: Дискретная математика и алгоритмы]] | [[Категория: Дискретная математика и алгоритмы]] | ||
[[Категория: Теория расписаний]] | [[Категория: Теория расписаний]] | ||
Текущая версия на 19:29, 4 сентября 2022
| Задача: |
Рассмотрим задачу:
|
Содержание
Описание алгоритма
— первый станок. — второй станок.
Разобьем все работы на четыре множества:
- — множество всех работ, которые должны выполниться только на .
- — множество всех работ, которые должны выполниться только на .
- — множество всех работ, которые должны выполниться сначала на затем на .
- — множество всех работ, которые должны выполниться сначала на затем на .
Решим задачу для и для независимо. Получим расписание и .
Тогда оптимальное расписание для нашей задачи будет следующим:
- Расписание : сначала в соответсвии с расписанием . Затем в произвольном порядке. Затем в соответсвии с .
- Расписание : сначала в соответсвии с расписанием . Затем в произвольном порядке. Затем в соответсвии с .
Примечание: во время выполнения на или на могут возникнуть простои из-за того, что работа ещё не выполнилась на предыдущем станке.
Доказательство корректности алгоритма
— время выполнения множества работ на станке .
— множество всех работ, которые нужно сделать хотя бы раз на -м станке, то есть .
| Лемма: |
Расписание, построенное данным алгоритмом, обладает следующим свойством: один из станков работает без простоев. |
| Доказательство: |
|
Рассмотрим два случая:
|
Сложность алгоритма
Время работы алгоритма равно времени работы алгоритма , то есть .
Источники информации
- Peter Brucker. «Scheduling Algorithms» — «Springer», 2006 г. — 179 — 180 стр. — ISBN 978-3-540-69515-8