Сети глубокого доверия — различия между версиями
(Новая страница: «== Сети глубокого доверия == '''Сети глубокого доверия''' - это вероятностные генеративные м…») |
м (rollbackEdits.php mass rollback) |
||
| (не показаны 23 промежуточные версии 8 участников) | |||
| Строка 1: | Строка 1: | ||
| − | + | ||
| − | '''Сети глубокого доверия''' - это вероятностные генеративные модели, которые состоят из нескольких слоев стохастических скрытых переменных. Скрытые переменные обычно имеют двоичные значения и часто называются скрытыми узлами или детекторами признаков. Два верхних слоя имеют ненаправленные, симметричные связи между ними и образуют ассоциативную память. | + | '''Сети глубокого доверия''' {{---}} это вероятностные [[Порождающие модели|генеративные модели]], которые состоят из нескольких слоев стохастических скрытых переменных. Скрытые переменные обычно имеют двоичные значения и часто называются скрытыми узлами или детекторами признаков. Два верхних слоя имеют ненаправленные, симметричные связи между ними и образуют ассоциативную память. Между оставшимися парами соседних слоёв есть только направленные связи от верхнего к нижнему. Состояния узлов в нижнем слое представляют вектор данных. |
Два наиболее значимых свойства сетей глубокого доверия: | Два наиболее значимых свойства сетей глубокого доверия: | ||
| − | + | # Существует эффективная послойная процедура для обучения нисходящих весов, которая определяет, как переменные в одном слое зависят от переменных в слое выше. | |
| − | + | # После обучения скрытых переменных в каждом слое могут быть выведены значения за один проход снизу вверх, который начинается с наблюдаемого вектора данных в нижнем слое и использует веса в обратном направлении. | |
Сети глубокого доверия обучаются по одному слою за раз, обрабатывая значения скрытых переменных в одном слое в тот момент, когда они выводятся из данных для обучения следующего слоя. Это эффективное, жадное обучение может сопровождаться или сочетаться с другими процедурами обучения, которые точно настраивают все веса для улучшения генеративных или дискриминационных характеристик всей сети. | Сети глубокого доверия обучаются по одному слою за раз, обрабатывая значения скрытых переменных в одном слое в тот момент, когда они выводятся из данных для обучения следующего слоя. Это эффективное, жадное обучение может сопровождаться или сочетаться с другими процедурами обучения, которые точно настраивают все веса для улучшения генеративных или дискриминационных характеристик всей сети. | ||
| − | Дискриминирующая тонкая настройка может быть выполнена путем добавления последнего слоя переменных, которые представляют желаемые выходные данные и производные ошибок обратного распространения. Когда сети со многими скрытыми слоями применяются к высокоструктурированным входным данным, таким как изображения, обратное распространение работает намного лучше, если детекторы признаков в скрытых слоях инициализируются путем обучения глубокой сети доверия, которая моделирует структуру во входных данных. | + | Дискриминирующая тонкая настройка может быть выполнена путем добавления последнего слоя переменных, которые представляют желаемые выходные данные и производные [[Обратное распространение ошибки|ошибок обратного распространения]]. Когда сети со многими скрытыми слоями применяются к высокоструктурированным входным данным, таким как изображения, обратное распространение работает намного лучше, если детекторы признаков в скрытых слоях инициализируются путем обучения глубокой сети доверия, которая моделирует структуру во входных данных. |
== Как развивались сети глубокого доверия == | == Как развивались сети глубокого доверия == | ||
| − | В нейронных сетях первого поколения использовались | + | В нейронных сетях первого поколения использовались [[Нейронные сети, перцептрон|перцептроны]], которые идентифицировали конкретный объект или что-либо еще, принимая во внимание «вес» или предварительные свойства. Однако перцептроны могут быть эффективны только на базовом уровне и бесполезны для передовых технологий. Для решения этих проблем во втором поколении нейронных сетей была введена концепция обратного распространения, при которой полученный вывод сравнивается с желаемым выводом, а значение ошибки было снижено до нуля. [[Метод опорных векторов (SVM)|Метод опорных векторов]] позволил создать больше контрольных примеров, ссылаясь на ранее введенные контрольные примеры. Затем последовали циклические графы, называемые сетями доверия, которые помогли в решении проблем, связанных с выводом и проблемами обучения. За этим последовали сети глубокого доверия, которые помогли создать непредвзятые значения для хранения в конечных узлах. |
== Композиция простых обучающих модулей == | == Композиция простых обучающих модулей == | ||
| − | Глубокая сеть доверия может рассматриваться как набор простых обучающих модулей, каждый из которых представляет собой ограниченную машину Больцмана | + | [[Файл:Rbmimage4.png |400px|thumb| right| Рис. 1 Распределение restricted Boltzmann machine]] |
| − | + | Глубокая сеть доверия может рассматриваться как набор простых обучающих модулей, каждый из которых представляет собой ограниченную машину Больцмана<ref>[https://ru.wikipedia.org/wiki/%D0%9E%D0%B3%D1%80%D0%B0%D0%BD%D0%B8%D1%87%D0%B5%D0%BD%D0%BD%D0%B0%D1%8F_%D0%BC%D0%B0%D1%88%D0%B8%D0%BD%D0%B0_%D0%91%D0%BE%D0%BB%D1%8C%D1%86%D0%BC%D0%B0%D0%BD%D0%B0 restricted Boltzmann machine, RBM]</ref>, которая содержит слой видимых узлов, представляющий данные, и слой скрытых узлов, которые обучаются представлению особенностей, которые захватывают более высокие порядки корреляции в данных. Ограниченные машины Больцмана могут быть сложены и обучены [[Теорема Радо-Эдмондса (жадный алгоритм)|жадным алгоритмом]], чтобы сформировать так называемые глубокие сети доверия, которые моделируют совместное распределение между наблюдаемым вектором <math>x</math> и скрытыми слоями <math>h^{k}</math> следующим образом: | |
| − | [[Файл: | + | <center><tex>P(x, h^1, \ldots, h^l)=\left( \prod\limits_{k = 0}^{l - 2}P(h^k|h^{k + 1}) \right) P(h^{l - 1}|h^l)</tex>,</center> |
| + | где $x=h^0$, $P(h^{k-1}|h^{k})$ {{---}} условное распределение для видимых узлов, обусловленных скрытыми узлами RBM на уровне <math>k</math>, и $P(h^{l - 1}|h^l)$ {{---}} это видимое-скрытое совместное распределение в RBM верхнего уровня. Это показано на рисунке 1. | ||
| + | |||
| + | |||
| + | |||
| + | == Ограниченная машина Больцмана (RBM) == | ||
| + | [[Файл:Bolcman.jpg |400px| thumb | right |Рис 2. Визуализация RBM]] | ||
| + | Если вы знаете, что такое факторный анализ, то RBM можно рассматривать как двоичную версию факторного анализа. Таким образом, вместо множества факторов, определяющих вывод, мы можем иметь двоичную переменную в форме 0 или 1. | ||
| + | |||
| + | Например: если вы читаете книгу, а затем судите эту книгу по двухзначной шкале: это либо вам нравится книга, либо вам не нравится книга. В таких сценариях мы можем использовать RBM, которые помогут нам определить причину, по которой мы делаем такой выбор. | ||
| + | |||
| + | RBM используют вероятностный подход для нейронных сетей, и поэтому их также называют стохастическими нейронными сетями. | ||
| + | Если мы разложим RBM, то становится ясно, что они состоят из трех частей: | ||
| + | # Один входной слой, так называемые "Видимые узлы". | ||
| + | # Один скрытый слой. | ||
| + | # Узлы смещения. | ||
| + | В приведенном выше примере видимые узлы {{---}} это не что иное, как то, нравится ли вам книга или нет. Скрытые узлы помогают найти то, что заставило вас одобрить эту книгу. Узлы смещения добавлены, чтобы включить различные виды свойств, разных книг. | ||
| + | Простая визуализация Ограниченной машины Больцмана показана на рисунке 2. | ||
| + | |||
| + | Зеленым отмечены видимые узлы, красным скрытые, а белые узлы с меткой "bias" соответствуют узлам смещения. | ||
| + | |||
| + | Сети глубокого доверия имеют две фазы: | ||
| + | # Фаза предварительного обучения. | ||
| + | # Фаза тонкой настройки. | ||
| + | Фаза предварительного обучения {{---}} это не что иное, как несколько уровней RBN, в то время как фаза тонкой настройки {{---}} это нейронная сеть с прямой связью. Визуализация обеих фаз показана на рисунке 3 ниже | ||
| + | [[Файл:Vis2f.png |600px|thumb| center| Рис. 3 Визуализация фаз RBM]] | ||
| + | |||
| + | Алгоритм обучения глубокой сети доверия, состоит из нескольких этапов: | ||
| + | # Нахождение признаков видимых узлов, используя алгоритм контрастной дивергенции. | ||
| + | # Нахождение скрытых признаков объектов, найденных в предыдущем шаге. | ||
| + | |||
| + | == Реализация == | ||
| + | Мы начнем с определения класса для глубокой сети доверия, который назовем DBN (Deep belief network), который будет хранить уровни многослойного перцептрона MLP (Multilayer perceptron) вместе со связанными с ними RBM. Поскольку мы используем RBM для инициализации MLP, код будет отражать эту идею, насколько это возможно. Далее будут приведены RBM, используемые для инициализации сети, и MLP, используемый для классификации. | ||
| + | from __future__ import print_function, division | ||
| + | import os | ||
| + | import sys | ||
| + | import timeit | ||
| + | import numpy | ||
| + | import theano | ||
| + | import theano.tensor as T | ||
| + | |||
| + | from theano.sandbox.rng_mrg import MRG_RandomStreams | ||
| + | from logistic_sgd import LogisticRegression, load_data | ||
| + | from mlp import HiddenLayer | ||
| + | from rbm import RBM | ||
| + | |||
| + | class DBN(object): | ||
| + | def __init__(self, numpy_rng, theano_rng=None, n_ins=784, hidden_layers_sizes=[500, 500], n_outs=10): | ||
| + | self.sigmoid_layers = [] | ||
| + | self.rbm_layers = [] | ||
| + | self.params = [] | ||
| + | self.n_layers = len(hidden_layers_sizes) | ||
| + | assert self.n_layers > 0 | ||
| + | if not theano_rng: | ||
| + | theano_rng = MRG_RandomStreams(numpy_rng.randint(2 ** 30)) | ||
| + | # allocate symbolic variables for the data | ||
| + | # the data is presented as rasterized images | ||
| + | self.x = T.matrix('x') | ||
| + | # the labels are presented as 1D vector of [int] labels | ||
| + | self.y = T.ivector('y') | ||
| + | <code>self.sigmoid_layers</code> будет хранить графики прямой связи, которые вместе образуют MLP, в то время как <code>self.rbm_layers</code> будет хранить RBM, используемые для предварительной подготовки каждого уровня MLP. | ||
| + | Следующим шагом мы строим сигмоидные слои <code>n_layers</code> (мы используем класс <code>HiddenLayer</code>, введенный в Multilayer Perceptron, с единственной модификацией, в которой мы заменили нелинейность от <tex>tanh</tex> на логистическую функцию $s(x) = \frac{1}{1 + e^{-x}}$ и <code>n_layers</code> RBM, где <code>n_layers</code> {{---}} это глубина нашей модели. Мы связываем сигмоидные слои так, что они образуют MLP, и строим каждый RBM таким образом, чтобы они разделяли весовую матрицу и скрытое смещение с соответствующим сигмоидным слоем. | ||
| + | for i in range(self.n_layers): | ||
| + | if i == 0: | ||
| + | input_size = n_ins | ||
| + | else: | ||
| + | input_size = hidden_layers_sizes[i - 1] | ||
| + | if i == 0: | ||
| + | layer_input = self.x | ||
| + | else: | ||
| + | layer_input = self.sigmoid_layers[-1].output | ||
| + | sigmoid_layer = HiddenLayer(rng=numpy_rng, | ||
| + | input=layer_input, | ||
| + | n_in=input_size, | ||
| + | n_out=hidden_layers_sizes[i], | ||
| + | activation=T.nnet.sigmoid) | ||
| + | # add the layer to our list of layers | ||
| + | self.sigmoid_layers.append(sigmoid_layer) | ||
| + | self.params.extend(sigmoid_layer.params) | ||
| + | # Construct an RBM that shared weights with this layer | ||
| + | rbm_layer = RBM(numpy_rng=numpy_rng, | ||
| + | theano_rng=theano_rng, | ||
| + | input=layer_input, | ||
| + | n_visible=input_size, | ||
| + | n_hidden=hidden_layers_sizes[i], | ||
| + | W=sigmoid_layer.W, | ||
| + | hbias=sigmoid_layer.b) | ||
| + | self.rbm_layers.append(rbm_layer) | ||
| + | |||
| + | Осталось только сложить один последний уровень логистической регрессии, чтобы сформировать MLP. Мы будем использовать класс <code>LogisticRegression</code>: | ||
| + | self.logLayer = LogisticRegression(input=self.sigmoid_layers[-1].output, | ||
| + | n_in=hidden_layers_sizes[-1], | ||
| + | n_out=n_outs) | ||
| + | self.params.extend(self.logLayer.params) | ||
| + | self.finetune_cost = self.logLayer.negative_log_likelihood(self.y) | ||
| + | self.errors = self.logLayer.errors(self.y) | ||
| + | Класс также предоставляет метод, который генерирует обучающие функции для каждой из RBM. Они возвращаются в виде списка, где элемент <tex>i</tex> является функцией, которая реализует один этап обучения для RBM на уровне <tex>i</tex>. | ||
| + | def pretraining_functions(self, train_set_x, batch_size, k): | ||
| + | index = T.lscalar('index') # index to a minibatch | ||
| + | Чтобы иметь возможность изменять скорость обучения во время обучения, мы связываем с ней переменную <code>Theano</code>, которая имеет значение по умолчанию. | ||
| + | learning_rate = T.scalar('lr') # learning rate to use | ||
| + | # begining of a batch, given `index` | ||
| + | batch_begin = index * batch_size | ||
| + | # ending of a batch given `index` | ||
| + | batch_end = batch_begin + batch_size | ||
| + | pretrain_fns = [] | ||
| + | for rbm in self.rbm_layers: | ||
| + | # get the cost and the updates list | ||
| + | # using CD-k here (persisent=None) for training each RBM. | ||
| + | # TODO: change cost function to reconstruction error | ||
| + | cost, updates = rbm.get_cost_updates(learning_rate, persistent=None, k=k) | ||
| + | # compile the theano function | ||
| + | fn = theano.function( | ||
| + | inputs=[index, theano.In(learning_rate, value=0.1)], | ||
| + | outputs=cost, | ||
| + | updates=updates, | ||
| + | givens={ | ||
| + | self.x: train_set_x[batch_begin:batch_end] | ||
| + | } | ||
| + | ) | ||
| + | # append `fn` to the list of functions | ||
| + | pretrain_fns.append(fn) | ||
| + | return pretrain_fns | ||
| + | |||
| + | Теперь любая функция <code>pretrain_fns[i]</code> принимает в качестве аргумента индекс и, опционально, <code>lr</code> {{---}} скорость обучения. Обратите внимание, что имена параметров {{---}} это имена, данные переменным <code>Theano</code> (например, <code>lr</code>) при их создании, а не имена переменных python (например, <code>learning_rate</code>). Имейте это в виду при работе с <code>Theano</code>. При желании, если вы укажете <math>k</math> (количество шагов Гиббса, которые нужно выполнить на CD или PCD), это также станет аргументом функции. | ||
| + | |||
| + | Точно так же класс <code>DBN</code> включает метод для построения функций, необходимых для тонкой настройки (<code>train_model</code>, <code>validate_model</code> и <code>test_model</code>). | ||
| + | def build_finetune_functions(self, datasets, batch_size, learning_rate): | ||
| + | (train_set_x, train_set_y) = datasets[0] | ||
| + | (valid_set_x, valid_set_y) = datasets[1] | ||
| + | (test_set_x, test_set_y) = datasets[2] | ||
| + | # compute number of minibatches for training, validation and testing | ||
| + | n_valid_batches = valid_set_x.get_value(borrow=True).shape[0] | ||
| + | n_valid_batches //= batch_size | ||
| + | n_test_batches = test_set_x.get_value(borrow=True).shape[0] | ||
| + | n_test_batches //= batch_size | ||
| + | index = T.lscalar('index') # index to a [mini]batch | ||
| + | # compute the gradients with respect to the model parameters | ||
| + | gparams = T.grad(self.finetune_cost, self.params) | ||
| + | # compute list of fine-tuning updates | ||
| + | updates = [] | ||
| + | for param, gparam in zip(self.params, gparams): | ||
| + | updates.append((param, param - gparam * learning_rate)) | ||
| + | train_fn = theano.function( | ||
| + | inputs=[index], | ||
| + | outputs=self.finetune_cost, | ||
| + | updates=updates, | ||
| + | givens={ | ||
| + | self.x: train_set_x[ | ||
| + | index * batch_size: (index + 1) * batch_size | ||
| + | ], | ||
| + | self.y: train_set_y[ | ||
| + | index * batch_size: (index + 1) * batch_size | ||
| + | ] | ||
| + | } | ||
| + | ) | ||
| + | test_score_i = theano.function( | ||
| + | [index], | ||
| + | self.errors, | ||
| + | givens={ | ||
| + | self.x: test_set_x[ | ||
| + | index * batch_size: (index + 1) * batch_size | ||
| + | ], | ||
| + | self.y: test_set_y[ | ||
| + | index * batch_size: (index + 1) * batch_size | ||
| + | ] | ||
| + | } | ||
| + | ) | ||
| + | valid_score_i = theano.function( | ||
| + | [index], | ||
| + | self.errors, | ||
| + | givens={ | ||
| + | self.x: valid_set_x[ | ||
| + | index * batch_size: (index + 1) * batch_size | ||
| + | ], | ||
| + | self.y: valid_set_y[ | ||
| + | index * batch_size: (index + 1) * batch_size | ||
| + | ] | ||
| + | } | ||
| + | ) | ||
| + | # Create a function that scans the entire validation set | ||
| + | def valid_score(): | ||
| + | return [valid_score_i(i) for i in range(n_valid_batches)] | ||
| + | # Create a function that scans the entire test set | ||
| + | def test_score(): | ||
| + | return [test_score_i(i) for i in range(n_test_batches)] | ||
| + | return train_fn, valid_score, test_score | ||
| + | Обратите внимание, что возвращенные <code>valid_score</code> и <code>test_score</code> являются не функциями <code>Theano</code>, а скорее функциями Python. Они зацикливаются на всем наборе проверки и на всем наборе тестов, чтобы создать список потерь, полученных на этих наборах | ||
| + | |||
| + | В конце концов | ||
| + | несколько строк кода ниже создают глубокую сеть доверия: | ||
| + | numpy_rng = numpy.random.RandomState(123) | ||
| + | print('... building the model') | ||
| + | # construct the Deep Belief Network | ||
| + | dbn = DBN(numpy_rng=numpy_rng, n_ins=28 * 28, | ||
| + | hidden_layers_sizes=[1000, 1000, 1000], | ||
| + | n_outs=10) | ||
| + | Эта сеть состоит из двух этапов: (1) этап предварительного обучения и (2) этап точной настройки. | ||
| + | |||
| + | На этапе предварительного обучения мы перебираем все слои сети. Для каждого уровня мы используем скомпилированную функцию <code>anano</code>, которая определяет вход в RBM <tex>i</tex>-го уровня и выполняет один шаг CD-k в этом RBM. Эта функция применяется к обучающему набору для фиксированного числа эпох, заданных <code>pretraining_epochs</code>. | ||
| + | print('... getting the pretraining functions') | ||
| + | pretraining_fns = dbn.pretraining_functions(train_set_x=train_set_x, | ||
| + | batch_size=batch_size, | ||
| + | k=k) | ||
| + | print('... pre-training the model') | ||
| + | start_time = timeit.default_timer() | ||
| + | # Pre-train layer-wise | ||
| + | for i in range(dbn.n_layers): | ||
| + | # go through pretraining epochs | ||
| + | for epoch in range(pretraining_epochs): | ||
| + | # go through the training set | ||
| + | c = [] | ||
| + | for batch_index in range(n_train_batches): | ||
| + | c.append(pretraining_fns[i](index=batch_index, | ||
| + | lr=pretrain_lr)) | ||
| + | print('Pre-training layer %i, epoch %d, cost ' % (i, epoch), end=' ') | ||
| + | print(numpy.mean(c, dtype='float64')) | ||
| + | |||
| + | end_time = timeit.default_timer() | ||
| + | |||
| + | |||
| + | ==См. также== | ||
| + | *[[Глубокое обучение]] | ||
| + | *[[Метод опорных векторов (SVM)]] | ||
| + | |||
| + | == Примечания == | ||
| + | <references/> | ||
| + | ==Источники информации== | ||
| + | #[http://deeplearning.net/tutorial/DBN.html Статья Deeplearning о применении DBN] | ||
| + | #[https://en.wikipedia.org/wiki/Deep_belief_network wikipedia dbn] {{---}} Статья про DBN в Wikipedia | ||
| + | #[https://www.cs.toronto.edu/~hinton/nipstutorial/nipstut3.pdf 2007 NIPS Tutorial on: Deep Belief Nets] | ||
| + | #[https://pathmind.com/wiki/restricted-boltzmann-machine A Beginner's Guide to Restricted Boltzmann Machines] | ||
| + | |||
| + | [[Категория: Машинное обучение]] | ||
| + | [[Категория: Сети глубокого доверия]] | ||
Текущая версия на 19:30, 4 сентября 2022
Сети глубокого доверия — это вероятностные генеративные модели, которые состоят из нескольких слоев стохастических скрытых переменных. Скрытые переменные обычно имеют двоичные значения и часто называются скрытыми узлами или детекторами признаков. Два верхних слоя имеют ненаправленные, симметричные связи между ними и образуют ассоциативную память. Между оставшимися парами соседних слоёв есть только направленные связи от верхнего к нижнему. Состояния узлов в нижнем слое представляют вектор данных.
Два наиболее значимых свойства сетей глубокого доверия:
- Существует эффективная послойная процедура для обучения нисходящих весов, которая определяет, как переменные в одном слое зависят от переменных в слое выше.
- После обучения скрытых переменных в каждом слое могут быть выведены значения за один проход снизу вверх, который начинается с наблюдаемого вектора данных в нижнем слое и использует веса в обратном направлении.
Сети глубокого доверия обучаются по одному слою за раз, обрабатывая значения скрытых переменных в одном слое в тот момент, когда они выводятся из данных для обучения следующего слоя. Это эффективное, жадное обучение может сопровождаться или сочетаться с другими процедурами обучения, которые точно настраивают все веса для улучшения генеративных или дискриминационных характеристик всей сети.
Дискриминирующая тонкая настройка может быть выполнена путем добавления последнего слоя переменных, которые представляют желаемые выходные данные и производные ошибок обратного распространения. Когда сети со многими скрытыми слоями применяются к высокоструктурированным входным данным, таким как изображения, обратное распространение работает намного лучше, если детекторы признаков в скрытых слоях инициализируются путем обучения глубокой сети доверия, которая моделирует структуру во входных данных.
Содержание
Как развивались сети глубокого доверия
В нейронных сетях первого поколения использовались перцептроны, которые идентифицировали конкретный объект или что-либо еще, принимая во внимание «вес» или предварительные свойства. Однако перцептроны могут быть эффективны только на базовом уровне и бесполезны для передовых технологий. Для решения этих проблем во втором поколении нейронных сетей была введена концепция обратного распространения, при которой полученный вывод сравнивается с желаемым выводом, а значение ошибки было снижено до нуля. Метод опорных векторов позволил создать больше контрольных примеров, ссылаясь на ранее введенные контрольные примеры. Затем последовали циклические графы, называемые сетями доверия, которые помогли в решении проблем, связанных с выводом и проблемами обучения. За этим последовали сети глубокого доверия, которые помогли создать непредвзятые значения для хранения в конечных узлах.
Композиция простых обучающих модулей
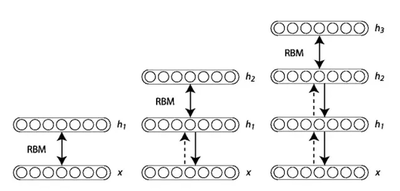
Глубокая сеть доверия может рассматриваться как набор простых обучающих модулей, каждый из которых представляет собой ограниченную машину Больцмана[1], которая содержит слой видимых узлов, представляющий данные, и слой скрытых узлов, которые обучаются представлению особенностей, которые захватывают более высокие порядки корреляции в данных. Ограниченные машины Больцмана могут быть сложены и обучены жадным алгоритмом, чтобы сформировать так называемые глубокие сети доверия, которые моделируют совместное распределение между наблюдаемым вектором и скрытыми слоями следующим образом:
где $x=h^0$, $P(h^{k-1}|h^{k})$ — условное распределение для видимых узлов, обусловленных скрытыми узлами RBM на уровне , и $P(h^{l - 1}|h^l)$ — это видимое-скрытое совместное распределение в RBM верхнего уровня. Это показано на рисунке 1.
Ограниченная машина Больцмана (RBM)
Если вы знаете, что такое факторный анализ, то RBM можно рассматривать как двоичную версию факторного анализа. Таким образом, вместо множества факторов, определяющих вывод, мы можем иметь двоичную переменную в форме 0 или 1.
Например: если вы читаете книгу, а затем судите эту книгу по двухзначной шкале: это либо вам нравится книга, либо вам не нравится книга. В таких сценариях мы можем использовать RBM, которые помогут нам определить причину, по которой мы делаем такой выбор.
RBM используют вероятностный подход для нейронных сетей, и поэтому их также называют стохастическими нейронными сетями. Если мы разложим RBM, то становится ясно, что они состоят из трех частей:
- Один входной слой, так называемые "Видимые узлы".
- Один скрытый слой.
- Узлы смещения.
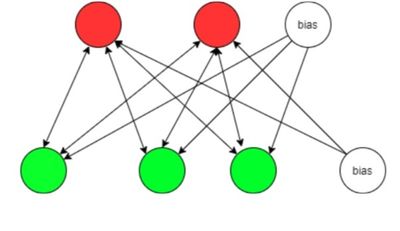
В приведенном выше примере видимые узлы — это не что иное, как то, нравится ли вам книга или нет. Скрытые узлы помогают найти то, что заставило вас одобрить эту книгу. Узлы смещения добавлены, чтобы включить различные виды свойств, разных книг. Простая визуализация Ограниченной машины Больцмана показана на рисунке 2.
Зеленым отмечены видимые узлы, красным скрытые, а белые узлы с меткой "bias" соответствуют узлам смещения.
Сети глубокого доверия имеют две фазы:
- Фаза предварительного обучения.
- Фаза тонкой настройки.
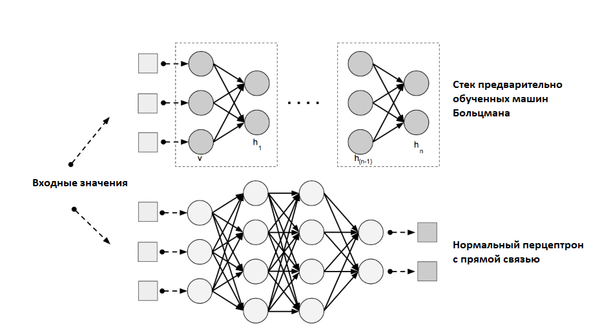
Фаза предварительного обучения — это не что иное, как несколько уровней RBN, в то время как фаза тонкой настройки — это нейронная сеть с прямой связью. Визуализация обеих фаз показана на рисунке 3 ниже
Алгоритм обучения глубокой сети доверия, состоит из нескольких этапов:
- Нахождение признаков видимых узлов, используя алгоритм контрастной дивергенции.
- Нахождение скрытых признаков объектов, найденных в предыдущем шаге.
Реализация
Мы начнем с определения класса для глубокой сети доверия, который назовем DBN (Deep belief network), который будет хранить уровни многослойного перцептрона MLP (Multilayer perceptron) вместе со связанными с ними RBM. Поскольку мы используем RBM для инициализации MLP, код будет отражать эту идею, насколько это возможно. Далее будут приведены RBM, используемые для инициализации сети, и MLP, используемый для классификации.
from __future__ import print_function, division import os import sys import timeit import numpy import theano import theano.tensor as T
from theano.sandbox.rng_mrg import MRG_RandomStreams from logistic_sgd import LogisticRegression, load_data from mlp import HiddenLayer from rbm import RBM
class DBN(object):
def __init__(self, numpy_rng, theano_rng=None, n_ins=784, hidden_layers_sizes=[500, 500], n_outs=10):
self.sigmoid_layers = []
self.rbm_layers = []
self.params = []
self.n_layers = len(hidden_layers_sizes)
assert self.n_layers > 0
if not theano_rng:
theano_rng = MRG_RandomStreams(numpy_rng.randint(2 ** 30))
# allocate symbolic variables for the data
# the data is presented as rasterized images
self.x = T.matrix('x')
# the labels are presented as 1D vector of [int] labels
self.y = T.ivector('y')
self.sigmoid_layers будет хранить графики прямой связи, которые вместе образуют MLP, в то время как self.rbm_layers будет хранить RBM, используемые для предварительной подготовки каждого уровня MLP.
Следующим шагом мы строим сигмоидные слои n_layers (мы используем класс HiddenLayer, введенный в Multilayer Perceptron, с единственной модификацией, в которой мы заменили нелинейность от на логистическую функцию $s(x) = \frac{1}{1 + e^{-x}}$ и n_layers RBM, где n_layers — это глубина нашей модели. Мы связываем сигмоидные слои так, что они образуют MLP, и строим каждый RBM таким образом, чтобы они разделяли весовую матрицу и скрытое смещение с соответствующим сигмоидным слоем.
for i in range(self.n_layers):
if i == 0:
input_size = n_ins
else:
input_size = hidden_layers_sizes[i - 1]
if i == 0:
layer_input = self.x
else:
layer_input = self.sigmoid_layers[-1].output
sigmoid_layer = HiddenLayer(rng=numpy_rng,
input=layer_input,
n_in=input_size,
n_out=hidden_layers_sizes[i],
activation=T.nnet.sigmoid)
# add the layer to our list of layers
self.sigmoid_layers.append(sigmoid_layer)
self.params.extend(sigmoid_layer.params)
# Construct an RBM that shared weights with this layer
rbm_layer = RBM(numpy_rng=numpy_rng,
theano_rng=theano_rng,
input=layer_input,
n_visible=input_size,
n_hidden=hidden_layers_sizes[i],
W=sigmoid_layer.W,
hbias=sigmoid_layer.b)
self.rbm_layers.append(rbm_layer)
Осталось только сложить один последний уровень логистической регрессии, чтобы сформировать MLP. Мы будем использовать класс LogisticRegression:
self.logLayer = LogisticRegression(input=self.sigmoid_layers[-1].output,
n_in=hidden_layers_sizes[-1],
n_out=n_outs)
self.params.extend(self.logLayer.params)
self.finetune_cost = self.logLayer.negative_log_likelihood(self.y)
self.errors = self.logLayer.errors(self.y)
Класс также предоставляет метод, который генерирует обучающие функции для каждой из RBM. Они возвращаются в виде списка, где элемент является функцией, которая реализует один этап обучения для RBM на уровне .
def pretraining_functions(self, train_set_x, batch_size, k):
index = T.lscalar('index') # index to a minibatch
Чтобы иметь возможность изменять скорость обучения во время обучения, мы связываем с ней переменную Theano, которая имеет значение по умолчанию.
learning_rate = T.scalar('lr') # learning rate to use
# begining of a batch, given `index`
batch_begin = index * batch_size
# ending of a batch given `index`
batch_end = batch_begin + batch_size
pretrain_fns = []
for rbm in self.rbm_layers:
# get the cost and the updates list
# using CD-k here (persisent=None) for training each RBM.
# TODO: change cost function to reconstruction error
cost, updates = rbm.get_cost_updates(learning_rate, persistent=None, k=k)
# compile the theano function
fn = theano.function(
inputs=[index, theano.In(learning_rate, value=0.1)],
outputs=cost,
updates=updates,
givens={
self.x: train_set_x[batch_begin:batch_end]
}
)
# append `fn` to the list of functions
pretrain_fns.append(fn)
return pretrain_fns
Теперь любая функция pretrain_fns[i] принимает в качестве аргумента индекс и, опционально, lr — скорость обучения. Обратите внимание, что имена параметров — это имена, данные переменным Theano (например, lr) при их создании, а не имена переменных python (например, learning_rate). Имейте это в виду при работе с Theano. При желании, если вы укажете (количество шагов Гиббса, которые нужно выполнить на CD или PCD), это также станет аргументом функции.
Точно так же класс DBN включает метод для построения функций, необходимых для тонкой настройки (train_model, validate_model и test_model).
def build_finetune_functions(self, datasets, batch_size, learning_rate):
(train_set_x, train_set_y) = datasets[0]
(valid_set_x, valid_set_y) = datasets[1]
(test_set_x, test_set_y) = datasets[2]
# compute number of minibatches for training, validation and testing
n_valid_batches = valid_set_x.get_value(borrow=True).shape[0]
n_valid_batches //= batch_size
n_test_batches = test_set_x.get_value(borrow=True).shape[0]
n_test_batches //= batch_size
index = T.lscalar('index') # index to a [mini]batch
# compute the gradients with respect to the model parameters
gparams = T.grad(self.finetune_cost, self.params)
# compute list of fine-tuning updates
updates = []
for param, gparam in zip(self.params, gparams):
updates.append((param, param - gparam * learning_rate))
train_fn = theano.function(
inputs=[index],
outputs=self.finetune_cost,
updates=updates,
givens={
self.x: train_set_x[
index * batch_size: (index + 1) * batch_size
],
self.y: train_set_y[
index * batch_size: (index + 1) * batch_size
]
}
)
test_score_i = theano.function(
[index],
self.errors,
givens={
self.x: test_set_x[
index * batch_size: (index + 1) * batch_size
],
self.y: test_set_y[
index * batch_size: (index + 1) * batch_size
]
}
)
valid_score_i = theano.function(
[index],
self.errors,
givens={
self.x: valid_set_x[
index * batch_size: (index + 1) * batch_size
],
self.y: valid_set_y[
index * batch_size: (index + 1) * batch_size
]
}
)
# Create a function that scans the entire validation set
def valid_score():
return [valid_score_i(i) for i in range(n_valid_batches)]
# Create a function that scans the entire test set
def test_score():
return [test_score_i(i) for i in range(n_test_batches)]
return train_fn, valid_score, test_score
Обратите внимание, что возвращенные valid_score и test_score являются не функциями Theano, а скорее функциями Python. Они зацикливаются на всем наборе проверки и на всем наборе тестов, чтобы создать список потерь, полученных на этих наборах
В конце концов несколько строк кода ниже создают глубокую сеть доверия:
numpy_rng = numpy.random.RandomState(123)
print('... building the model')
# construct the Deep Belief Network
dbn = DBN(numpy_rng=numpy_rng, n_ins=28 * 28,
hidden_layers_sizes=[1000, 1000, 1000],
n_outs=10)
Эта сеть состоит из двух этапов: (1) этап предварительного обучения и (2) этап точной настройки.
На этапе предварительного обучения мы перебираем все слои сети. Для каждого уровня мы используем скомпилированную функцию anano, которая определяет вход в RBM -го уровня и выполняет один шаг CD-k в этом RBM. Эта функция применяется к обучающему набору для фиксированного числа эпох, заданных pretraining_epochs.
print('... getting the pretraining functions')
pretraining_fns = dbn.pretraining_functions(train_set_x=train_set_x,
batch_size=batch_size,
k=k)
print('... pre-training the model')
start_time = timeit.default_timer()
# Pre-train layer-wise
for i in range(dbn.n_layers):
# go through pretraining epochs
for epoch in range(pretraining_epochs):
# go through the training set
c = []
for batch_index in range(n_train_batches):
c.append(pretraining_fns[i](index=batch_index,
lr=pretrain_lr))
print('Pre-training layer %i, epoch %d, cost ' % (i, epoch), end=' ')
print(numpy.mean(c, dtype='float64'))
end_time = timeit.default_timer()