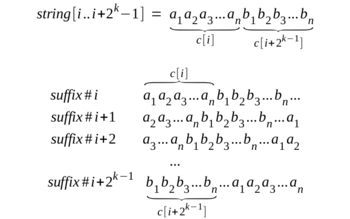Алгоритм цифровой сортировки суффиксов циклической строки — различия между версиями
(→Решение) |
м (rollbackEdits.php mass rollback) |
||
| (не показано 45 промежуточных версий 11 участников) | |||
| Строка 1: | Строка 1: | ||
| − | {{ | + | {{Задача |
| + | |definition = Дана циклическая строка <tex>s[0 .. n - 1]</tex>. Суффиксом циклической строки <tex>s</tex> называется строка <tex>s[i .. n - 1] + s[0 .. i - 1], i < n </tex> (будем называть такую строку суффиксом под номером <tex>i</tex>). Требуется отсортировать все её суффиксы в порядке лексикографической сортировки. | ||
| + | }} | ||
| − | == | + | == Решение == |
| + | Рассматриваемый алгоритм состоит из <tex>\lceil\log n\rceil + 1</tex> итераций. На <tex>k</tex>-той итерации (<tex>k=0..\lceil\log n\rceil </tex>) сортируются циклические подстроки длины <tex>2^k</tex>. На последней, <tex>\lceil\log n\rceil</tex>-ой итерации, будут сортироваться подстроки длины <tex>2^{\lceil\log n\rceil} \geqslant n</tex>, что эквивалентно сортировке циклических сдвигов. | ||
| + | |||
| + | На каждой итерации будем хранить массив перестановки <tex>p[0 .. n - 1]</tex>, где <tex>p[i]</tex> — номер суффикса, занимающего позицию <tex>i</tex> в текущей перестановке. Также будем хранить массив классов эквивалентности <tex>c[0 .. n - 1]</tex>, где <tex>c[i]</tex> — класс эквивалентности, которому принадлежит префикс длины <tex>2^k</tex> суффикса под номером <tex>p[i]</tex>. При этом если префикс суффикса под номером <tex>p[i]</tex> лексикографически меньше префикса суффикса под номером <tex>p[j]</tex>, то <tex>c[i] < c[j]</tex>. Если же префиксы равны, то и их классы эквивалентности одинаковы. Так как мы вставили в строку символ <tex>\$</tex>, то к концу алгоритма каждый суффикс будет иметь уникальный класс эквивалентности, значит, мы установим порядок суффиксов. | ||
| + | |||
| + | == Описание алгоритма == | ||
| − | + | На нулевой итерации отсортируем циклические подстроки длины <tex>1</tex>, т.е. первые символы строк, и разделим их на классы эквивалентности (одинаковые символы должны быть отнесены к одному классу эквивалентности). При помощи [[Сортировка подсчетом|сортировки подсчетом]] построим массив <tex>p</tex>, содержащий номера суффиксов, отсортированных в лексикографическом порядке. По этому массиву построим массив классов эквивалентности <tex>c</tex>. | |
| − | + | На <tex>k</tex>-ом проходе имеем массивы <tex>p</tex> и <tex>c</tex>, вычисленные на предыдущей итерации. Приведем алгоритм, выполняющий <tex>k</tex>-ый проход за <tex>O(n)</tex>. Поскольку итераций всего <tex>O(\log n)</tex>, такой алгоритм имеет асимптотику <tex>O(n \log n)</tex>. | |
| − | + | ||
| + | Заметим, что циклическая подстрока длины <tex>2^k</tex> состоит из двух подстрок длины <tex>2^{k-1}</tex>, которые мы можем сравнивать между собой за <tex>O(1)</tex>, используя информацию с предыдущей итерации — номера классов эквивалентности <tex>c</tex>. Таким образом, для подстроки длины <tex>2^k</tex>, начинающейся в позиции <tex>i</tex>, вся необходимая информация содержится в паре чисел <tex>\langle c[i], c[i + 2^{k-1}]\rangle </tex>. | ||
| − | + | [[Файл:Suff_array.png|350px|thumb|right|Циклическая подстрока длины <tex>2^k</tex> и порядок ее частей с прерыдущей итерации.]] | |
| − | + | Отсортируем подстроки длины <tex>2^k</tex> по данным парам и запишем порядок в массив <tex>p</tex>. Воспользуемся здесь приёмом, на котором основана [[Цифровая сортировка| цифровая сортировка]]: отсортируем пары сначала по вторым элементам, а затем по первым (устойчивой сортировкой). Однако вторые элементы уже упорядочены — этот порядок задан в массиве от предыдущей итерации. Тогда, чтобы получить порядок пар по вторым элементам, надо от каждого элемента массива <tex>p</tex> отнять <tex>2^{k-1}</tex> (<tex>p</tex> даёт упорядочение подстрок длины <tex>2^{k-1}</tex>, и при переходе к строке вдвое большей длины эти подстроки становятся их вторыми половинками, поэтому от позиции второй половинки отнимается длина первой половинки). | |
| − | + | Чтобы произвести устойчивую сортировку по первым элементам пар, воспользуемся сортировкой подсчетом, имеющую асимптотику <tex>O(n)</tex>. | |
| − | + | Осталось пересчитать номера классов эквивалентности <tex>c</tex>, пройдя по новой перестановке <tex>p</tex> и сравнивая соседние элементы (как пары двух чисел). | |
| − | + | ==Пример== | |
| + | <tex> | ||
| + | s = abacaba\$ \\ | ||
| + | i' = i + 2^{k-1} \\ | ||
| + | </tex> | ||
| + | {| class="wikitable" style="text-align: center;" | ||
| + | ! colspan="3" | 0 фаза | ||
| + | ! colspan="4" | 1 фаза | ||
| + | ! colspan="4" | 2 фаза | ||
| + | ! colspan="4" | 3 фаза | ||
| + | |- | ||
| + | | p | ||
| + | | s | ||
| + | | c | ||
| + | | p | ||
| + | | | ||
| + | | | ||
| + | | c | ||
| + | | p | ||
| + | | | ||
| + | | | ||
| + | | c | ||
| + | | p | ||
| + | | | ||
| + | | | ||
| + | | c | ||
| + | |- | ||
| + | | 7 | ||
| + | | $ | ||
| + | | 1 | ||
| + | | 7 | ||
| + | | $a | ||
| + | | 1,2 | ||
| + | | 1 | ||
| + | | 7 | ||
| + | | $aba | ||
| + | | 1,5 | ||
| + | | 1 | ||
| + | | 7 | ||
| + | | $abacaba | ||
| + | | 1,8 | ||
| + | | 1 | ||
| + | |- | ||
| + | | 0 | ||
| + | | a | ||
| + | | 2 | ||
| + | | 6 | ||
| + | | a$ | ||
| + | | 2,1 | ||
| + | | 2 | ||
| + | | 6 | ||
| + | | a$ab | ||
| + | | 2,3 | ||
| + | | 2 | ||
| + | | 6 | ||
| + | | a$abacab | ||
| + | | 2,5 | ||
| + | | 2 | ||
| + | |- | ||
| + | | 2 | ||
| + | | a | ||
| + | | 2 | ||
| + | | 0 | ||
| + | | ab | ||
| + | | 2,3 | ||
| + | | 3 | ||
| + | | 4 | ||
| + | | aba$ | ||
| + | | 3,2 | ||
| + | | 3 | ||
| + | | 4 | ||
| + | | aba$abac | ||
| + | | 3,4 | ||
| + | | 3 | ||
| + | |- | ||
| + | | 4 | ||
| + | | a | ||
| + | | 2 | ||
| + | | 4 | ||
| + | | ab | ||
| + | | 2,3 | ||
| + | | 3 | ||
| + | | 0 | ||
| + | | abac | ||
| + | | 3,4 | ||
| + | | 4 | ||
| + | | 0 | ||
| + | | abacaba$ | ||
| + | | 4,3 | ||
| + | | 4 | ||
| + | |- | ||
| + | | 6 | ||
| + | | a | ||
| + | | 2 | ||
| + | | 2 | ||
| + | | ac | ||
| + | | 2,4 | ||
| + | | 4 | ||
| + | | 2 | ||
| + | | acab | ||
| + | | 4,3 | ||
| + | | 5 | ||
| + | | 2 | ||
| + | | acaba$ab | ||
| + | | 5,2 | ||
| + | | 5 | ||
| + | |- | ||
| + | | 1 | ||
| + | | b | ||
| + | | 3 | ||
| + | | 1 | ||
| + | | ba | ||
| + | | 3,1 | ||
| + | | 5 | ||
| + | | 5 | ||
| + | | ba$a | ||
| + | | 5,1 | ||
| + | | 6 | ||
| + | | 5 | ||
| + | | ba$abaca | ||
| + | | 6,7 | ||
| + | | 6 | ||
| + | |- | ||
| + | | 5 | ||
| + | | b | ||
| + | | 3 | ||
| + | | 5 | ||
| + | | ba | ||
| + | | 3,1 | ||
| + | | 5 | ||
| + | | 1 | ||
| + | | baca | ||
| + | | 5,6 | ||
| + | | 7 | ||
| + | | 1 | ||
| + | | bacaba$a | ||
| + | | 7,6 | ||
| + | | 7 | ||
| + | |- | ||
| + | | 3 | ||
| + | | c | ||
| + | | 4 | ||
| + | | 3 | ||
| + | | ca | ||
| + | | 4,1 | ||
| + | | 6 | ||
| + | | 3 | ||
| + | | caba | ||
| + | | 6,5 | ||
| + | | 8 | ||
| + | | 3 | ||
| + | | caba$aba | ||
| + | | 8,1 | ||
| + | | 8 | ||
| + | |} | ||
| − | + | ==Псевдокод== | |
| + | <font color=darkgreen>/* преобразует масив count, так что | ||
| + | теперь он содержит позиции в массиве suffs с которых | ||
| + | необходимо вставлять подстроки, начинающиеся с соответствующих символов */</font> | ||
| + | '''int[]''' calc_positions('''int[]''' count) | ||
| + | count[0] = 0 | ||
| + | '''for''' i = 2 .. count.length - 1 | ||
| + | count[i] += count[i - 1] | ||
| + | '''return''' count | ||
| + | |||
| + | <font color=darkgreen>/* принимает строку, для которой требуется построить суффиксный массив | ||
| + | возвращает суффиксный массив */</font> | ||
| + | '''int[]''' suff_array('''string''' str) | ||
| + | s += '$' | ||
| + | |||
| + | <font color=darkgreen>// нулевая итерация</font> | ||
| + | count = '''int'''[max(<tex>|\Sigma|</tex>, str.length)] | ||
| + | '''fill'''(count, 0) | ||
| + | '''for''' ch '''in''' str | ||
| + | count[ch]++ | ||
| + | count = '''calc_positions'''(count) | ||
| + | <font color=darkgreen>// suffs будет хранить индексы начал отсортированных подстрок текущей длины</font> | ||
| + | suffs = '''int'''[str.length] | ||
| + | '''for''' ch '''in''' str | ||
| + | suffs[count[ch]++] = i | ||
| + | classes = '''int'''[str.length] | ||
| + | classesN = 0 | ||
| + | last_char = '$' | ||
| + | '''for''' suf '''in''' suffs | ||
| + | '''if''' s[suf] <tex> \neq </tex> last_char | ||
| + | last_char = s[suf[i]] | ||
| + | classesN++ | ||
| + | classes[suf] = classesN | ||
| + | |||
| + | <font color=darkgreen>// нулевая итерация завершена | ||
| + | // сортируем подстроки длиной 2 * cur_len = 2^k</font> | ||
| + | cur_len = 1 | ||
| + | '''while''' cur_len <tex> \leqslant </tex> str.length | ||
| + | <font color=darkgreen>// сортируем по второй половине подстроки</font> | ||
| + | sorted_by2 = '''int'''[str.length] | ||
| + | '''for''' i = 0 .. str.length - 1 | ||
| + | sorted_by2[i] = (suffs[i] + str.length - cur_len) '''mod''' str.length | ||
| + | <font color=darkgreen>// сортируем по первой половине | ||
| + | // сортировка устойчивая, значит получим целиком отсортированные подстроки</font> | ||
| + | '''fill'''(count, 0) | ||
| + | '''for''' by2 '''in''' sorted_by2 | ||
| + | count[classes[by2]]++ | ||
| + | count = '''calc_positions'''(count) | ||
| + | '''for''' i = 0 .. str.length - 1 | ||
| + | suffs[count[classes[sorted_by2[i]]]++] = sorted_by2[i] | ||
| + | |||
| + | new_classes = '''int'''[str.length] | ||
| + | classesN = 0 | ||
| + | '''for''' i = 0 .. str.length - 1 | ||
| + | mid1 = (suffs[i] + cur_len) '''mod''' str.length | ||
| + | mid2 = (suffs[i - 1] + cur_len) '''mod''' str.length | ||
| + | '''if''' classes[suffs[i]] <tex> \neq </tex> classes[suffs[i-1]] '''or''' classes[mid1] <tex> \neq </tex> classes[mid2] | ||
| + | classesN++ | ||
| + | new_classes[suffs[i]] = classesN | ||
| + | classes = new_classes | ||
| + | cur_len *= 2 | ||
| + | '''return''' suffs | ||
| − | + | == См. также == | |
| + | * [[Суффиксный массив]] | ||
| + | * [[Построение суффиксного массива с помощью стандартных методов сортировки]] | ||
| − | + | == Источники информации == | |
| + | * [http://e-maxx.ru/algo/suffix_array MAXimal :: algo :: Суффиксный массив] | ||
| + | * [http://www.geeksforgeeks.org/suffix-array-set-2-a-nlognlogn-algorithm Suffix Array | Set 2 (nLogn Algorithm)] | ||
| − | + | [[Категория: Алгоритмы и структуры данных]] | |
| + | [[Категория: Суффиксный массив]] | ||
| + | [[Категория: Структуры данных]] | ||
Текущая версия на 19:30, 4 сентября 2022
| Задача: |
| Дана циклическая строка . Суффиксом циклической строки называется строка (будем называть такую строку суффиксом под номером ). Требуется отсортировать все её суффиксы в порядке лексикографической сортировки. |
Решение
Рассматриваемый алгоритм состоит из итераций. На -той итерации () сортируются циклические подстроки длины . На последней, -ой итерации, будут сортироваться подстроки длины , что эквивалентно сортировке циклических сдвигов.
На каждой итерации будем хранить массив перестановки , где — номер суффикса, занимающего позицию в текущей перестановке. Также будем хранить массив классов эквивалентности , где — класс эквивалентности, которому принадлежит префикс длины суффикса под номером . При этом если префикс суффикса под номером лексикографически меньше префикса суффикса под номером , то . Если же префиксы равны, то и их классы эквивалентности одинаковы. Так как мы вставили в строку символ , то к концу алгоритма каждый суффикс будет иметь уникальный класс эквивалентности, значит, мы установим порядок суффиксов.
Описание алгоритма
На нулевой итерации отсортируем циклические подстроки длины , т.е. первые символы строк, и разделим их на классы эквивалентности (одинаковые символы должны быть отнесены к одному классу эквивалентности). При помощи сортировки подсчетом построим массив , содержащий номера суффиксов, отсортированных в лексикографическом порядке. По этому массиву построим массив классов эквивалентности .
На -ом проходе имеем массивы и , вычисленные на предыдущей итерации. Приведем алгоритм, выполняющий -ый проход за . Поскольку итераций всего , такой алгоритм имеет асимптотику .
Заметим, что циклическая подстрока длины состоит из двух подстрок длины , которые мы можем сравнивать между собой за , используя информацию с предыдущей итерации — номера классов эквивалентности . Таким образом, для подстроки длины , начинающейся в позиции , вся необходимая информация содержится в паре чисел .
Отсортируем подстроки длины по данным парам и запишем порядок в массив . Воспользуемся здесь приёмом, на котором основана цифровая сортировка: отсортируем пары сначала по вторым элементам, а затем по первым (устойчивой сортировкой). Однако вторые элементы уже упорядочены — этот порядок задан в массиве от предыдущей итерации. Тогда, чтобы получить порядок пар по вторым элементам, надо от каждого элемента массива отнять ( даёт упорядочение подстрок длины , и при переходе к строке вдвое большей длины эти подстроки становятся их вторыми половинками, поэтому от позиции второй половинки отнимается длина первой половинки).
Чтобы произвести устойчивую сортировку по первым элементам пар, воспользуемся сортировкой подсчетом, имеющую асимптотику .
Осталось пересчитать номера классов эквивалентности , пройдя по новой перестановке и сравнивая соседние элементы (как пары двух чисел).
Пример
| 0 фаза | 1 фаза | 2 фаза | 3 фаза | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| p | s | c | p | c | p | c | p | c | ||||||
| 7 | $ | 1 | 7 | $a | 1,2 | 1 | 7 | $aba | 1,5 | 1 | 7 | $abacaba | 1,8 | 1 |
| 0 | a | 2 | 6 | a$ | 2,1 | 2 | 6 | a$ab | 2,3 | 2 | 6 | a$abacab | 2,5 | 2 |
| 2 | a | 2 | 0 | ab | 2,3 | 3 | 4 | aba$ | 3,2 | 3 | 4 | aba$abac | 3,4 | 3 |
| 4 | a | 2 | 4 | ab | 2,3 | 3 | 0 | abac | 3,4 | 4 | 0 | abacaba$ | 4,3 | 4 |
| 6 | a | 2 | 2 | ac | 2,4 | 4 | 2 | acab | 4,3 | 5 | 2 | acaba$ab | 5,2 | 5 |
| 1 | b | 3 | 1 | ba | 3,1 | 5 | 5 | ba$a | 5,1 | 6 | 5 | ba$abaca | 6,7 | 6 |
| 5 | b | 3 | 5 | ba | 3,1 | 5 | 1 | baca | 5,6 | 7 | 1 | bacaba$a | 7,6 | 7 |
| 3 | c | 4 | 3 | ca | 4,1 | 6 | 3 | caba | 6,5 | 8 | 3 | caba$aba | 8,1 | 8 |
Псевдокод
/* преобразует масив count, так что
теперь он содержит позиции в массиве suffs с которых
необходимо вставлять подстроки, начинающиеся с соответствующих символов */
int[] calc_positions(int[] count)
count[0] = 0
for i = 2 .. count.length - 1
count[i] += count[i - 1]
return count
/* принимает строку, для которой требуется построить суффиксный массив
возвращает суффиксный массив */
int[] suff_array(string str)
s += '$'
// нулевая итерация
count = int[max(, str.length)]
fill(count, 0)
for ch in str
count[ch]++
count = calc_positions(count)
// suffs будет хранить индексы начал отсортированных подстрок текущей длины
suffs = int[str.length]
for ch in str
suffs[count[ch]++] = i
classes = int[str.length]
classesN = 0
last_char = '$'
for suf in suffs
if s[suf] last_char
last_char = s[suf[i]]
classesN++
classes[suf] = classesN
// нулевая итерация завершена
// сортируем подстроки длиной 2 * cur_len = 2^k
cur_len = 1
while cur_len str.length
// сортируем по второй половине подстроки
sorted_by2 = int[str.length]
for i = 0 .. str.length - 1
sorted_by2[i] = (suffs[i] + str.length - cur_len) mod str.length
// сортируем по первой половине
// сортировка устойчивая, значит получим целиком отсортированные подстроки
fill(count, 0)
for by2 in sorted_by2
count[classes[by2]]++
count = calc_positions(count)
for i = 0 .. str.length - 1
suffs[count[classes[sorted_by2[i]]]++] = sorted_by2[i]
new_classes = int[str.length]
classesN = 0
for i = 0 .. str.length - 1
mid1 = (suffs[i] + cur_len) mod str.length
mid2 = (suffs[i - 1] + cur_len) mod str.length
if classes[suffs[i]] classes[suffs[i-1]] or classes[mid1] classes[mid2]
classesN++
new_classes[suffs[i]] = classesN
classes = new_classes
cur_len *= 2
return suffs