Символ Похгаммера — различия между версиями
м (rollbackEdits.php mass rollback) |
|||
| (не показаны 44 промежуточные версии 4 участников) | |||
| Строка 1: | Строка 1: | ||
| − | + | {{Определение | |
| − | + | |definition= | |
В математике '''убывающим факториалом''' (англ. ''falling factorial'') (иногда называется '''нисходящим факториалом''', '''постепенно убывающим факториалом''' или '''нижним факториалом''') обозначают: | В математике '''убывающим факториалом''' (англ. ''falling factorial'') (иногда называется '''нисходящим факториалом''', '''постепенно убывающим факториалом''' или '''нижним факториалом''') обозначают: | ||
| − | + | :<tex>(x)_{n}=x^{\underline{n}}=x(x-1)(x-2)\cdots(x-n+1)=\prod\limits_{k=1}^{n}(x-(k-1))=\prod\limits_{k=0}^{n-1}(x-k)</tex> | |
| − | :<tex>(x)_{n}=x^{\underline{n}}=x(x-1)(x-2)\cdots(x-n+1)=\ | + | При <tex>n=0</tex> значение принимается равным <tex>1</tex> (пустое произведение). |
| − | + | }} | |
| + | {{Определение | ||
| + | |definition= | ||
'''Растущий факториал''' (англ. ''rising factorial'') (иногда называется '''функцией Похгаммера''', '''многочленом Похгаммера''', '''восходящим факториалом''', '''постепенно растущим произведением''' или '''верхним факториалом''') определяется следующей формулой: | '''Растущий факториал''' (англ. ''rising factorial'') (иногда называется '''функцией Похгаммера''', '''многочленом Похгаммера''', '''восходящим факториалом''', '''постепенно растущим произведением''' или '''верхним факториалом''') определяется следующей формулой: | ||
| + | :<tex>x^{(n)}=x^{\overline{n}}=x(x+1)(x+2)\cdots(x+n-1)=\prod\limits_{k=1}^{n}(x+(k-1))=\prod\limits_{k=0}^{n-1}(x+k). </tex> | ||
| + | При <tex>n=0</tex> значение принимается равным <tex>1</tex> (пустое произведение). | ||
| + | }} | ||
| − | + | Грахам, Кнут и Паташник<ref>Ronald L. Graham, Donald E. Knuth and Oren Patashnik in their book ''Concrete Mathematics'' (<tex>1988</tex>), Addison-Wesley, Reading MA. ISBN <tex>0-201-14236-8</tex>, pp. <tex>47</tex>,<tex>48</tex></ref> предложили произносить эти записи как "<tex>x</tex> растущий к <tex>m</tex>" и "<tex>x</tex> убывающий к <tex>m</tex>" соответственно. | |
| − | + | В зависимости от контекста символ Похгаммера может обозначать как растущий факториал, так и убывающий факториал. | |
| − | + | Когда <tex>x</tex> неотрицательное целое число, <tex>(x)_n</tex> равняется числу инъективных отображений<ref name="Injective function">[https://en.wikipedia.org/wiki/Injective_function Injective function]</ref> из множества с <tex>n</tex> элементами во множество из <tex>x</tex> элементов. Для обозначения этого числа часто применяют обозначения <tex>_x P_n</tex> и <tex>P(x,n)</tex>. Символ Похгаммера в основном используется в алгебре, где <tex>x</tex> {{---}} переменная, то есть <tex>(x)_n</tex> есть ни что иное как многочлен степени <tex>n</tex> от <tex>x</tex>. | |
| − | + | <b>Замечание</b> | |
| − | + | Другие формы записи убывающего факториала: <tex>P(x,n)</tex>, <tex>^x P_n</tex>, ,<tex>P_{x,n}</tex> или <tex>_x P_n</tex>. | |
| + | Другое обозначение растущего факториала <tex>x^{(n)}</tex> реже встречается, чем <tex>(x)^+_n</tex>. Обозначение <tex>(x)^+_n</tex> используется для растущего факториала, запись <tex>(x)^-_n</tex> обычно применяется для обозначения убывающего факториала для избежания недоразумений.<ref name=Knuth>According to Knuth, The Art of Computer Programming, Vol. <tex>1</tex>, <tex>3</tex>rd ed., p. <tex>50</tex>.</ref> | ||
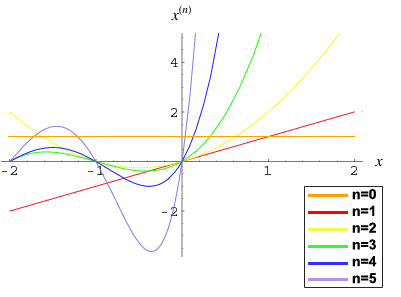
| + | [[File:RisingFactorial_3.jpg|401px|thumb|upright|График растущего факториала для <tex>n</tex> от <tex>0</tex> до <tex>4</tex>]] | ||
==Примеры== | ==Примеры== | ||
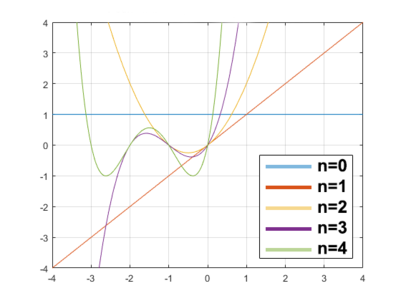
| + | [[File:PlotThePochhammerSymbolExample_02.png|401px|thumb|upright|График убывающего факториала для <tex>n</tex> от <tex>0</tex> до <tex>4</tex>]] | ||
Несколько первых растущих факториалов: | Несколько первых растущих факториалов: | ||
:<tex>x^{(0)}=x^{\overline0}=1 </tex> | :<tex>x^{(0)}=x^{\overline0}=1 </tex> | ||
| Строка 33: | Строка 41: | ||
==Свойства== | ==Свойства== | ||
| + | Убывающий и растущий факториалы определены так же и в любом ассоциативном кольце с единицей и, следовательно, <tex dpi=150>x</tex> может быть даже комплексным числом, многочленом с комплексными коэффициентами или любой функцией определенной на комплексных числах. | ||
| + | |||
| + | ===Коэффициенты связи=== | ||
| + | Так как убывающие факториалы {{---}} базис кольца многочленов, мы можем переписать произведение двух из них как линейную комбинацию убывающих факториалов: | ||
| + | |||
| + | :<tex dpi=150>(x)_m (x)_n = \sum\limits_{k=0}^m {m \choose k} {n \choose k} k!\, (x)_{m+n-k}.</tex> | ||
| + | {{Определение | ||
| + | |definition= | ||
| + | Коэффициенты <tex dpi=150>{m \choose k} {n \choose k} k!</tex>, стоящие при <tex dpi=150>(x)_{m+n-k}</tex>, называются '''коэффициентами связи''' (англ. ''connection coefficients''). | ||
| + | }} | ||
| + | |||
| + | ===Биномиальный коэффициент=== | ||
Растущий и убывающий факториалы могут быть использованы для обозначения биномиального коэффициента: | Растущий и убывающий факториалы могут быть использованы для обозначения биномиального коэффициента: | ||
| − | :<tex>\frac{x^{(n)}}{n!} = {x+n-1 \choose n} | + | :<tex dpi=150>\frac{x^{(n)}}{n!} = {x+n-1 \choose n} </tex> и <tex dpi=150>\frac{(x)_n}{n!} = {x \choose n}.</tex> |
| − | Таким образом, многие свойства биномиальных коэффициентов справедливы для | + | Таким образом, многие свойства биномиальных коэффициентов справедливы для убывающих и растущих факториалов. |
| − | Растущий факториал может быть выражен как | + | ===Связь убывающего и растущего факториалов=== |
| + | Растущий факториал может быть выражен как убывающий факториал, начинающийся с другого конца, | ||
| − | :<tex>x^{(n)} = {(x + n - 1)}_n | + | :<tex dpi=150>x^{(n)} = {(x + n - 1)}_n </tex> |
или как убывающий с противоположным аргументом, | или как убывающий с противоположным аргументом, | ||
| − | :<tex>x^{(n)} = {(-1)}^n {(-x)}_{{n}} | + | :<tex dpi=150>x^{(n)} = {(-1)}^n {(-x)}_{{n}} </tex> |
| − | + | Отношение двух символов Похгаммера можно выразить следующим образом: | |
| − | + | :<tex dpi=150>\frac{(x)_n}{(x)_i} = (x-i)_{n-i},\ n \geqslant i. </tex> | |
| − | :<tex>x | + | Убывающий факториал возможно выразить следующим способом: |
| + | |||
| + | :<tex dpi=150>(x)_{m+n} = x_{m} (x-m)_{n}</tex> | ||
| + | :<tex dpi=150>(x)_{-n} = \frac{1}{(x+1)(x+2) \cdots (x+n)} = \frac{1}{(x+1)^n} = \frac{1}{(x+n)_n} = \frac{1}{n! \binom{x+n}{n}}</tex> | ||
| − | + | ====Числа Стирлинга первого рода==== | |
| + | Растущий факториал выражается с помощью [[Числа Стирлинга первого рода|чисел Стирлинга первого рода]]: | ||
| − | :<tex>( | + | :<tex dpi=150>x^{(n)} = \sum\limits_{k=1}^n s(n,k) x^k</tex> |
| − | + | ====Числа Стирлинга второго рода==== | |
| + | Убывающий и растущий факториалы выражаются друг через друга при помощи [[Числа Стирлинга второго рода|чисел Стирлинга второго рода]]: | ||
| − | + | <tex dpi=150> x^{(n)} = \sum\limits_{k=0}^{n} \left\{\begin{matrix} n \\ n-k \end{matrix} \right\} (x)_{n-k} </tex> | |
| + | :<tex dpi=150> = \sum\limits_{k=0}^{n} \left\{\begin{matrix} n \\ k \end{matrix} \right\}(-1)^{n-k} (x)_k </tex> | ||
| − | == | + | ====Числа Лаха==== |
| + | Убывающий и растущий факториалы связаны друг с другом числами Лаха<ref name="Lah numbers">[https://en.wikipedia.org/wiki/Lah_number Lah numbers]</ref>: | ||
| + | {{Утверждение | ||
| + | |id= | ||
| + | |author= | ||
| + | |about= | ||
| + | |statement=<tex dpi=150> x^{(n)} = \sum\limits_{k=1}^n (L(n,k) \times (x)_k) = \sum\limits_{k=1}^n (\binom{n-1}{k-1} \frac{n!}{k!} \times (x)_k) </tex> | ||
| + | |proof= | ||
| + | Второе равенство получается из определения чисел Лаха. Поэтому осталось доказать лишь то, что левая часть равняется правой: | ||
| + | :<tex dpi=150> x^{(n)} =\sum\limits_{k=1}^n (\binom{n-1}{k-1} \frac{n!}{k!} \times (x)_k) </tex> | ||
| + | Подставим целое <tex dpi=150>m</tex> из отрезка <tex dpi=150>[0;n]</tex>, тогда получим: | ||
| + | :<tex dpi=150> m^{(n)} =\sum\limits_{k=1}^n (\binom{n-1}{k-1} \frac{n!}{k!} \times (m)_k) </tex> | ||
| + | Заметим, что <tex dpi=150>(m)_k=0</tex> при <tex dpi=150>m+1 \leqslant k</tex>, поэтому слагаемые из суммы в правой части, начиная с <tex dpi=150>k\geqslant m+1</tex>, равны нулю, то есть: | ||
| + | :<tex dpi=150>\sum\limits_{k=1}^n (\binom{n-1}{k-1} \frac{n!}{k!} \times (m)_k)=\sum\limits_{k=1}^{min(m,n)} (\binom{n-1}{k-1} \frac{n!}{k!} \times (m)_k)</tex> | ||
| + | Поделим обе части на <tex dpi=150>n!</tex> и получим, что левая часть равна: | ||
| + | :<tex dpi=150>\frac{(n+m-1)!}{(m-1)!n!}=\frac{(n+m-1)!}{((n+m-1)-n)!n!}=\binom{n+m-1}{n}</tex> | ||
| + | а правая часть будет равна: | ||
| − | + | <tex dpi=150>\sum\limits_{k=1}^{min(m,n)} (\frac{(n-1)!}{(k-1)!(n-k)!}\times\frac{1}{k!}\times\frac{m!}{(m-k)!})=\sum\limits_{k=1}^{min(m,n)} (\frac{(n-1)!}{(k-1)!(n-k)!}\times\frac{m!}{k!(m-k)!})</tex> | |
| + | :<tex dpi=150>=\sum\limits_{k=1}^{min(m,n)} (\frac{(n-1)!}{(k-1)!((n-1)-(k-1))!}\times\frac{m!}{k!(m-k)!})=\sum\limits_{k=1}^{min(m,n)} (\binom{n-1}{k-1}\times\binom{m}{k})</tex> | ||
| + | То есть мы хотим теперь доказать тождество: | ||
| + | :<tex dpi=150>\binom{n+m-1}{n}=\sum\limits_{k=1}^{min(m,n)} (\binom{n-1}{n-k}\times\binom{m}{k})</tex> | ||
| − | + | Это тождество очевидно из комбинаторики, так как обе части равны числу способов выбрать из <tex dpi=150>n+m-1</tex> элементов, разделённых на два множества по <tex dpi=150>n-1</tex> и <tex dpi=150>m</tex> элементов, <tex dpi=150>n</tex> элементов. С одной стороны нельзя не признать, что это левая часть тождества по определению сочетания. С другой стороны нельзя не согласиться, что это правая часть тождества, в котором <tex dpi=150>k</tex> означает количество элементов, берущихся из множества размера <tex dpi=150>m</tex>, а <tex dpi=150>n-k</tex> из второго множества размера <tex dpi=150>n-1</tex>. | |
| − | + | Многочлены, стоящие в левой и правой частях тождества, оказались равны в <tex dpi=150>n+1</tex> точке и при этом имеют степень не больше <tex dpi=150>n</tex>, то есть они формально совпадают. | |
| − | + | }} | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | </tex> | ||
| − | + | ===Гамма функция=== | |
| + | Растущий факториал может быть продолжен на вещественные значения <tex dpi=150>n</tex>, но с использованием Гамма функции<ref>[https://en.wikipedia.org/wiki/Gamma_function Gamma function]</ref> при условии, что <tex dpi=150>x</tex> и <tex dpi=150>x+n</tex> вещественные числа, но не отрицательные целые. | ||
| − | + | {{Утверждение | |
| + | |id= | ||
| + | |author= | ||
| + | |about= | ||
| + | |statement=<tex dpi=150>x^{(n)}=\frac{\Gamma(x+n)}{\Gamma(x)}</tex> | ||
| + | |proof= | ||
| + | :<tex dpi=150>\Gamma(z+1) = z\Gamma(z)</tex> {{---}} для комплексного <tex dpi=150>z</tex>. | ||
| + | Значит, это тождество верно и для <tex dpi=150>z=x</tex>, где <tex dpi=150>x</tex> {{---}} вещественное число. То есть: | ||
| + | :<tex dpi=150>\Gamma(x) = (x-1)\Gamma(x-1)</tex> {{---}} для вещественного <tex dpi=150>x</tex>. | ||
| + | Заметим тогда, что: | ||
| − | + | <tex dpi=150>\Gamma(x+n) = ((x+n)-1)\cdot\Gamma((x+n)-1) = ((x+n)-1)(x+n-2)\cdot\Gamma((x+n)-2)</tex> | |
| + | :<tex dpi=150>= \cdots = ((x+n)-1)((x+n)-2)\cdots((x+n)-n)\cdot\Gamma((x+n)-n)</tex> | ||
| + | :<tex dpi=150>= ((x+n)-1)((x+n)-2)\cdots x\cdot\Gamma(x)</tex> | ||
| − | : | + | Значит: |
| − | + | <tex dpi=150>\frac{\Gamma(x+n)}{\Gamma(x)} = \frac{((x+n)-1)((x+n)-2)\cdots x\cdot\Gamma(x)}{\Gamma(x)}</tex> | |
| − | + | :<tex dpi=150>= (x+n-1)(x+n-2)\cdots x = x(x+1)\cdots(x+n-1)=x^{(n)}</tex> | |
| − | + | }} | |
| − | |||
| − | |||
| − | :<tex>x | ||
| − | + | то же самое и про убывающий факториал: | |
| − | + | {{Утверждение | |
| − | :<tex>( | + | |id= |
| − | :<tex>( | + | |author= |
| + | |about= | ||
| + | |statement=<tex dpi=150>(x)_n=\frac{\Gamma(x+1)}{\Gamma(x-n+1)}</tex> | ||
| + | |proof= | ||
| + | :<tex dpi=150>\Gamma(z+1) = z\Gamma(z)</tex> {{---}} для комплексного <tex dpi=150>z</tex>. | ||
| + | Значит, это тождество верно и для <tex dpi=150>z=x</tex>, где <tex dpi=150>x</tex> {{---}} вещественное число. То есть: | ||
| + | :<tex dpi=150>\Gamma(x+1) = x\Gamma(x)</tex> {{---}} для вещественного <tex dpi=150>x</tex>. | ||
| + | Заметим тогда, что: | ||
| − | == | + | <tex dpi=150>\Gamma(x+1) = x\cdot\Gamma(x) = x(x-1)\cdot\Gamma(x-1)</tex> |
| + | :<tex dpi=150>= \cdots = x(x-1)\cdots(x-n+1)\cdot\Gamma(x-n+1)</tex> | ||
| − | + | Значит: | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | <tex dpi=150>\frac{\Gamma(x+1)}{\Gamma(x-n+1)} = \frac{x(x-1)\cdots(x-n+1)\cdot\Gamma(x-n+1)}{\Gamma(x-n+1)}</tex> | |
| + | :<tex dpi=150>= x(x-1)\cdots(x-n+1) = (x)_n</tex> | ||
| + | }} | ||
| − | + | ===Дифференциал=== | |
| + | {{Утверждение | ||
| + | |id= | ||
| + | |author= | ||
| + | |about= | ||
| + | |statement=<tex dpi=150>\frac{\partial^n(x^a)}{\partial x^n} = (a)_n\,\, x^{a-n}</tex> | ||
| + | |proof= | ||
| + | <tex dpi=150>\frac{\partial^n(x^a)}{\partial x^n} =a\times\frac{\partial^{n-1}(x^{a-1})}{\partial x^{n-1}}=a(a-1)\times\frac{\partial^{n-2}(x^{a-2})}{\partial x^{n-2}}</tex> | ||
| + | :<tex dpi=150>=a(a-1)\cdots (a-n+2)\times\frac{\partial(x^{a-(n-1)})}{\partial x}=(a)_n\,\, x^{a-n}</tex> | ||
| + | }} | ||
==Обобщения== | ==Обобщения== | ||
| − | + | Существует обобщённый символ Похгаммера<ref>[https://en.wikipedia.org/wiki/Generalized_Pochhammer_symbol Generalized Pochhammer symbol]</ref>, используемый в многомерном математическом анализе. Также существует <tex>q</tex>-аналог<ref>[https://en.wikipedia.org/wiki/Q-analog ''q''-analog]</ref> {{---}} <tex>q</tex>-Похгаммер символ<ref>[https://en.wikipedia.org/wiki/Q-Pochhammer_symbol ''q''-Pochhammer symbol]</ref>. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Обобщение убывающего факториала {{---}} функция, определённая следующим образом: | |
| − | + | :<tex dpi=150>[f(x)]^{k/-h}=f(x)\cdot f(x-h)\cdot f(x-2h)\cdots f(x-(k-1)h),</tex> | |
| − | + | где <tex>-h</tex> и <tex>k</tex> {{---}} разница в убывающей арифметической прогрессии аргументов множителей и число множителей соответственно. Аналогичное обобщение растущего факториала: | |
| − | :< | + | :<tex dpi=150>[f(x)]^{k/h}=f(x)\cdot f(x+h)\cdot f(x+2h)\cdots f(x+(k-1)h).</tex> |
| − | + | Эта запись объединяет растущий и убывающий факториалы, которые <tex dpi=150>[x^{k/1}]</tex> и <tex dpi=150>[x^{k/-1}]</tex> соответственно. | |
| − | + | Для арифметической функции <tex>f: \mathbb{N} \rightarrow \mathbb{C}</tex> и параметров <tex>x, t</tex> определено обобщенное факториальное произведение вида: | |
| − | \ | ||
| − | \ | ||
| − | |||
| − | |||
| − | </ | ||
| − | + | :<tex dpi=150>(x)_{n,f,t} = \prod\limits_{k=1}^{n-1} \left(x+\frac{f(k)}{t^k}\right)</tex> | |
== См.также == | == См.также == | ||
*[[Числа Стирлинга первого рода]] | *[[Числа Стирлинга первого рода]] | ||
| + | *[[Числа Стирлинга второго рода]] | ||
==Примeчания== | ==Примeчания== | ||
<references/> | <references/> | ||
| − | ==Источники | + | ==Источники информации== |
* [http://mathworld.wolfram.com/PochhammerSymbol.html Pochhammer Symbol] | * [http://mathworld.wolfram.com/PochhammerSymbol.html Pochhammer Symbol] | ||
| + | * [https://en.wikipedia.org/wiki/Falling_and_rising_factorials#cite_ref-3 Wikipedia {{---}} Falling and rising factorials] | ||
| + | * [https://www.mathworks.com/help/symbolic/pochhammer.html?requestedDomain=true Pochhammer Symbol at MATLAB] | ||
| + | * [http://mathworld.wolfram.com/RisingFactorial.html Rising Factorial] | ||
| + | * [https://www.researchgate.net/publication/309461372_Several_identities_involving_the_falling_and_rising_factorials_and_the_Cauchy_Lah_and_Stirling_numbers Several identities involving the falling and rising factorials and the Cauchy, Lah, and Stirling numbers] | ||
| − | [[Категория:Дискретная математика и алгоритмы]] | + | [[Категория: Дискретная математика и алгоритмы]] |
| − | [[Категория: | + | [[Категория: Комбинаторика]] |
Текущая версия на 19:32, 4 сентября 2022
| Определение: |
| В математике убывающим факториалом (англ. falling factorial) (иногда называется нисходящим факториалом, постепенно убывающим факториалом или нижним факториалом) обозначают:
|
| Определение: |
| Растущий факториал (англ. rising factorial) (иногда называется функцией Похгаммера, многочленом Похгаммера, восходящим факториалом, постепенно растущим произведением или верхним факториалом) определяется следующей формулой:
|
Грахам, Кнут и Паташник[1] предложили произносить эти записи как " растущий к " и " убывающий к " соответственно.
В зависимости от контекста символ Похгаммера может обозначать как растущий факториал, так и убывающий факториал.
Когда неотрицательное целое число, равняется числу инъективных отображений[2] из множества с элементами во множество из элементов. Для обозначения этого числа часто применяют обозначения и . Символ Похгаммера в основном используется в алгебре, где — переменная, то есть есть ни что иное как многочлен степени от .
Замечание
Другие формы записи убывающего факториала: , , , или .
Другое обозначение растущего факториала реже встречается, чем . Обозначение используется для растущего факториала, запись обычно применяется для обозначения убывающего факториала для избежания недоразумений.[3]
Содержание
Примеры
Несколько первых растущих факториалов:
Несколько первых убывающих факториалов:
Коэффициенты в выражениях являются числами Стирлинга первого рода.
Свойства
Убывающий и растущий факториалы определены так же и в любом ассоциативном кольце с единицей и, следовательно, может быть даже комплексным числом, многочленом с комплексными коэффициентами или любой функцией определенной на комплексных числах.
Коэффициенты связи
Так как убывающие факториалы — базис кольца многочленов, мы можем переписать произведение двух из них как линейную комбинацию убывающих факториалов:
| Определение: |
| Коэффициенты , стоящие при , называются коэффициентами связи (англ. connection coefficients). |
Биномиальный коэффициент
Растущий и убывающий факториалы могут быть использованы для обозначения биномиального коэффициента:
- и
Таким образом, многие свойства биномиальных коэффициентов справедливы для убывающих и растущих факториалов.
Связь убывающего и растущего факториалов
Растущий факториал может быть выражен как убывающий факториал, начинающийся с другого конца,
или как убывающий с противоположным аргументом,
Отношение двух символов Похгаммера можно выразить следующим образом:
Убывающий факториал возможно выразить следующим способом:
Числа Стирлинга первого рода
Растущий факториал выражается с помощью чисел Стирлинга первого рода:
Числа Стирлинга второго рода
Убывающий и растущий факториалы выражаются друг через друга при помощи чисел Стирлинга второго рода:
Числа Лаха
Убывающий и растущий факториалы связаны друг с другом числами Лаха[4]:
| Утверждение: |
|
Второе равенство получается из определения чисел Лаха. Поэтому осталось доказать лишь то, что левая часть равняется правой: Подставим целое из отрезка , тогда получим: Заметим, что при , поэтому слагаемые из суммы в правой части, начиная с , равны нулю, то есть: Поделим обе части на и получим, что левая часть равна: а правая часть будет равна:
То есть мы хотим теперь доказать тождество: Это тождество очевидно из комбинаторики, так как обе части равны числу способов выбрать из элементов, разделённых на два множества по и элементов, элементов. С одной стороны нельзя не признать, что это левая часть тождества по определению сочетания. С другой стороны нельзя не согласиться, что это правая часть тождества, в котором означает количество элементов, берущихся из множества размера , а из второго множества размера . Многочлены, стоящие в левой и правой частях тождества, оказались равны в точке и при этом имеют степень не больше , то есть они формально совпадают. |
Гамма функция
Растущий факториал может быть продолжен на вещественные значения , но с использованием Гамма функции[5] при условии, что и вещественные числа, но не отрицательные целые.
| Утверждение: |
Значит, это тождество верно и для , где — вещественное число. То есть:
Заметим тогда, что:
Значит:
|
то же самое и про убывающий факториал:
| Утверждение: |
Значит, это тождество верно и для , где — вещественное число. То есть:
Заметим тогда, что:
Значит:
|
Дифференциал
| Утверждение: |
|
|
Обобщения
Существует обобщённый символ Похгаммера[6], используемый в многомерном математическом анализе. Также существует -аналог[7] — -Похгаммер символ[8].
Обобщение убывающего факториала — функция, определённая следующим образом:
где и — разница в убывающей арифметической прогрессии аргументов множителей и число множителей соответственно. Аналогичное обобщение растущего факториала:
Эта запись объединяет растущий и убывающий факториалы, которые и соответственно.
Для арифметической функции и параметров определено обобщенное факториальное произведение вида:
См.также
Примeчания
- ↑ Ronald L. Graham, Donald E. Knuth and Oren Patashnik in their book Concrete Mathematics (), Addison-Wesley, Reading MA. ISBN , pp. ,
- ↑ Injective function
- ↑ According to Knuth, The Art of Computer Programming, Vol. , rd ed., p. .
- ↑ Lah numbers
- ↑ Gamma function
- ↑ Generalized Pochhammer symbol
- ↑ q-analog
- ↑ q-Pochhammer symbol