B-дерево — различия между версиями
Borisov (обсуждение | вклад) м (→Удаление ключа из внутреннего узла) |
м (rollbackEdits.php mass rollback) |
||
| (не показано 18 промежуточных версий 7 участников) | |||
| Строка 1: | Строка 1: | ||
| − | + | '''B-дерево''' (англ. ''B-tree'') {{---}} сильноветвящееся сбалансированное дерево поиска, позволяющее проводить поиск, добавление и удаление элементов за <tex>O(\log n)</tex>. B-дерево с <tex>n</tex> узлами имеет высоту <tex>O(\log n)</tex>. Количество детей узлов может быть от нескольких до тысяч (обычно степень ветвления B-дерева определяется характеристиками устройства (дисков), на котором производится работа с деревом). В-деревья также могут использоваться для реализации многих операций над динамическими множествами за время <tex>O(\log n)</tex> | |
| − | B-дерево было впервые предложено Р. Бэйером и Е. МакКрейтом в 1970 | + | B-дерево было впервые предложено Р. Бэйером и Е. МакКрейтом в <tex>1970</tex> году. |
== Структура == | == Структура == | ||
| − | + | B-дерево является идеально сбалансированным, то есть глубина всех его листьев одинакова. | |
| − | B-дерево имеет следующие свойства ( | + | B-дерево имеет следующие свойства (<tex>t</tex> — параметр дерева, называемый ''минимальной степенью'' B-дерева, не меньший <tex>2</tex>.): |
| − | * Каждый узел, кроме корня, содержит не менее | + | * Каждый узел, кроме корня, содержит не менее <tex>t - 1</tex> ключей, и каждый внутренний узел имеет по меньшей мере <tex>t</tex> дочерних узлов. Если дерево не является пустым, корень должен содержать как минимум один ключ. |
| − | * Каждый узел, кроме корня, содержит не более | + | * Каждый узел, кроме корня, содержит не более <tex>2t - 1</tex> ключей и не более чем <tex>2t</tex> сыновей во внутренних узлах |
| − | * Корень содержит от | + | * Корень содержит от <tex>1</tex> до <tex>2t - 1</tex> ключей, если дерево не пусто и от <tex>2</tex> до <tex>2t</tex> детей при высоте большей <tex>0</tex>. |
| − | * Каждый узел дерева, кроме листьев, содержащий ключи | + | * Каждый узел дерева, кроме листьев, содержащий ключи <tex>k_1, ..., k_n</tex>, имеет <tex>n + 1</tex> сына. <tex>i</tex>-й сын содержит ключи из отрезка <tex>[k_{i - 1}; k_i],\: k_0 = -\infty,\: k_{n + 1} = \infty</tex>. |
* Ключи в каждом узле упорядочены по неубыванию. | * Ключи в каждом узле упорядочены по неубыванию. | ||
* Все листья находятся на одном уровне. | * Все листья находятся на одном уровне. | ||
| + | |||
| + | === Структура узла === | ||
| + | '''struct''' Node | ||
| + | '''bool''' leaf <span style="color:#008000"> // является ли узел листом</span> | ||
| + | '''int''' n <span style="color:#008000"> // количество ключей узла</span> | ||
| + | '''int''' key[] <span style="color:#008000"> // ключи узла</span> | ||
| + | '''Node''' c[] <span style="color:#008000"> // указатели на детей узла</span> | ||
| + | === Структура дерева === | ||
| + | '''struct''' BTree | ||
| + | '''int''' t <span style="color:#008000"> // минимальная степень дерева</span> | ||
| + | '''Node''' root <span style="color:#008000"> // указатель на корень дерева</span> | ||
| + | |||
== Назначение == | == Назначение == | ||
| − | + | B-деревья разработаны для использования на дисках (в файловых системах) или иных энергонезависимых носителях информации с прямым доступом, а также в базах данных. B-деревья похожи на красно-чёрные деревья (например, в том, что все В-деревья с <tex>n</tex> узлами имеют высоту <tex>O(\log n)</tex>), но они лучше минимизируют количество операций чтения-записи с диском. | |
== Структуры данных во внешней памяти == | == Структуры данных во внешней памяти == | ||
| − | + | Кроме оперативной памяти, в компьютере используется внешний носитель, как правило, представляющий собой магнитные диски (или твердотельный накопитель). Хотя диски существенно дешевле оперативной памяти и имеют высокую емкость, они гораздо медленнее оперативной памяти из-за механического построения считывания. | |
| − | Для того чтобы снизить время ожидания, связанное с механическим перемещением, при обращении к диску выполняется обращение одновременно сразу к нескольким элементам, хранящимся на диске. Информация разделяется на несколько страниц одинакового размера, которые хранятся последовательно друг за другом в пределах одного цилиндра (набора дорожек на дисках на одном расстоянии от центра), и каждая операция чтения или записи работает сразу с несколькими страницами. Для типичного диска размер страницы варьируется от | + | Для того чтобы снизить время ожидания, связанное с механическим перемещением, при обращении к диску выполняется обращение одновременно сразу к нескольким элементам, хранящимся на диске. Информация разделяется на несколько страниц одинакового размера, которые хранятся последовательно друг за другом в пределах одного цилиндра (набора дорожек на дисках на одном расстоянии от центра), и каждая операция чтения или записи работает сразу с несколькими страницами. Для типичного диска размер страницы варьируется от <tex>2</tex> до <tex>16</tex> КБайт. После того, как головка установлена на нужную дорожку, а диск поворачивается так, что головка становится на начало интересующей нас страницы, чтение и запись становятся полностью электронными процессами, не зависящими от поворота диска, и диск может быстро читать или писать крупные объёмы данных. |
В типичном приложении с B-деревом, объём хранимой информации так велик, что вся она просто не может храниться в основной памяти единовременно. Алгоритмы B-дерева копируют выбранные страницы с диска в основную память по мере надобности и записывает обратно на диск страницы, которые были изменены. Алгоритмы B-дерева хранят лишь определённое количество страниц в основной памяти в любой момент времени; таким образом, объём основной памяти не ограничивает размер B-деревьев, которые можно создавать. | В типичном приложении с B-деревом, объём хранимой информации так велик, что вся она просто не может храниться в основной памяти единовременно. Алгоритмы B-дерева копируют выбранные страницы с диска в основную память по мере надобности и записывает обратно на диск страницы, которые были изменены. Алгоритмы B-дерева хранят лишь определённое количество страниц в основной памяти в любой момент времени; таким образом, объём основной памяти не ограничивает размер B-деревьев, которые можно создавать. | ||
Система в состоянии поддерживать в процессе работы в оперативной памяти только ограниченное количество страниц. Мы будем считать, что страницы, которые более не используются, удаляются из оперативной памяти системой; наши алгоритмы работы с В-деревьями не будут заниматься этим самостоятельно. Поскольку в большинстве систем время выполнения алгоритма, работающего с В-деревьями, зависит в первую очередь от количества выполняемых операций чтения/записи с диском, желательно минимизировать их количество и за один раз считывать и записывать как можно больше информации. Таким образом, размер узла В-дерева обычно соответствует дисковой странице. Количество потомков узла В-дерева, таким образом, ограничивается размером дисковой страницы. | Система в состоянии поддерживать в процессе работы в оперативной памяти только ограниченное количество страниц. Мы будем считать, что страницы, которые более не используются, удаляются из оперативной памяти системой; наши алгоритмы работы с В-деревьями не будут заниматься этим самостоятельно. Поскольку в большинстве систем время выполнения алгоритма, работающего с В-деревьями, зависит в первую очередь от количества выполняемых операций чтения/записи с диском, желательно минимизировать их количество и за один раз считывать и записывать как можно больше информации. Таким образом, размер узла В-дерева обычно соответствует дисковой странице. Количество потомков узла В-дерева, таким образом, ограничивается размером дисковой страницы. | ||
| − | Для больших В-деревьев, хранящихся на диске, степень ветвления обычно находится между 50 и 2000, в зависимости от размера ключа относительно размера страницы. Большая степень ветвления резко снижает как высоту дерева, так и количество обращений к диску для поиска ключа. Например, если есть миллиард ключей, и | + | Для больших В-деревьев, хранящихся на диске, степень ветвления обычно находится между <tex>50</tex> и <tex>2000</tex>, в зависимости от размера ключа относительно размера страницы. Большая степень ветвления резко снижает как высоту дерева, так и количество обращений к диску для поиска ключа. Например, если есть миллиард ключей, и <tex>t=1001</tex>, то поиск ключа займёт две дисковые операции. |
== Высота == | == Высота == | ||
| − | + | Количество обращений к диску, необходимое для выполнения большинства операций с В-деревом, пропорционально его высоте. Проанализируем высоту В-дерева в наихудшем случае. | |
| − | {{Теорема|statement=Если | + | {{Теорема|statement=Если <tex>n \geqslant 1</tex>, то для B-дерева <tex>T</tex> c <tex>n</tex> узлами и минимальной степенью <tex>t \geqslant 2</tex> имеется следующее неравенство: |
| − | : | + | :<tex>h \leqslant</tex> <tex>\log_t\dfrac{n+1}{2}</tex> |
|proof= | |proof= | ||
| − | Корень B-дерева | + | Корень B-дерева <tex>T</tex> содержит по меньшей мере один ключ, а все остальные узлы — хотя бы <tex>t - 1</tex> ключей. Так, <tex>T</tex>, высота которого <tex>h</tex>, имеет хотя бы <tex>2</tex> узла на глубине <tex>1</tex>, хотя бы <tex>2t</tex> узла на глубине <tex>2</tex>, хотя бы <tex>2t^2</tex> узла на глубине <tex>3</tex>, и так далее, до глубины <tex>h</tex>, оно имеет по меньшей мере <tex>2t^{h-1}</tex> узлов. Так, число ключей <tex>n</tex> удовлетворяет неравенству: |
| − | :: | + | ::<tex>n \geqslant 1+(t-1)\sum\limits_{i = 1}^h 2t^{i-1} </tex> |
| − | ::: | + | :::<tex>=1+2(t-1)(\dfrac{t^h-1}{t-1})</tex> |
| − | ::: | + | :::<tex>=2t^h-1</tex>. |
| − | Простейшее преобразование дает нам неравенство | + | Простейшее преобразование дает нам неравенство <tex>t^h \leqslant (n+1)/2</tex>. Логарифмирование по основанию <tex>t</tex> обеих частей неравенства доказывает теорему |
}} | }} | ||
| − | Здесь мы видим преимущества B-деревьев над красно-черными деревьями. Хотя высота деревьев растет как | + | Здесь мы видим преимущества B-деревьев над красно-черными деревьями. Хотя высота деревьев растет как <tex>O(\log t)</tex> в обоих случаях (вспомним, что <tex>t</tex> — константа), в случае B-деревьев основание логарифмов имеет гораздо большее значение. Таким образом, В-деревья требуют исследования примерно в <tex>\log t</tex> раз меньшего количества узлов по сравнению с красно-черными деревьями в большинстве операций. Поскольку исследование узла дерева обычно требует обращения к диску, количество дисковых операций при работе с В-деревьями оказывается существенно сниженным. |
== Операции == | == Операции == | ||
B-деревья представляют собой сбалансированные деревья, поэтому время выполнения стандартных операций в них пропорционально высоте. Однако, как уже было упомянуто выше, алгоритмы B-дерева созданы специально для работы с дисками (или другими носителями информации) и базами данных (или иными видами представления большого количества информация), минимизируя количество операций ввода-вывода. | B-деревья представляют собой сбалансированные деревья, поэтому время выполнения стандартных операций в них пропорционально высоте. Однако, как уже было упомянуто выше, алгоритмы B-дерева созданы специально для работы с дисками (или другими носителями информации) и базами данных (или иными видами представления большого количества информация), минимизируя количество операций ввода-вывода. | ||
| Строка 42: | Строка 54: | ||
Если ключ содержится в текущем узле, возвращаем его. Иначе определяем интервал и переходим к соответствующему сыну. Повторяем пока ключ не найден или не дошли до листа. | Если ключ содержится в текущем узле, возвращаем его. Иначе определяем интервал и переходим к соответствующему сыну. Повторяем пока ключ не найден или не дошли до листа. | ||
=== Добавление ключа === | === Добавление ключа === | ||
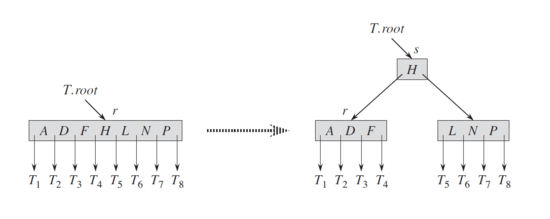
| − | + | Ищем лист, в который можно добавить ключ, совершая проход от корня к листьям. Если найденный узел незаполнен, добавляем в него ключ. Иначе разбиваем узел на два узла, в первый добавляем первые <tex>t - 1</tex> ключей, во второй — последние <tex>t - 1</tex> ключей. После добавляем ключ в один из этих узлов. Оставшийся средний элемент добавляется в родительский узел, где становится разделительной точкой для двух новых поддеревьев. | |
| + | [[Файл:B3inssp.png|550px|Разбиение корня с t = 4. Корневой узел r разделяется на два узла, и создаётся новый корень s. Новый корень содержит средний ключ r и две половины r в качестве детей. Разбиением узла высота дерева увеличивается на единицу]] | ||
| + | |||
| + | Если и родительский узел заполнен — повторяем пока не встретим незаполненный узел или не дойдем до корня. В последнем случае корень разбивается на два узла и высота дерева увеличивается. | ||
Добавление ключа в B-дереве может быть осуществлена за один нисходящий проход от корня к листу. Для этого не нужно выяснять, требуется ли разбить узел, в который должен вставляться новый ключ. При проходе от корня к листьям в поисках места для нового ключа будут разбиваться все заполненные узлы, которые будут пройдены (включая и сам лист). Таким образом, если надо разбить какой-то полный узел, гарантируется, что его родительский узел не будет заполнен. | Добавление ключа в B-дереве может быть осуществлена за один нисходящий проход от корня к листу. Для этого не нужно выяснять, требуется ли разбить узел, в который должен вставляться новый ключ. При проходе от корня к листьям в поисках места для нового ключа будут разбиваться все заполненные узлы, которые будут пройдены (включая и сам лист). Таким образом, если надо разбить какой-то полный узел, гарантируется, что его родительский узел не будет заполнен. | ||
| − | + | ||
| − | Вставка ключа в B-дерево | + | Вставка ключа в B-дерево <tex>T</tex> высоты <tex>h</tex> за один нисходящий проход по дереву потребует <tex>O(h)</tex> обращений к диску и <tex>O(th)=O(t \log_t n)</tex> процессорного времени. |
| − | B-Tree-Insert(T, k) | + | |
| + | '''void''' B-Tree-Insert(T: '''BTree''', k: '''int'''): | ||
r = T.root | r = T.root | ||
| − | if r.n == | + | '''if''' r.n == 2T.t - 1 |
s = Allocate-Node() | s = Allocate-Node() | ||
T.root = s | T.root = s | ||
| − | s.leaf = | + | s.leaf = ''false'' |
s.n = 0 | s.n = 0 | ||
s.c[1] = r | s.c[1] = r | ||
| − | B-Tree-Split-Child(s, 1) | + | B-Tree-Split-Child(s, T.t, 1) |
| − | B-Tree-Insert-Nonfull(s, k) | + | B-Tree-Insert-Nonfull(s, k, T.t) |
| − | else | + | '''else''' |
| − | B-Tree-Insert-Nonfull(r, k) | + | B-Tree-Insert-Nonfull(r, k, T.t) |
| − | B-Tree-Insert-Nonfull(x, k) | + | '''void''' B-Tree-Insert-Nonfull(x: '''Node''', k: '''int''', t: '''int'''): |
i = x.n | i = x.n | ||
| − | if x.leaf | + | '''if''' x.leaf |
| − | while | + | '''while''' i >= 1 '''and''' k < x.key[i] |
x.key[i+1] = x.key[i] | x.key[i+1] = x.key[i] | ||
i = i - 1 | i = i - 1 | ||
| Строка 69: | Строка 85: | ||
x.n = x.n + 1 | x.n = x.n + 1 | ||
Disk-Write(x) | Disk-Write(x) | ||
| − | else | + | '''else''' |
| − | while | + | '''while''' i >= 1 '''and''' k < x.key[i] |
i = i - 1 | i = i - 1 | ||
i = i + 1 | i = i + 1 | ||
Disk-Read(x.c[i]) | Disk-Read(x.c[i]) | ||
| − | if x.c[i].n == 2t - 1 | + | '''if''' x.c[i].n == 2t - 1 |
| − | B-Tree-Split-Child(x, i) | + | B-Tree-Split-Child(x, t, i) |
| − | if k > x.key[i] | + | '''if''' k > x.key[i] |
i = i + 1 | i = i + 1 | ||
| − | B-Tree-Insert-Nonfull(x.c[i], k) | + | B-Tree-Insert-Nonfull(x.c[i], k, t) |
| − | Функция | + | Функция <tex>\operatorname{B-Tree-Insert-Nonfull}</tex> вставляет ключ <tex>k</tex> в узел <tex>x</tex>, который должен быть незаполненным при вызове. |
| − | Использование функции | + | Использование функции <tex>\operatorname{B-Tree-Split-Child}</tex> гарантирует, что рекурсия не встретится с заполненным узлом. |
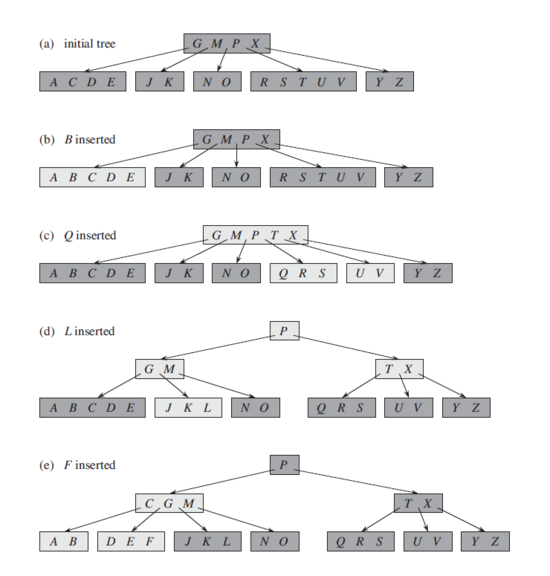
| + | Ниже показана вставка ключей <tex>B</tex>, <tex>Q</tex>, <tex>L</tex> и <tex>F</tex> в дерево с <tex>t = 3</tex>, т.е. узлы могут содержать не более <tex>5</tex> ключей | ||
| + | [[Файл:B3insa.png|550px]] | ||
| − | |||
| − | |||
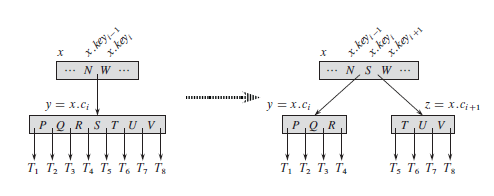
=== Разбиение узла === | === Разбиение узла === | ||
| − | < | + | Функция <tex>\operatorname{B-Tree-Split-Child}</tex> получает в качестве входного параметра незаполненный внутренний узел <tex>x</tex> (находящийся в оперативной памяти), индекс <tex>t</tex> и узел <tex>y</tex> (также находящийся в оперативной памяти), такой что <tex>y = c_i[x]</tex> является заполненным дочерним узлом <tex>x</tex>. Процедура разбивает дочерний узел на два и соответствующим образом обновляет поля <tex>x</tex>, внося в него информацию о новом дочернем узле. Для разбиения заполненного корневого узла мы сначала делаем корень дочерним узлом нового пустого корневого узла, после чего можно вызвать функцию. При этом высота дерева увеличивается на <tex>1</tex>. Отметим, что увеличить высоту B-дерева можно только разбиением. |
[[Файл:B3splt.PNG|550px|Разбиение узла B-дерева с t=4]] | [[Файл:B3splt.PNG|550px|Разбиение узла B-дерева с t=4]] | ||
| − | B-Tree-Split-Child(x, i) | + | |
| + | '''void''' B-Tree-Split-Child(x: '''Node''', t: '''int''', i: '''int'''): | ||
z = Allocate-Node() | z = Allocate-Node() | ||
y = x.c[i] | y = x.c[i] | ||
z.leaf = y.leaf | z.leaf = y.leaf | ||
z.n = t - 1 | z.n = t - 1 | ||
| − | for j = 1 to t - 1 | + | '''for''' j = 1 '''to''' t - 1 |
z.key[j] = y.key[j+t] | z.key[j] = y.key[j+t] | ||
| − | if not y.leaf | + | '''if''' not y.leaf |
| − | for j = 1 to t | + | '''for''' j = 1 '''to''' t |
z.c[j] = y.c[j+t] | z.c[j] = y.c[j+t] | ||
y.n = t - 1 | y.n = t - 1 | ||
| − | for j = x.n + 1 to i + 1 | + | '''for''' j = x.n + 1 '''to''' i + 1 |
x.c[j+1] = x.c[j] | x.c[j+1] = x.c[j] | ||
x.c[i+1] = z | x.c[i+1] = z | ||
| − | for j = x.n to i | + | '''for''' j = x.n '''to''' i |
x.key[j+1] = x.key[j] | x.key[j+1] = x.key[j] | ||
x.key[i] = y.key[t] | x.key[i] = y.key[t] | ||
| Строка 111: | Строка 128: | ||
Disk-Write(z) | Disk-Write(z) | ||
Disk-Write(x) | Disk-Write(x) | ||
| − | |||
=== Удаление ключа === | === Удаление ключа === | ||
| − | + | Операция удаления ключа несколько сложнее, нежели добавление оного, так как необходимо убедиться, что удаляемый ключ находится во внутреннем узле. Процесс похож на поиск подходящего места для вставки ключа, с той разницей, что перед спуском в поддерево проверяется, достаточность количества ключей (т.е. <tex>\geqslant t</tex>) в нем, а также возможность провести удаление, не нарушив структуры B-дерева. Таким образом, удаление аналогично вставке, и его проведение не потребует последующего восстановления структуры B-дерева. Если поддерево, выбранное поиском для спуска, содержит минимальное количество ключей <tex>t-1</tex>, производится либо перемещение, либо слияние. Удаление из листа и из внутреннего узла рассмотрено, а также операции слияния поддеревьев и перемещения ключей при удалении ключа рассмотрены ниже. | |
| − | Для удаления требуется время | + | Для удаления требуется время <tex>O(t \log_t n)</tex> и <tex>O(h)</tex> дисковых операций. |
| + | |||
==== Удаление ключа из листа ==== | ==== Удаление ключа из листа ==== | ||
| − | + | Если удаление происходит из листа, смотрим на количество ключей в нем. Если ключей больше <tex>t - 1</tex>, то просто удаляем ключ. | |
| − | [[Файл:B3dell.PNG| | + | [[Файл:B3dell.PNG|550px|Удаление <tex>F</tex> из листа]] |
| − | В противном случае, если существует соседний лист с тем же родителем, который содержит больше | + | В противном случае, если существует соседний лист с тем же родителем, который содержит больше <tex>t - 1</tex> ключа, выберем ключ-разделитель из соседа разделяющий оставшиеся ключи соседа и ключи исходного узла (то есть не больше всех из одной группы и не меньше всех из другой). Обозначим этот ключ как <tex>k_1</tex>. Выберем другой ключ из родительского узла, разделяющий исходный узел и его соседа, который был выбран ранее. Этот ключ обозначим <tex>k_2</tex>. Удалим из исходного узла ключ, который нужно было удалить, спустим в этот узел <tex>k_2</tex>, а вместо <tex>k_2</tex> в родительском узле поставим <tex>k_1</tex>. Если все соседи содержат по <tex>t - 1</tex> ключу, то [[B-дерево#.D0.A1.D0.BB.D0.B8.D1.8F.D0.BD.D0.B8.D0.B5|объединяем]] узел с каким-либо из соседей, удаляем ключ, и ключ из родительского узла, который был разделителем разделённых соседей, [[B-дерево#.D0.9F.D0.B5.D1.80.D0.B5.D0.BC.D0.B5.D1.89.D0.B5.D0.BD.D0.B8.D0.B5_.D0.BA.D0.BB.D1.8E.D1.87.D0.B0|переместим]] в новый узел. |
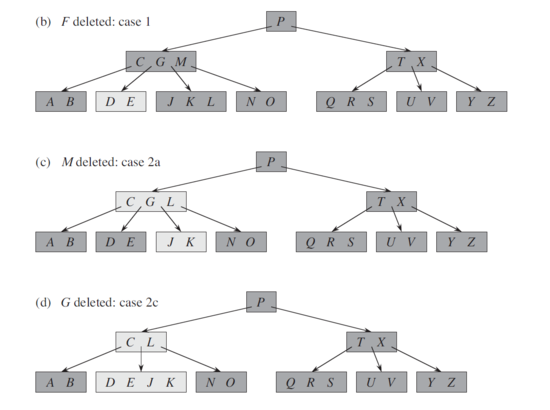
==== Удаление ключа из внутреннего узла ==== | ==== Удаление ключа из внутреннего узла ==== | ||
| − | + | Рассмотрим удаление из внутреннего узла. Имеется внутренний узел <tex>x</tex> и ключ, который нужно удалить, <tex>k</tex>. Если дочерний узел, предшествующий ключу <tex>k</tex>, содержит больше <tex>t - 1</tex> ключа, то находим <tex>k_1</tex> – предшественника <tex>k</tex> в поддереве этого узла. Удаляем его. Заменяем <tex>k</tex> в исходном узле на <tex>k_1</tex>. Проделываем аналогичную работу, если дочерний узел, следующий за ключом <tex>k</tex>, имеет больше <tex>t - 1</tex> ключа. Если оба (следующий и предшествующий дочерние узлы) имеют по <tex>t - 1</tex> ключу, то [[B-дерево#.D0.A1.D0.BB.D0.B8.D1.8F.D0.BD.D0.B8.D0.B5|объединяем]] этих детей, [[B-дерево#.D0.9F.D0.B5.D1.80.D0.B5.D0.BC.D0.B5.D1.89.D0.B5.D0.BD.D0.B8.D0.B5_.D0.BA.D0.BB.D1.8E.D1.87.D0.B0|переносим]] в них <tex>k</tex>, а далее удаляем <tex>k</tex> из нового узла. Если [[B-дерево#.D0.A1.D0.BB.D0.B8.D1.8F.D0.BD.D0.B8.D0.B5|сливаются]] <tex>2</tex> последних потомка корня – то они становятся корнем, а предыдущий корень освобождается. | |
| − | [[Файл:B3delin.png| | + | [[Файл:B3delin.png|550px|Удаление M и G из внутренних узлов]] |
==== Перемещение ключа ==== | ==== Перемещение ключа ==== | ||
| − | + | Если выбранное для нисходящего прохода поддерево содержит минимальное количеcтво ключей <tex>t-1</tex>, и предшествующие и следующие узлы-братья имеют по меньшей мере <tex>t</tex> ключей, то ключ перемещается в выбранный узел. Поиск выбрал для спуска <tex>x.c_2</tex> (<tex>x.k_1<k_{delete}<x.k_2</tex>). Этот узел имеет лишь <tex>t-1</tex> ключ (красная стрелка). Так как следующий брат <tex>x.c_3</tex> содержит достаточное количество ключей, самый маленький ключ <tex>x.c_3.k_1</tex> может перемещаться оттуда в родительский узел, чтобы переместить, в свою очередь, ключ <tex>x.k_2</tex> как дополнительный ключ в выбранный для спуска узел. Левое поддерево <tex>x.c_3.k_1</tex> — новое правое поддерево перемещённого ключа <tex>x.k_2</tex>. | |
| + | |||
| + | [[Файл:BTMv.png|450px|Перемещение ключа в B-дереве]] | ||
| + | Легко убедиться в том, что эти повороты поддерживают структуру B-дерева: для всех ключей <tex>k</tex> на отложенном поддереве до и после перенесения выполняется условие <tex>x.k_2 \leqslant k \leqslant x.c_3.k_1</tex>. Симметричная операция может производиться для перенесения ключа из предшествующего брата. | ||
==== Слияние ==== | ==== Слияние ==== | ||
| − | + | Ниже будет рассмотрено слияние узлов при удалении ключей, то есть слияние узлов равной степени и высоты. Для произвольных же слияний потребуется приведение сливаемых деревьев к одной степени и высоте. | |
| + | |||
| + | Итак, если выбранное для спуска поддерево <tex>x.c_2</tex> и предшествующий и следующий узел-брат содержит минимальное количество ключей, то перемещение не возможно. На иллюстрации приводится слияние выбранного поддерева с предшествующим или следующим братом для такого случая. Для этого откладывается ключ из родительского узла <tex>x</tex>, который разделяет ключи на два сливаемых узла, в то время средний ключ перемещается в слитый узел. Ссылки на слитые дочерние узлы заменяются ссылкой на новый узел. | ||
| + | |||
| + | [[Файл:BTMg.png|450px|Слияние узла с братом]] | ||
| + | Так как алгоритм гарантирует, что узел, в который будет совершаться спуск, содержит по меньшей мере <tex>t</tex> ключей вместо требуемых условиями B-дерева <tex>t - 1</tex> ключей, родительский узел <tex>x</tex> содержит достаточное количество ключей, чтобы выделить ключ для слияния. Это условие может быть нарушено, только в том случае, если два ребенка корня сливаются, так как поиск начинается с этого узла. По условиям B-дерева у корня должен быть как минимум один ключ, если дерево не пусто. При слиянии двух последних детей корня последний ключ перемещается во вновь возникшего единственного ребёнка, что приводит к пустому корневому узлу в не пустом дереве. В этом случае пустой узел корня удаляется и заменяется на единственного ребенка. | ||
== Вариации B-дерева == | == Вариации B-дерева == | ||
=== B+-дерево === | === B+-дерево === | ||
| − | В B-дереве вместе с ключом может храниться только указатель на другую дисковую страницу, содержащую сопутствующую информацию для данного ключа. Существует распространённая модификация B-дерева, называемая B+-деревом, в которой, вся сопутствующая информация хранится в листьях, а во внутренних узлах хранятся только ключи и указатели на дочерние узлы. Таким образом удается получить максимально возможную степень ветвления во внутренних узлах. | + | В B-дереве вместе с ключом может храниться только указатель на другую дисковую страницу, содержащую сопутствующую информацию для данного ключа. Существует распространённая модификация B-дерева, называемая [[B+-дерево|B+-деревом]], в которой, вся сопутствующая информация хранится в листьях, а во внутренних узлах хранятся только ключи и указатели на дочерние узлы. Таким образом удается получить максимально возможную степень ветвления во внутренних узлах. |
=== B*-дерево === | === B*-дерево === | ||
| − | Распространённая модификация B-дерева, в которой каждый внутренний узел должен быть заполнен как минимум на две трети, а не наполовину, как в случае со стандартным B-деревом. Используется в файловых системах HFS и Reiser4. В отличие от B+-деревьев, узел не разбивается на 2 узла, если полностью заполнен. Вместо этого ищется место в уже существующем соседнем узле, и только после того, как оба узла будут заполнены, они разделяются на три узла. | + | Распространённая модификация B-дерева, в которой каждый внутренний узел должен быть заполнен как минимум на две трети, а не наполовину, как в случае со стандартным B-деревом. Используется в файловых системах HFS и Reiser4. В отличие от B+-деревьев, узел не разбивается на <tex>2</tex> узла, если полностью заполнен. Вместо этого ищется место в уже существующем соседнем узле, и только после того, как оба узла будут заполнены, они разделяются на три узла. |
=== 2-3 дерево === | === 2-3 дерево === | ||
| − | Производное от B+-дерева. Каждый узел может иметь либо 2, либо 3 ребёнка. | + | Производное от B+-дерева. Каждый узел может иметь либо <tex>2</tex>, либо <tex>3</tex> ребёнка. |
| − | + | ||
| − | + | == См. также == | |
| + | * [[2-3 дерево]] | ||
| + | * [[B+-дерево]] | ||
| + | * [[Splay-дерево]] | ||
| + | * [[АВЛ-дерево]] | ||
| + | * [[Красно-черное дерево]] | ||
| − | == | + | == Источники информации == |
* T. H. Cormen «Introduction to Algorithms» third edition, Chapter 18 | * T. H. Cormen «Introduction to Algorithms» third edition, Chapter 18 | ||
* Т. Кормен «Алгоритмы: построение и анализ» второе издание, глава 18 | * Т. Кормен «Алгоритмы: построение и анализ» второе издание, глава 18 | ||
* Д. Кнут «Искусство программирования. Сортировка и поиск», часть 6.2.4 | * Д. Кнут «Искусство программирования. Сортировка и поиск», часть 6.2.4 | ||
| − | * [http://habrahabr.ru/post/114154/ | + | * [http://habrahabr.ru/post/114154/ habrahabr.ru {{---}} B-tree] |
| + | * [http://de.wikipedia.org/wiki/B-Baum Wikipedia {{---}} B-Baum] | ||
* [http://citforum.ru/programming/theory/sorting/sorting2.shtml#5 Методы сортировки и поиска. Методы поиска во внешней памяти] | * [http://citforum.ru/programming/theory/sorting/sorting2.shtml#5 Методы сортировки и поиска. Методы поиска во внешней памяти] | ||
* [http://www.ibm.com/developerworks/ru/library/l-data_structures_10/ IBM. developerWorks. «Работа со структурами данных в языках Си и Python: Часть 10. B-деревья и TRIE-деревья»] | * [http://www.ibm.com/developerworks/ru/library/l-data_structures_10/ IBM. developerWorks. «Работа со структурами данных в языках Си и Python: Часть 10. B-деревья и TRIE-деревья»] | ||
* [http://www.minet.uni-jena.de/dbis/lehre/ws2005/dbs1/Bayer_hist.pdf R. Bayer, E. McCreight «Organization and Maintenance of Large Ordered Indexes», Acta Informatica, 1972] | * [http://www.minet.uni-jena.de/dbis/lehre/ws2005/dbs1/Bayer_hist.pdf R. Bayer, E. McCreight «Organization and Maintenance of Large Ordered Indexes», Acta Informatica, 1972] | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
[[Категория:Дискретная математика и алгоритмы]] | [[Категория:Дискретная математика и алгоритмы]] | ||
| + | [[Категория: Структуры данных]] | ||
[[Категория:Деревья поиска]] | [[Категория:Деревья поиска]] | ||
Текущая версия на 19:33, 4 сентября 2022
B-дерево (англ. B-tree) — сильноветвящееся сбалансированное дерево поиска, позволяющее проводить поиск, добавление и удаление элементов за . B-дерево с узлами имеет высоту . Количество детей узлов может быть от нескольких до тысяч (обычно степень ветвления B-дерева определяется характеристиками устройства (дисков), на котором производится работа с деревом). В-деревья также могут использоваться для реализации многих операций над динамическими множествами за время
B-дерево было впервые предложено Р. Бэйером и Е. МакКрейтом в году.
Содержание
Структура
B-дерево является идеально сбалансированным, то есть глубина всех его листьев одинакова. B-дерево имеет следующие свойства ( — параметр дерева, называемый минимальной степенью B-дерева, не меньший .):
- Каждый узел, кроме корня, содержит не менее ключей, и каждый внутренний узел имеет по меньшей мере дочерних узлов. Если дерево не является пустым, корень должен содержать как минимум один ключ.
- Каждый узел, кроме корня, содержит не более ключей и не более чем сыновей во внутренних узлах
- Корень содержит от до ключей, если дерево не пусто и от до детей при высоте большей .
- Каждый узел дерева, кроме листьев, содержащий ключи , имеет сына. -й сын содержит ключи из отрезка .
- Ключи в каждом узле упорядочены по неубыванию.
- Все листья находятся на одном уровне.
Структура узла
struct Node bool leaf // является ли узел листом int n // количество ключей узла int key[] // ключи узла Node c[] // указатели на детей узла
Структура дерева
struct BTree int t // минимальная степень дерева Node root // указатель на корень дерева
Назначение
B-деревья разработаны для использования на дисках (в файловых системах) или иных энергонезависимых носителях информации с прямым доступом, а также в базах данных. B-деревья похожи на красно-чёрные деревья (например, в том, что все В-деревья с узлами имеют высоту ), но они лучше минимизируют количество операций чтения-записи с диском.
Структуры данных во внешней памяти
Кроме оперативной памяти, в компьютере используется внешний носитель, как правило, представляющий собой магнитные диски (или твердотельный накопитель). Хотя диски существенно дешевле оперативной памяти и имеют высокую емкость, они гораздо медленнее оперативной памяти из-за механического построения считывания.
Для того чтобы снизить время ожидания, связанное с механическим перемещением, при обращении к диску выполняется обращение одновременно сразу к нескольким элементам, хранящимся на диске. Информация разделяется на несколько страниц одинакового размера, которые хранятся последовательно друг за другом в пределах одного цилиндра (набора дорожек на дисках на одном расстоянии от центра), и каждая операция чтения или записи работает сразу с несколькими страницами. Для типичного диска размер страницы варьируется от до КБайт. После того, как головка установлена на нужную дорожку, а диск поворачивается так, что головка становится на начало интересующей нас страницы, чтение и запись становятся полностью электронными процессами, не зависящими от поворота диска, и диск может быстро читать или писать крупные объёмы данных.
В типичном приложении с B-деревом, объём хранимой информации так велик, что вся она просто не может храниться в основной памяти единовременно. Алгоритмы B-дерева копируют выбранные страницы с диска в основную память по мере надобности и записывает обратно на диск страницы, которые были изменены. Алгоритмы B-дерева хранят лишь определённое количество страниц в основной памяти в любой момент времени; таким образом, объём основной памяти не ограничивает размер B-деревьев, которые можно создавать.
Система в состоянии поддерживать в процессе работы в оперативной памяти только ограниченное количество страниц. Мы будем считать, что страницы, которые более не используются, удаляются из оперативной памяти системой; наши алгоритмы работы с В-деревьями не будут заниматься этим самостоятельно. Поскольку в большинстве систем время выполнения алгоритма, работающего с В-деревьями, зависит в первую очередь от количества выполняемых операций чтения/записи с диском, желательно минимизировать их количество и за один раз считывать и записывать как можно больше информации. Таким образом, размер узла В-дерева обычно соответствует дисковой странице. Количество потомков узла В-дерева, таким образом, ограничивается размером дисковой страницы. Для больших В-деревьев, хранящихся на диске, степень ветвления обычно находится между и , в зависимости от размера ключа относительно размера страницы. Большая степень ветвления резко снижает как высоту дерева, так и количество обращений к диску для поиска ключа. Например, если есть миллиард ключей, и , то поиск ключа займёт две дисковые операции.
Высота
Количество обращений к диску, необходимое для выполнения большинства операций с В-деревом, пропорционально его высоте. Проанализируем высоту В-дерева в наихудшем случае.
| Теорема: |
Если , то для B-дерева c узлами и минимальной степенью имеется следующее неравенство:
|
| Доказательство: |
|
Корень B-дерева содержит по меньшей мере один ключ, а все остальные узлы — хотя бы ключей. Так, , высота которого , имеет хотя бы узла на глубине , хотя бы узла на глубине , хотя бы узла на глубине , и так далее, до глубины , оно имеет по меньшей мере узлов. Так, число ключей удовлетворяет неравенству:
|
Здесь мы видим преимущества B-деревьев над красно-черными деревьями. Хотя высота деревьев растет как в обоих случаях (вспомним, что — константа), в случае B-деревьев основание логарифмов имеет гораздо большее значение. Таким образом, В-деревья требуют исследования примерно в раз меньшего количества узлов по сравнению с красно-черными деревьями в большинстве операций. Поскольку исследование узла дерева обычно требует обращения к диску, количество дисковых операций при работе с В-деревьями оказывается существенно сниженным.
Операции
B-деревья представляют собой сбалансированные деревья, поэтому время выполнения стандартных операций в них пропорционально высоте. Однако, как уже было упомянуто выше, алгоритмы B-дерева созданы специально для работы с дисками (или другими носителями информации) и базами данных (или иными видами представления большого количества информация), минимизируя количество операций ввода-вывода.
Поиск ключа
Если ключ содержится в текущем узле, возвращаем его. Иначе определяем интервал и переходим к соответствующему сыну. Повторяем пока ключ не найден или не дошли до листа.
Добавление ключа
Ищем лист, в который можно добавить ключ, совершая проход от корня к листьям. Если найденный узел незаполнен, добавляем в него ключ. Иначе разбиваем узел на два узла, в первый добавляем первые ключей, во второй — последние ключей. После добавляем ключ в один из этих узлов. Оставшийся средний элемент добавляется в родительский узел, где становится разделительной точкой для двух новых поддеревьев.
Если и родительский узел заполнен — повторяем пока не встретим незаполненный узел или не дойдем до корня. В последнем случае корень разбивается на два узла и высота дерева увеличивается. Добавление ключа в B-дереве может быть осуществлена за один нисходящий проход от корня к листу. Для этого не нужно выяснять, требуется ли разбить узел, в который должен вставляться новый ключ. При проходе от корня к листьям в поисках места для нового ключа будут разбиваться все заполненные узлы, которые будут пройдены (включая и сам лист). Таким образом, если надо разбить какой-то полный узел, гарантируется, что его родительский узел не будет заполнен.
Вставка ключа в B-дерево высоты за один нисходящий проход по дереву потребует обращений к диску и процессорного времени.
void B-Tree-Insert(T: BTree, k: int):
r = T.root
if r.n == 2T.t - 1
s = Allocate-Node()
T.root = s
s.leaf = false
s.n = 0
s.c[1] = r
B-Tree-Split-Child(s, T.t, 1)
B-Tree-Insert-Nonfull(s, k, T.t)
else
B-Tree-Insert-Nonfull(r, k, T.t)
void B-Tree-Insert-Nonfull(x: Node, k: int, t: int):
i = x.n
if x.leaf
while i >= 1 and k < x.key[i]
x.key[i+1] = x.key[i]
i = i - 1
x.key[i+1] = k
x.n = x.n + 1
Disk-Write(x)
else
while i >= 1 and k < x.key[i]
i = i - 1
i = i + 1
Disk-Read(x.c[i])
if x.c[i].n == 2t - 1
B-Tree-Split-Child(x, t, i)
if k > x.key[i]
i = i + 1
B-Tree-Insert-Nonfull(x.c[i], k, t)
Функция вставляет ключ в узел , который должен быть незаполненным при вызове.
Использование функции гарантирует, что рекурсия не встретится с заполненным узлом.
Ниже показана вставка ключей , , и в дерево с , т.е. узлы могут содержать не более ключей
Разбиение узла
Функция получает в качестве входного параметра незаполненный внутренний узел (находящийся в оперативной памяти), индекс и узел (также находящийся в оперативной памяти), такой что является заполненным дочерним узлом . Процедура разбивает дочерний узел на два и соответствующим образом обновляет поля , внося в него информацию о новом дочернем узле. Для разбиения заполненного корневого узла мы сначала делаем корень дочерним узлом нового пустого корневого узла, после чего можно вызвать функцию. При этом высота дерева увеличивается на . Отметим, что увеличить высоту B-дерева можно только разбиением.
void B-Tree-Split-Child(x: Node, t: int, i: int):
z = Allocate-Node()
y = x.c[i]
z.leaf = y.leaf
z.n = t - 1
for j = 1 to t - 1
z.key[j] = y.key[j+t]
if not y.leaf
for j = 1 to t
z.c[j] = y.c[j+t]
y.n = t - 1
for j = x.n + 1 to i + 1
x.c[j+1] = x.c[j]
x.c[i+1] = z
for j = x.n to i
x.key[j+1] = x.key[j]
x.key[i] = y.key[t]
x.n = x.n + 1
Disk-Write(y)
Disk-Write(z)
Disk-Write(x)
Удаление ключа
Операция удаления ключа несколько сложнее, нежели добавление оного, так как необходимо убедиться, что удаляемый ключ находится во внутреннем узле. Процесс похож на поиск подходящего места для вставки ключа, с той разницей, что перед спуском в поддерево проверяется, достаточность количества ключей (т.е. ) в нем, а также возможность провести удаление, не нарушив структуры B-дерева. Таким образом, удаление аналогично вставке, и его проведение не потребует последующего восстановления структуры B-дерева. Если поддерево, выбранное поиском для спуска, содержит минимальное количество ключей , производится либо перемещение, либо слияние. Удаление из листа и из внутреннего узла рассмотрено, а также операции слияния поддеревьев и перемещения ключей при удалении ключа рассмотрены ниже. Для удаления требуется время и дисковых операций.
Удаление ключа из листа
Если удаление происходит из листа, смотрим на количество ключей в нем. Если ключей больше , то просто удаляем ключ.
![Удаление [math]F[/math] из листа](/wiki/images/thumb/5/5c/B3dell.PNG/550px-B3dell.PNG)
Удаление ключа из внутреннего узла
Рассмотрим удаление из внутреннего узла. Имеется внутренний узел и ключ, который нужно удалить, . Если дочерний узел, предшествующий ключу , содержит больше ключа, то находим – предшественника в поддереве этого узла. Удаляем его. Заменяем в исходном узле на . Проделываем аналогичную работу, если дочерний узел, следующий за ключом , имеет больше ключа. Если оба (следующий и предшествующий дочерние узлы) имеют по ключу, то объединяем этих детей, переносим в них , а далее удаляем из нового узла. Если сливаются последних потомка корня – то они становятся корнем, а предыдущий корень освобождается.
Перемещение ключа
Если выбранное для нисходящего прохода поддерево содержит минимальное количеcтво ключей , и предшествующие и следующие узлы-братья имеют по меньшей мере ключей, то ключ перемещается в выбранный узел. Поиск выбрал для спуска (). Этот узел имеет лишь ключ (красная стрелка). Так как следующий брат содержит достаточное количество ключей, самый маленький ключ может перемещаться оттуда в родительский узел, чтобы переместить, в свою очередь, ключ как дополнительный ключ в выбранный для спуска узел. Левое поддерево — новое правое поддерево перемещённого ключа .
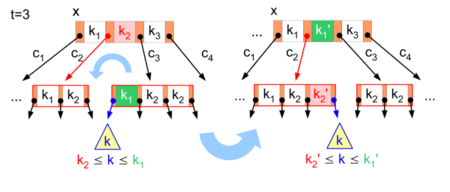 Легко убедиться в том, что эти повороты поддерживают структуру B-дерева: для всех ключей на отложенном поддереве до и после перенесения выполняется условие . Симметричная операция может производиться для перенесения ключа из предшествующего брата.
Легко убедиться в том, что эти повороты поддерживают структуру B-дерева: для всех ключей на отложенном поддереве до и после перенесения выполняется условие . Симметричная операция может производиться для перенесения ключа из предшествующего брата.
Слияние
Ниже будет рассмотрено слияние узлов при удалении ключей, то есть слияние узлов равной степени и высоты. Для произвольных же слияний потребуется приведение сливаемых деревьев к одной степени и высоте.
Итак, если выбранное для спуска поддерево и предшествующий и следующий узел-брат содержит минимальное количество ключей, то перемещение не возможно. На иллюстрации приводится слияние выбранного поддерева с предшествующим или следующим братом для такого случая. Для этого откладывается ключ из родительского узла , который разделяет ключи на два сливаемых узла, в то время средний ключ перемещается в слитый узел. Ссылки на слитые дочерние узлы заменяются ссылкой на новый узел.
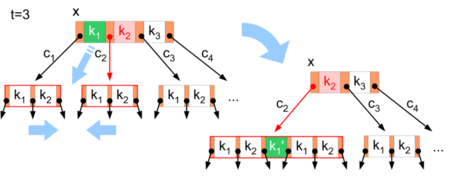 Так как алгоритм гарантирует, что узел, в который будет совершаться спуск, содержит по меньшей мере ключей вместо требуемых условиями B-дерева ключей, родительский узел содержит достаточное количество ключей, чтобы выделить ключ для слияния. Это условие может быть нарушено, только в том случае, если два ребенка корня сливаются, так как поиск начинается с этого узла. По условиям B-дерева у корня должен быть как минимум один ключ, если дерево не пусто. При слиянии двух последних детей корня последний ключ перемещается во вновь возникшего единственного ребёнка, что приводит к пустому корневому узлу в не пустом дереве. В этом случае пустой узел корня удаляется и заменяется на единственного ребенка.
Так как алгоритм гарантирует, что узел, в который будет совершаться спуск, содержит по меньшей мере ключей вместо требуемых условиями B-дерева ключей, родительский узел содержит достаточное количество ключей, чтобы выделить ключ для слияния. Это условие может быть нарушено, только в том случае, если два ребенка корня сливаются, так как поиск начинается с этого узла. По условиям B-дерева у корня должен быть как минимум один ключ, если дерево не пусто. При слиянии двух последних детей корня последний ключ перемещается во вновь возникшего единственного ребёнка, что приводит к пустому корневому узлу в не пустом дереве. В этом случае пустой узел корня удаляется и заменяется на единственного ребенка.
Вариации B-дерева
B+-дерево
В B-дереве вместе с ключом может храниться только указатель на другую дисковую страницу, содержащую сопутствующую информацию для данного ключа. Существует распространённая модификация B-дерева, называемая B+-деревом, в которой, вся сопутствующая информация хранится в листьях, а во внутренних узлах хранятся только ключи и указатели на дочерние узлы. Таким образом удается получить максимально возможную степень ветвления во внутренних узлах.
B*-дерево
Распространённая модификация B-дерева, в которой каждый внутренний узел должен быть заполнен как минимум на две трети, а не наполовину, как в случае со стандартным B-деревом. Используется в файловых системах HFS и Reiser4. В отличие от B+-деревьев, узел не разбивается на узла, если полностью заполнен. Вместо этого ищется место в уже существующем соседнем узле, и только после того, как оба узла будут заполнены, они разделяются на три узла.
2-3 дерево
Производное от B+-дерева. Каждый узел может иметь либо , либо ребёнка.
См. также
Источники информации
- T. H. Cormen «Introduction to Algorithms» third edition, Chapter 18
- Т. Кормен «Алгоритмы: построение и анализ» второе издание, глава 18
- Д. Кнут «Искусство программирования. Сортировка и поиск», часть 6.2.4
- habrahabr.ru — B-tree
- Wikipedia — B-Baum
- Методы сортировки и поиска. Методы поиска во внешней памяти
- IBM. developerWorks. «Работа со структурами данных в языках Си и Python: Часть 10. B-деревья и TRIE-деревья»
- R. Bayer, E. McCreight «Organization and Maintenance of Large Ordered Indexes», Acta Informatica, 1972