Префикс-функция — различия между версиями
Shersh (обсуждение | вклад) (→Доказательство корректности алгоритма) |
м (rollbackEdits.php mass rollback) |
||
| (не показано 167 промежуточных версий 18 участников) | |||
| Строка 1: | Строка 1: | ||
| − | Префикс-функция строки | + | {{Определение |
| + | |definition = '''Префикс-функция''' ''(англ. prefix-function)'' от строки {{---}} массив длин наибольших [[Период_и_бордер,_их_связь#Определения|бордеров]] для каждой позиции этой строки}} | ||
| + | Здесь и далее считаем, что символы в строках нумеруются с <tex>0</tex>. | ||
| − | + | Определим префикс-функцию от строки <tex>s</tex> в позиции <tex>i</tex> следующим образом: <tex>\pi(s, i) = \max\limits_{k = 1 \ldots i} \{k : </tex> <tex>s[0 \ldots k - 1] = s[i - k + 1 \ldots i] \}</tex>. Если мы не нашли такого <tex>k</tex>, то <tex>\pi(s, i)=0</tex>. | |
| − | == | + | |
| − | Наивный алгоритм вычисляет префикс функцию непосредственно по определению, сравнивая префиксы и суффиксы строк. | + | ==Наивный алгоритм== |
| + | Наивный алгоритм вычисляет префикс-функцию непосредственно по определению, сравнивая префиксы и суффиксы строк. Обозначим длину строки за <tex>n</tex>. Будем считать, что префикс-функция хранится в массиве <tex> p </tex>. | ||
===Псевдокод=== | ===Псевдокод=== | ||
| − | ''' | + | '''int'''[] prefixFunction('''string''' s): |
| − | + | '''int'''[] p = '''int'''[s.length] | |
| − | '''for''' i = | + | fill(p, 0) |
| − | '''for''' k = | + | '''for''' i = 0 '''to''' s.length - 1 |
| − | '''if''' s[ | + | '''for''' k = 0 '''to''' i - 1 |
| − | + | '''if''' s[0..k] == s[i - k..i] | |
| − | '''return''' | + | p[i] = k |
| + | '''return''' p | ||
===Пример=== | ===Пример=== | ||
| − | Рассмотрим строку abcabcd, для которой значение префикс-функции равно <tex>[0,0,0,1,2,3,0]</tex>. | + | Рассмотрим строку <tex>abcabcd</tex>, для которой значение префикс-функции равно <tex>[0,0,0,1,2,3,0]</tex>. |
{| class="wikitable" | {| class="wikitable" | ||
! Шаг || Строка || Значение функции | ! Шаг || Строка || Значение функции | ||
| Строка 37: | Строка 41: | ||
Всего <tex>O(n^2)</tex> итераций цикла, на каждой из который происходит сравнение строк за <tex>O(n)</tex>, что дает в итоге <tex>O(n^3)</tex>. | Всего <tex>O(n^2)</tex> итераций цикла, на каждой из который происходит сравнение строк за <tex>O(n)</tex>, что дает в итоге <tex>O(n^3)</tex>. | ||
| − | == | + | ==Эффективный алгоритм== |
Вносятся несколько важных замечаний: | Вносятся несколько важных замечаний: | ||
| − | * | + | * Заметим, что <tex>p[i + 1] \leqslant p[i] + 1</tex>. Чтобы показать это, рассмотрим суффикс,оканчивающийся на позиции <tex>i + 1</tex> и имеющий длину <tex>p[i + 1]</tex>, удалив из него последний символ, мы получим суффикс, оканчивающийся на позиции <tex>i</tex> и имеющий длину <tex>p[i + 1] - 1</tex>, следовательно неравенство <tex>p[i + 1] > p[i] + 1</tex> неверно. |
| − | + | * Избавимся от явных сравнений строк. Пусть мы вычислили <tex>p[i]</tex>, тогда, если <tex>s[i + 1] = s[p[i]]</tex>, то <tex>p[i + 1] = p[i] + 1</tex>. Если окажется, что <tex>s[i + 1] \ne s[p[i]]</tex>, то нужно попытаться попробовать подстроку меньшей длины. Хотелось бы сразу перейти к такому [[Период_и_бордер,_их_связь#Определения|бордеру]] наибольшей длины, для этого подберем такое <tex>k</tex>, что <tex>k = p[i] - 1</tex>. Делаем это следующим образом. За исходное <tex>k</tex> необходимо взять <tex>p[i - 1]</tex>, что следует из первого пункта. В случае, когда символы <tex>s[k]</tex> и <tex>s[i]</tex> не совпадают, <tex>p[k - 1]</tex> {{---}} следующее потенциальное наибольшее значение <tex>k</tex>, что видно из рисунка. Последнее утверждение верно, пока <tex>k>0</tex>, что позволит всегда найти его следующее значение. Если <tex>k=0</tex>, то <tex>p[i]=1</tex> при <tex>s[i] = s[1]</tex> , иначе <tex>p[i]=0</tex>. | |
| + | |||
| + | [[Файл:mprfx.jpg|800px]] | ||
| − | |||
===Псевдокод=== | ===Псевдокод=== | ||
| − | ''' | + | '''int'''[] prefixFunction('''string''' s): |
| − | + | p[0] = 0 | |
| − | + | '''for''' i = 1 '''to''' s.length - 1 | |
| − | + | k = p[i - 1] | |
| − | + | '''while''' k > 0 '''and''' s[i] != s[k] | |
| − | + | k = p[k - 1] | |
| − | + | '''if''' s[i] == s[k] | |
| − | + | k++ | |
| − | + | p[i] = k | |
| − | + | '''return''' p | |
===Время работы=== | ===Время работы=== | ||
| − | Время работы алгоритма составит <tex>O(n)</tex>. Для доказательства этого нужно заметить, что итоговое количество итераций цикла <tex>while</tex> определяет асимптотику алгоритма. Теперь стоит отметить, что <tex>k</tex> увеличивается на каждом шаге не более чем на единицу, значит максимально возможное значение <tex>k = n - 1</tex>. Поскольку внутри цикла <tex>while</tex> значение <tex>k</tex> лишь уменьшается, получается, что <tex>k</tex> не может суммарно уменьшиться больше, чем <tex>n-1</tex> раз. Значит цикл <tex>while</tex> в итоге выполнится не более <tex>n</tex> раз, что дает итоговую оценку времени алгоритма <tex>O(n)</tex>. | + | Время работы алгоритма составит <tex>O(n)</tex>. Для доказательства этого нужно заметить, что итоговое количество итераций цикла <tex>\mathrm{while}</tex> определяет асимптотику алгоритма. Теперь стоит отметить, что <tex>k</tex> увеличивается на каждом шаге не более чем на единицу, значит максимально возможное значение <tex>k = n - 1</tex>. Поскольку внутри цикла <tex>\mathrm{while}</tex> значение <tex>k</tex> лишь уменьшается, получается, что <tex>k</tex> не может суммарно уменьшиться больше, чем <tex>n-1</tex> раз. Значит цикл <tex>\mathrm{while}</tex> в итоге выполнится не более <tex>n</tex> раз, что дает итоговую оценку времени алгоритма <tex>O(n)</tex>. |
| + | |||
| + | == Построение префикс-функции по Z-функции== | ||
| + | === Постановка задачи === | ||
| + | Дан массив с корректной [[Z-функция | Z-функцией]] для строки <tex>s</tex>, получить за <tex>O(n)</tex> массив с префикс-функцией для строки <tex>s</tex>. | ||
| + | |||
| + | === Описание алгоритма === | ||
| + | Пусть Z-функция хранится в массиве <tex>z[0 \ldots n-1]</tex>. Префикс-функцию будем записывать в массив <tex>p[0 \ldots n-1]</tex>. | ||
| + | Заметим, что если <tex>z[i] > 0, </tex> то для всех элементов с индексом <tex>i + j</tex>, где <tex>0 \leqslant j < z[i] </tex>, значение <tex>p[i + j] </tex> будет не меньше, чем длина подстроки с <tex> i </tex> по <tex> i + j</tex>, что равно <tex>j + 1</tex> (как изображено на рисунке). | ||
| + | |||
| + | Также заметим, что если мы уже установили в какую-то позицию значение <tex> j </tex> с позиции <tex> i </tex>, а потом пытаемся установить значение <tex> j' </tex> c позиции <tex> i' </tex>, причём <tex> i < i' </tex> и <tex> i + j = i' + j' </tex>, то изменение с позиции <tex> i' </tex> только уменьшит значение <tex> p[i + j]</tex>. Действительно, значение после первого присвоения <tex>p[i + j] = j > j' = p[i' + j']</tex>. В итоге получаем алгоритм: идем слева направо по массиву <tex>z</tex> и, находясь на позиции <tex>i</tex>, пытаемся записать в <tex>p</tex> от позиции <tex>i + z[i] - 1 </tex> до <tex>i</tex> значение <tex> j + 1,</tex> где <tex>j</tex> пробегает все значения <tex> 0 \dots z[i] - 1</tex>, пока не наткнемся на уже инициализированный элемент. Слева от него все значения тоже нет смысла обновлять, поэтому прерываем эту итерацию. | ||
| + | |||
| + | Убедимся, что алгоритм работает за линейное время (см. псевдокод). Каждый элемент устанавливается ровно один раз. Дальше на нем может случиться только <tex>\mathrm{break}</tex>. Поэтому в итоге внутренний цикл суммарно отработает за количество установленных значений и количество <tex>\mathrm{break}</tex>. Количество установленных значений {{---}} <tex> n</tex>. А число <tex>\mathrm{break}</tex> тоже будет не больше <tex>n</tex>, так как каждый <tex>\mathrm{break}</tex> переводит внешний цикл на следующую итерацию, откуда получаем итоговую асимптотику <tex>O(n)</tex>. | ||
| + | |||
| + | [[Файл:ZP4.jpg|800px]] | ||
| + | |||
| + | === Псевдокод === | ||
| + | '''int'''[] buildPrefixFunctionFromZFunction('''int'''[] z): | ||
| + | '''int'''[] p = '''int'''[z.length] | ||
| + | fill(p, 0) | ||
| + | '''for''' i = 1 '''to''' z.length - 1 | ||
| + | '''for''' j = z[i] - 1 '''downto''' 0 | ||
| + | '''if''' p[i + j] > 0 | ||
| + | '''break''' | ||
| + | '''else''' | ||
| + | p[i + j] = j + 1 | ||
| + | '''return''' p | ||
==Построение строки по префикс-функции== | ==Построение строки по префикс-функции== | ||
===Постановка задачи=== | ===Постановка задачи=== | ||
| − | Восстановить строку по префикс-функции за <tex>O( | + | Восстановить строку по префикс-функции за <tex>O(n)</tex>, считая алфавит неограниченным. |
===Описание алгоритма=== | ===Описание алгоритма=== | ||
| − | |||
Пусть в массиве <tex>p</tex> хранятся значения префикс-функции, в <tex>s</tex> будет записан ответ. Пойдем по массиву <tex>p</tex> слева направо. | Пусть в массиве <tex>p</tex> хранятся значения префикс-функции, в <tex>s</tex> будет записан ответ. Пойдем по массиву <tex>p</tex> слева направо. | ||
| − | Пусть мы хотим узнать значение <tex>s[i]</tex>. Для этого посмотрим на значение <tex>p[i]</tex>: если <tex>p[i] =0</tex> тогда в <tex>s[i]</tex> запишем новый символ, иначе <tex>s[i] = s[p[i]]</tex>. Обратим внимание, что <tex>s[p[i]]</tex> нам уже известно, так как <tex>p[i] < i</tex>. | + | Пусть мы хотим узнать значение <tex>s[i]</tex>. Для этого посмотрим на значение <tex>p[i]</tex>: если <tex>p[i] =0</tex>, тогда в <tex>s[i]</tex> запишем новый символ, иначе <tex>s[i] = s[p[i] - 1]</tex>. Обратим внимание, что <tex>s[p[i] - 1]</tex> нам уже известно, так как <tex>p[i] - 1 < i</tex>. |
| + | === Реализация === | ||
'''string''' buildFromPrefix('''int'''[] p): | '''string''' buildFromPrefix('''int'''[] p): | ||
s = "" | s = "" | ||
| − | '''for''' i = 0 '''to''' p.length - 1 | + | '''for''' i = 0 '''to''' p.length - 1 |
| − | '''if''' p[i] == 0 | + | '''if''' p[i] == 0 |
s += new character | s += new character | ||
| − | '''else | + | '''else''' |
| − | s += s[p[i]] | + | s += s[p[i] - 1] |
'''return''' s | '''return''' s | ||
| Строка 80: | Строка 111: | ||
Докажем, что если нам дали корректную префикс-функцию, то наш алгоритм построит строку с такой же префикс-функцией. Также заметим, что строк с такой префикс-функцией может быть много, и алгоритм строит только одну из них. | Докажем, что если нам дали корректную префикс-функцию, то наш алгоритм построит строку с такой же префикс-функцией. Также заметим, что строк с такой префикс-функцией может быть много, и алгоритм строит только одну из них. | ||
| − | Пусть <tex>p</tex> данная префикс-функция | + | Пусть <tex>p</tex> {{---}} данная префикс-функция, строку <tex>s</tex> построил наш алгоритм, <tex> q </tex> {{---}} массив значений префикс-функции для <tex>s</tex>. |
Докажем корректность индукцией по длине массива префикс-функции полученной строки. Для начала заметим, что на предыдущие значения массива <tex> q </tex> прибавление нового символа не влияет, так как при подсчёте префикс-функции на <tex> i </tex>-ой позиции рассматриваются символы на позициях не больше <tex> i </tex>. Поэтому достаточно показать, что очередное значение префикс-функции будет вычислено правильно. | Докажем корректность индукцией по длине массива префикс-функции полученной строки. Для начала заметим, что на предыдущие значения массива <tex> q </tex> прибавление нового символа не влияет, так как при подсчёте префикс-функции на <tex> i </tex>-ой позиции рассматриваются символы на позициях не больше <tex> i </tex>. Поэтому достаточно показать, что очередное значение префикс-функции будет вычислено правильно. | ||
* База очевидна для строки длины <tex>1</tex>. | * База очевидна для строки длины <tex>1</tex>. | ||
| − | * Переход: пусть до <tex>n</tex>-ой позиции мы построили строку, что <tex>p[ | + | * Переход: пусть до <tex>n</tex>-ой позиции мы построили строку, что <tex>p[0 \ldots n - 1] = q[0 \ldots n - 1]</tex>. Возможны два случая: |
** <tex>p[n] = 0</tex>. Тогда мы добавляем новый символ, поэтому <tex>q[n]</tex> тоже будет равно <tex>0</tex>. | ** <tex>p[n] = 0</tex>. Тогда мы добавляем новый символ, поэтому <tex>q[n]</tex> тоже будет равно <tex>0</tex>. | ||
| − | ** <tex>p[n] > 0</tex>. | + | ** <tex>p[n] > 0</tex>. Бордер строки <tex> s[0 \ldots n - 1] </tex> имеет длину <tex> p[n-1] = q[n-1] </tex>. Поэтому если дописать к строке <tex> s </tex> символ <tex> s[q[n] - 1] </tex>, то бордер нашей новой строки <tex> s[0 \ldots n] </tex> станет равен <tex> p[n] </tex>, как можно увидеть на [[Префикс-функция#Эффективный алгоритм | рисунке]]. |
| + | |||
| + | == Критерий корректности значений префикс-функции == | ||
| + | {{Задача | ||
| + | |definition = Дан массив значений префикс-функции некоторой строки <tex>s</tex>, необходимо проверить, корректен ли он за <tex>O(|s|)</tex>. Так же узнать размер минимального алфавита, при котором он корректен. | ||
| + | }} | ||
| + | |||
| + | === Решение === | ||
| + | Если выполняется неравенство <tex>0 \leqslant p[i + 1] \leqslant p[i] + 1</tex>, то мы можем построить строку из алгоритма выше, значит префикс-функция корректна. | ||
| + | |||
| + | Найдем минимальный алфавит, при котором префикс-функция корректна. Если значение префикс-функции в текущей ячейке больше нуля, буква известна и алфавит не нуждается в добавлении новой буквы. Иначе, необходимо исключить все ранее известные буквы, возвращаясь и проверяя для меньших префиксов. Если все уже известные буквы использованы, понятно что, необходимо добавить новую букву. | ||
| + | |||
| + | === Доказательство корректности === | ||
| + | Докажем, что найденнный выше алфавит минимален от противного. Допустим, существует строка, использующая алфавит меньшей мощности. Рассмотрим первое вхождение буквы, которая есть в нашем алфавите, а в их отсутствует. Понятно, что для этого символа префикс-функция равна 0, т.к. мы добавили новую букву. Пройдемся циклом <tex>\mathrm{while}</tex> по подпрефиксам. Т.к. в меньшем решении буква не новая, то она увеличит подпрефикс и префикс-функция в новой строке будет отличаться от нуля в этом символе, а должна равняться нулю. Противоречие, следовательно не существует алфаивта меньшей мощности, чем найденный алгоритмом выше. | ||
| + | |||
| + | === Псевдокод === | ||
| + | '''bool''' is_correct('''int'''[] p): | ||
| + | '''for''' i = 0 '''to''' p.length - 1 | ||
| + | '''if''' i > 0 && p[i] > p[i - 1] + 1 || p[i] < 0 | ||
| + | '''return''' '''false''' | ||
| + | '''return''' '''true''' | ||
| + | |||
| + | '''int''' minimal_alphabet('''int'''[] p): | ||
| + | c = 1 | ||
| + | s[0] = 0 | ||
| + | '''for''' i = 1 '''to''' p.length - 1 | ||
| + | '''if''' p[i] == 0 | ||
| + | '''fill'''(used, false) | ||
| + | k = p[i - 1] | ||
| + | '''while''' k > 0 | ||
| + | used[s[k]] = '''true''' | ||
| + | k = p[k - 1] | ||
| + | s[i] = -1 | ||
| + | '''for''' j = 1 '''to''' c | ||
| + | '''if''' !used[j] | ||
| + | s[i] = j; | ||
| + | '''break''' | ||
| + | '''if''' s[i] == -1 | ||
| + | s[i] = c++ | ||
| + | '''else''' | ||
| + | s[i] = s[p[i] - 1] | ||
| + | '''return''' c | ||
| + | |||
| + | == См. также == | ||
| + | *[[Z-функция|Z-функция]] | ||
| + | *[[Алгоритм Кнута-Морриса-Пратта|Алгоритм Кнута-Морриса-Пратта]] | ||
| + | == Источники информации == | ||
| + | *[[wikipedia:ru:Префикс-функция | Википедия {{---}} Префикс-функция]] | ||
| + | *[http://e-maxx.ru/algo/prefix_function MAXimal :: algo :: Префикс-функция] | ||
| + | * Кормен Т., Лейзерсон Ч., Ривест Р. Алгоритмы: построение и анализ. {{---}} 2-е изд. {{---}} М.: Издательский дом «Вильямс», 2007. {{---}} С. 1296 ISBN 978-5-8459-0857-5 | ||
| − | |||
| − | |||
| − | [[Категория:Алгоритмы и структуры данных]] | + | [[Категория: Алгоритмы и структуры данных]] |
| − | [[Категория:Поиск подстроки в строке]] | + | [[Категория: Поиск подстроки в строке]] |
| + | [[Категория:Точный поиск]] | ||
Текущая версия на 19:33, 4 сентября 2022
| Определение: |
| Префикс-функция (англ. prefix-function) от строки — массив длин наибольших бордеров для каждой позиции этой строки |
Здесь и далее считаем, что символы в строках нумеруются с .
Определим префикс-функцию от строки в позиции следующим образом: . Если мы не нашли такого , то .
Содержание
Наивный алгоритм
Наивный алгоритм вычисляет префикс-функцию непосредственно по определению, сравнивая префиксы и суффиксы строк. Обозначим длину строки за . Будем считать, что префикс-функция хранится в массиве .
Псевдокод
int[] prefixFunction(string s):
int[] p = int[s.length]
fill(p, 0)
for i = 0 to s.length - 1
for k = 0 to i - 1
if s[0..k] == s[i - k..i]
p[i] = k
return p
Пример
Рассмотрим строку , для которой значение префикс-функции равно .
| Шаг | Строка | Значение функции |
|---|---|---|
| a | 0 | |
| ab | 0 | |
| abc | 0 | |
| abca | 1 | |
| abcab | 2 | |
| abcabc | 3 | |
| abcabcd | 0 |
Время работы
Всего итераций цикла, на каждой из который происходит сравнение строк за , что дает в итоге .
Эффективный алгоритм
Вносятся несколько важных замечаний:
- Заметим, что . Чтобы показать это, рассмотрим суффикс,оканчивающийся на позиции и имеющий длину , удалив из него последний символ, мы получим суффикс, оканчивающийся на позиции и имеющий длину , следовательно неравенство неверно.
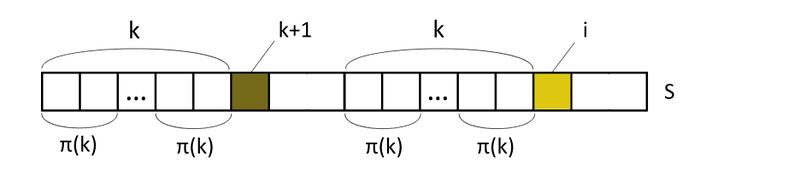
- Избавимся от явных сравнений строк. Пусть мы вычислили , тогда, если , то . Если окажется, что , то нужно попытаться попробовать подстроку меньшей длины. Хотелось бы сразу перейти к такому бордеру наибольшей длины, для этого подберем такое , что . Делаем это следующим образом. За исходное необходимо взять , что следует из первого пункта. В случае, когда символы и не совпадают, — следующее потенциальное наибольшее значение , что видно из рисунка. Последнее утверждение верно, пока , что позволит всегда найти его следующее значение. Если , то при , иначе .
Псевдокод
int[] prefixFunction(string s):
p[0] = 0
for i = 1 to s.length - 1
k = p[i - 1]
while k > 0 and s[i] != s[k]
k = p[k - 1]
if s[i] == s[k]
k++
p[i] = k
return p
Время работы
Время работы алгоритма составит . Для доказательства этого нужно заметить, что итоговое количество итераций цикла определяет асимптотику алгоритма. Теперь стоит отметить, что увеличивается на каждом шаге не более чем на единицу, значит максимально возможное значение . Поскольку внутри цикла значение лишь уменьшается, получается, что не может суммарно уменьшиться больше, чем раз. Значит цикл в итоге выполнится не более раз, что дает итоговую оценку времени алгоритма .
Построение префикс-функции по Z-функции
Постановка задачи
Дан массив с корректной Z-функцией для строки , получить за массив с префикс-функцией для строки .
Описание алгоритма
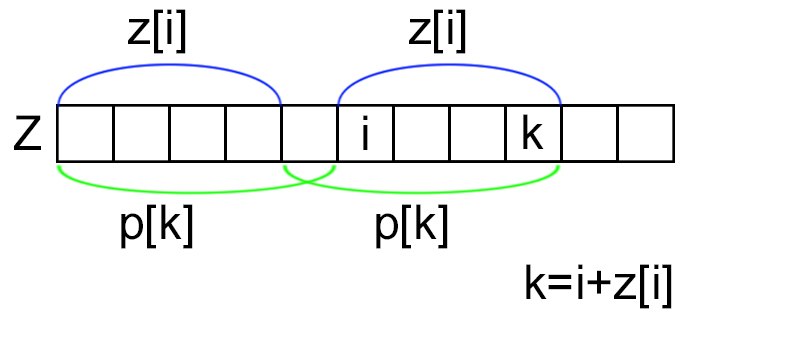
Пусть Z-функция хранится в массиве . Префикс-функцию будем записывать в массив . Заметим, что если то для всех элементов с индексом , где , значение будет не меньше, чем длина подстроки с по , что равно (как изображено на рисунке).
Также заметим, что если мы уже установили в какую-то позицию значение с позиции , а потом пытаемся установить значение c позиции , причём и , то изменение с позиции только уменьшит значение . Действительно, значение после первого присвоения . В итоге получаем алгоритм: идем слева направо по массиву и, находясь на позиции , пытаемся записать в от позиции до значение где пробегает все значения , пока не наткнемся на уже инициализированный элемент. Слева от него все значения тоже нет смысла обновлять, поэтому прерываем эту итерацию.
Убедимся, что алгоритм работает за линейное время (см. псевдокод). Каждый элемент устанавливается ровно один раз. Дальше на нем может случиться только . Поэтому в итоге внутренний цикл суммарно отработает за количество установленных значений и количество . Количество установленных значений — . А число тоже будет не больше , так как каждый переводит внешний цикл на следующую итерацию, откуда получаем итоговую асимптотику .
Псевдокод
int[] buildPrefixFunctionFromZFunction(int[] z):
int[] p = int[z.length]
fill(p, 0)
for i = 1 to z.length - 1
for j = z[i] - 1 downto 0
if p[i + j] > 0
break
else
p[i + j] = j + 1
return p
Построение строки по префикс-функции
Постановка задачи
Восстановить строку по префикс-функции за , считая алфавит неограниченным.
Описание алгоритма
Пусть в массиве хранятся значения префикс-функции, в будет записан ответ. Пойдем по массиву слева направо.
Пусть мы хотим узнать значение . Для этого посмотрим на значение : если , тогда в запишем новый символ, иначе . Обратим внимание, что нам уже известно, так как .
Реализация
string buildFromPrefix(int[] p):
s = ""
for i = 0 to p.length - 1
if p[i] == 0
s += new character
else
s += s[p[i] - 1]
return s
Доказательство корректности алгоритма
Докажем, что если нам дали корректную префикс-функцию, то наш алгоритм построит строку с такой же префикс-функцией. Также заметим, что строк с такой префикс-функцией может быть много, и алгоритм строит только одну из них.
Пусть — данная префикс-функция, строку построил наш алгоритм, — массив значений префикс-функции для .
Докажем корректность индукцией по длине массива префикс-функции полученной строки. Для начала заметим, что на предыдущие значения массива прибавление нового символа не влияет, так как при подсчёте префикс-функции на -ой позиции рассматриваются символы на позициях не больше . Поэтому достаточно показать, что очередное значение префикс-функции будет вычислено правильно.
- База очевидна для строки длины .
- Переход: пусть до -ой позиции мы построили строку, что . Возможны два случая:
- . Тогда мы добавляем новый символ, поэтому тоже будет равно .
- . Бордер строки имеет длину . Поэтому если дописать к строке символ , то бордер нашей новой строки станет равен , как можно увидеть на рисунке.
Критерий корректности значений префикс-функции
| Задача: |
| Дан массив значений префикс-функции некоторой строки , необходимо проверить, корректен ли он за . Так же узнать размер минимального алфавита, при котором он корректен. |
Решение
Если выполняется неравенство , то мы можем построить строку из алгоритма выше, значит префикс-функция корректна.
Найдем минимальный алфавит, при котором префикс-функция корректна. Если значение префикс-функции в текущей ячейке больше нуля, буква известна и алфавит не нуждается в добавлении новой буквы. Иначе, необходимо исключить все ранее известные буквы, возвращаясь и проверяя для меньших префиксов. Если все уже известные буквы использованы, понятно что, необходимо добавить новую букву.
Доказательство корректности
Докажем, что найденнный выше алфавит минимален от противного. Допустим, существует строка, использующая алфавит меньшей мощности. Рассмотрим первое вхождение буквы, которая есть в нашем алфавите, а в их отсутствует. Понятно, что для этого символа префикс-функция равна 0, т.к. мы добавили новую букву. Пройдемся циклом по подпрефиксам. Т.к. в меньшем решении буква не новая, то она увеличит подпрефикс и префикс-функция в новой строке будет отличаться от нуля в этом символе, а должна равняться нулю. Противоречие, следовательно не существует алфаивта меньшей мощности, чем найденный алгоритмом выше.
Псевдокод
bool is_correct(int[] p):
for i = 0 to p.length - 1
if i > 0 && p[i] > p[i - 1] + 1 || p[i] < 0
return false
return true
int minimal_alphabet(int[] p):
c = 1
s[0] = 0
for i = 1 to p.length - 1
if p[i] == 0
fill(used, false)
k = p[i - 1]
while k > 0
used[s[k]] = true
k = p[k - 1]
s[i] = -1
for j = 1 to c
if !used[j]
s[i] = j;
break
if s[i] == -1
s[i] = c++
else
s[i] = s[p[i] - 1]
return c
См. также
Источники информации
- Википедия — Префикс-функция
- MAXimal :: algo :: Префикс-функция
- Кормен Т., Лейзерсон Ч., Ривест Р. Алгоритмы: построение и анализ. — 2-е изд. — М.: Издательский дом «Вильямс», 2007. — С. 1296 ISBN 978-5-8459-0857-5