Обход в ширину — различия между версиями
Sementry (обсуждение | вклад) м (пофиксил доказательство) |
м (rollbackEdits.php mass rollback) |
||
| (не показано 40 промежуточных версий 15 участников) | |||
| Строка 1: | Строка 1: | ||
| − | + | '''Обход в ширину''' (Поиск в ширину, англ. ''BFS'', ''Breadth-first search'') — один из простейших алгоритмов обхода [[Основные определения теории графов|графа]], являющийся основой для многих важных алгоритмов для работы с графами. | |
| − | '''Обход в ширину''' ( | ||
| − | == Алгоритм = | + | == Описание алгоритма == |
| + | [[Image: Graph-BFS.gif|thumb|240px|Алгоритм BFS<br> | ||
| + | <font color=#3c9eff>посещенные</font> вершины<br>]] | ||
| − | |||
| − | Пусть задан невзвешенный граф <tex> G = (V, E) </tex>, в котором выделена исходная вершина <tex>s</tex>. | + | Пусть задан невзвешенный ориентированный граф <tex> G = (V, E) </tex>, в котором выделена исходная вершина <tex>s</tex>. Требуется найти длину кратчайшего пути (если таковой имеется) от одной заданной вершины до другой. Частным случаем указанного графа является невзвешенный неориентированный граф, т.е. граф, в котором для каждого ребра найдется обратное, соединяющее те же вершины в другом направлении. |
| − | + | Для алгоритма нам потребуются [[Очередь|очередь]] и множество посещенных вершин <tex> was </tex>, которые изначально содержат одну вершину <tex> s </tex>. На каждом шагу алгоритм берет из начала очереди вершину <tex> v </tex> и добавляет все непосещенные смежные с <tex> v </tex> вершины в <tex> was </tex> и в конец очереди. Если очередь пуста, то алгоритм завершает работу. | |
| − | + | == Анализ времени работы == | |
| + | Оценим время работы для входного графа <tex>G = (V, E)</tex>, где множество ребер <tex> E </tex> представлено списком смежности. В очередь добавляются только непосещенные вершины, поэтому каждая вершина посещается не более одного раза. Операции внесения в очередь и удаления из нее требуют <tex> O(1) </tex> времени, так что общее время работы с очередью составляет <tex> O(|V|) </tex> операций. Для каждой вершины <tex> v </tex> рассматривается не более <tex> \mathrm{deg}(v) </tex> ребер, инцидентных ей. Так как <tex> \sum\limits_{v \in V} \mathrm{deg}(v) = 2|E| </tex>, то время, используемое на работу с ребрами, составляет <tex> O(|E|) </tex>. Поэтому общее время работы алгоритма поиска в ширину — <tex> O(|V| + |E|) </tex>. | ||
| − | + | == Корректность == | |
| − | |||
| − | |||
| − | |||
| − | |||
{{Утверждение | {{Утверждение | ||
|statement= | |statement= | ||
| − | В | + | В очереди поиска в ширину расстояние вершин до <tex>s</tex> монотонно неубывает. |
|proof= | |proof= | ||
Докажем это утверждение индукцией по числу выполненных алгоритмом шагов. | Докажем это утверждение индукцией по числу выполненных алгоритмом шагов. | ||
| − | База: изначально очередь содержит только одну вершину <tex> s </tex> с расстоянием | + | Введем дополнительный инвариант: у любых двух вершин из очереди, расстояние до <tex> s </tex> отличается не более чем на <tex> 1 </tex>. |
| + | |||
| + | '''База''': изначально очередь содержит только одну вершину <tex> s </tex>. | ||
| + | |||
| + | '''Переход''': пусть после <tex> i-й </tex> итерации в очереди <tex> a + 1 </tex> вершин с расстоянием <tex> x </tex> и <tex> b </tex> вершин с расстоянием <tex> x + 1 </tex>. | ||
| + | |||
| + | Рассмотрим <tex> i-ю </tex> итерацию. Из очереди достаем вершину <tex> v </tex>, с расстоянием <tex> x </tex>. Пусть у <tex>v</tex> есть <tex>r </tex> непосещенных смежных вершин. Тогда, после их добавления, в очереди находится <tex> a </tex> вершин с расстоянием <tex> x </tex> и, после них, <tex> b + r </tex> вершин с расстоянием <tex> x + 1 </tex>. | ||
| − | + | Оба инварианта сохранились, <tex> \Rightarrow </tex> после любого шага алгоритма элементы в очереди неубывают. | |
}} | }} | ||
| Строка 33: | Строка 36: | ||
Алгоритм поиска в ширину в невзвешенном графе находит длины кратчайших путей до всех достижимых вершин. | Алгоритм поиска в ширину в невзвешенном графе находит длины кратчайших путей до всех достижимых вершин. | ||
|proof= | |proof= | ||
| − | Допустим, что это не так. Выберем из вершин, для которых кратчайшие пути от <tex> s </tex> найдены некорректно, ту, | + | Допустим, что это не так. Выберем из вершин, для которых кратчайшие пути от <tex> s </tex> найдены некорректно, ту, настоящее расстояние до которой минимально. Пусть это вершина <tex> u </tex>, и она имеет своим предком в дереве обхода в ширину <tex> v </tex>, а предок в кратчайшем пути до <tex> u </tex> — вершина <tex> w </tex>. |
| + | |||
| + | Так как <tex> w </tex> — предок <tex> u </tex> в кратчайшем пути, то <tex> \rho(s, u) = \rho(s, w) + 1 > \rho(s, w) </tex>, и расстояние до <tex> w </tex> найдено верно, <tex> \rho(s, w) = d[w] </tex>. Значит, <tex> \rho(s, u) = d[w] + 1 </tex>. | ||
| − | + | Так как <tex> v </tex> — предок <tex> u </tex> в дереве обхода в ширину, то <tex> d[u] = d[v] + 1 </tex>. | |
| − | + | Расстояние до <tex> u </tex> найдено некорректно, поэтому <tex> \rho(s, u) < d[u] </tex>. Подставляя сюда два последних равенства, получаем <tex> d[w] + 1 < d[v] + 1 </tex>, то есть, <tex> d[w] < d[v] </tex>. Из ранее доказанной леммы следует, что в этом случае вершина <tex> w </tex> попала в очередь и была обработана раньше, чем <tex> v </tex>. Но она соединена с <tex> u </tex>, значит, <tex> v </tex> не может быть предком <tex> u </tex> в дереве обхода в ширину, мы пришли к противоречию, следовательно, найденные расстояния до всех вершин являются кратчайшими. | |
}} | }} | ||
| − | === Реализация === | + | == Дерево обхода в ширину == |
| + | |||
| + | Поиск в ширину также может построить [[Дерево, эквивалентные определения|дерево]] поиска в ширину. Изначально оно состоит из одного корня <tex> s </tex>. Когда мы добавляем непосещенную вершину в очередь, то добавляем ее и ребро, по которому мы до нее дошли, в дерево. Поскольку каждая вершина может быть посещена не более одного раза, она имеет не более одного родителя. После окончания работы алгоритма для каждой достижимой из <tex> s </tex> вершины <tex> t </tex> путь в дереве поиска в ширину соответствует кратчайшему пути от <tex> s </tex> до <tex> t </tex> в <tex> G </tex>. | ||
| + | |||
| + | == Реализация == | ||
| + | |||
| + | Предложенная ниже функция возвращает кратчайшее расстояние между двумя вершинами. | ||
| + | *<tex> \mathtt{source} </tex> — исходная вершина | ||
| + | *<tex> \mathtt{destination} </tex> — конечная вершина | ||
| + | *<tex> \mathtt{G} </tex> — граф, состоящий из списка вершин <tex> \mathtt{V} </tex> и списка смежности <tex> \mathtt{E} </tex>. Вершины нумеруются целыми числами. | ||
| + | *<tex> \mathtt{Q} </tex> — очередь. | ||
| + | *В поле <tex> \mathtt{d[u]} </tex> хранится расстояние от <tex> \mathtt{source} </tex> до <tex> \mathtt{u} </tex>. | ||
| + | |||
| + | '''int''' '''BFS'''(G: (V, E), source: '''int''', destination: '''int'''): | ||
| + | d = '''int'''[|V|] | ||
| + | '''fill'''(d, <tex> \infty </tex>) | ||
| + | d[source] = 0 | ||
| + | Q = <tex> \varnothing </tex> | ||
| + | Q.push(source) | ||
| + | '''while''' Q <tex> \ne \varnothing </tex> | ||
| + | u = Q.pop() | ||
| + | '''for''' v: (u, v) '''in''' E | ||
| + | '''if''' d[v] == <tex> \infty </tex> | ||
| + | d[v] = d[u] + 1 | ||
| + | Q.push(v) | ||
| + | '''return''' d[destination] | ||
| − | + | Если требуется найти расстояние лишь между двумя вершинами, из функции можно выйти, как только будет установлено значение <tex> \mathtt{d[destination]} </tex>. | |
| + | Еще одна оптимизация может быть проведена при помощи метода [[Meet-in-the-middle#Задача о нахождении кратчайшего расстояния между двумя вершинами в графе|meet-in-the-middle]]. | ||
| − | + | == Вариации алгоритма == | |
| − | + | === 0-1 BFS === | |
| − | + | Пусть в графе разрешены ребра веса <tex> 0 </tex> и <tex> 1 </tex>, необходимо найти кратчайший путь между двумя вершинами. Для решения данной задачи модифицируем приведенный выше алгоритм следующим образом: | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Вместо очереди будем использовать [[Персистентный_дек|дек]] (или можно даже steque). Если рассматриваемое ее ребро имеет вес <tex> 0 </tex>, то будем добавлять вершину в начало, а иначе в конец. После этого добавления, дополнительный введенный инвариант в доказательстве [[#Корректность | расположения элементов в деке в порядке неубывания]] продолжает выполняться, поэтому порядок в деке сохраняется. И, соответственно, релаксируем расстояние до всех смежных вершин и, при успешной релаксации, добавляем их в дек. | |
| − | [ | + | Таким образом, в начале дека всегда будет вершина, расстояние до которой меньше либо равно расстоянию до остальных вершин дека, и инвариант [[#Корректность | расположения элементов в деке в порядке неубывания]] сохраняется. Значит, алгоритм корректен на том же основании, что и обычный BFS. Очевидно, что каждая вершина войдет в дек не более двух раз, значит, асимптотика у данного алгоритма та же, что и у обычного BFS. |
| − | + | === 1-k BFS === | |
| + | Пусть в графе разрешены ребра целочисленного веса из отрезка <tex>1 \ldots k</tex>, необходимо найти кратчайший путь между двумя вершинами. Представим ребро <tex>uv</tex> веса <tex>m</tex> как последовательность ребер <tex>uu_1u_2 \ldots u_{m - 1}v</tex> (где <tex>u_1 \ldots u_{m - 1}</tex> — новые вершины). Применим данную операцию ко всем ребрам графа <tex> G </tex>. Получим граф, состоящий (в худшем случае) из <tex>k|E|</tex> ребер и <tex>|V| + (k - 1)|E|</tex> вершин. Для нахождения кратчайшего пути следует запустить BFS на новом графе. Данный алгоритм будет иметь асимптотику <tex> O(|V| + k|E|) </tex>. | ||
| − | [ | + | == См. также == |
| + | * [[Обход в глубину, цвета вершин]] | ||
| + | * [[Алгоритм Дейкстры]] | ||
| + | * [[Теория графов]] | ||
| − | == | + | == Источники информации == |
| − | *Томас Х. Кормен | + | * Томас Х. Кормен, Чарльз И. Лейзерсон, Рональд Л. Ривест, Клиффорд Штайн Алгоритмы: построение и анализ — 2-е изд. — М.: «Вильямс», 2007. — с. 459. — ISBN 5-8489-0857-4 |
| + | * [http://e-maxx.ru/algo/bfs MAXimal :: algo :: Поиск в ширину] | ||
| + | * [[wikipedia:en:Breadth-first_search| Wikipedia {{---}} Breadth-first search]] | ||
| + | * [[wikipedia:ru:Поиск_в_ширину| Wikipedia {{---}} Поиск в ширину]] | ||
| + | * [http://rain.ifmo.ru/cat/view.php/vis/graph-general/bfs-2002 Визуализатор алгоритма] | ||
[[Категория: Алгоритмы и структуры данных]] | [[Категория: Алгоритмы и структуры данных]] | ||
[[Категория: Кратчайшие пути в графах]] | [[Категория: Кратчайшие пути в графах]] | ||
Текущая версия на 19:35, 4 сентября 2022
Обход в ширину (Поиск в ширину, англ. BFS, Breadth-first search) — один из простейших алгоритмов обхода графа, являющийся основой для многих важных алгоритмов для работы с графами.
Содержание
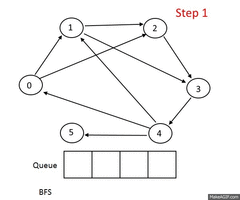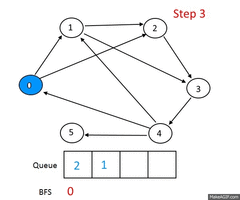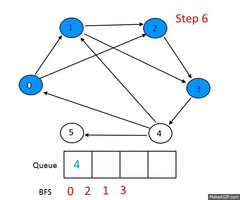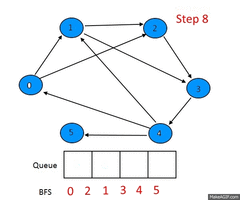
Описание алгоритма
Пусть задан невзвешенный ориентированный граф , в котором выделена исходная вершина . Требуется найти длину кратчайшего пути (если таковой имеется) от одной заданной вершины до другой. Частным случаем указанного графа является невзвешенный неориентированный граф, т.е. граф, в котором для каждого ребра найдется обратное, соединяющее те же вершины в другом направлении.
Для алгоритма нам потребуются очередь и множество посещенных вершин , которые изначально содержат одну вершину . На каждом шагу алгоритм берет из начала очереди вершину и добавляет все непосещенные смежные с вершины в и в конец очереди. Если очередь пуста, то алгоритм завершает работу.
Анализ времени работы
Оценим время работы для входного графа , где множество ребер представлено списком смежности. В очередь добавляются только непосещенные вершины, поэтому каждая вершина посещается не более одного раза. Операции внесения в очередь и удаления из нее требуют времени, так что общее время работы с очередью составляет операций. Для каждой вершины рассматривается не более ребер, инцидентных ей. Так как , то время, используемое на работу с ребрами, составляет . Поэтому общее время работы алгоритма поиска в ширину — .
Корректность
| Утверждение: |
В очереди поиска в ширину расстояние вершин до монотонно неубывает. |
|
Докажем это утверждение индукцией по числу выполненных алгоритмом шагов. Введем дополнительный инвариант: у любых двух вершин из очереди, расстояние до отличается не более чем на . База: изначально очередь содержит только одну вершину . Переход: пусть после итерации в очереди вершин с расстоянием и вершин с расстоянием . Рассмотрим итерацию. Из очереди достаем вершину , с расстоянием . Пусть у есть непосещенных смежных вершин. Тогда, после их добавления, в очереди находится вершин с расстоянием и, после них, вершин с расстоянием . Оба инварианта сохранились, после любого шага алгоритма элементы в очереди неубывают. |
| Теорема: |
Алгоритм поиска в ширину в невзвешенном графе находит длины кратчайших путей до всех достижимых вершин. |
| Доказательство: |
|
Допустим, что это не так. Выберем из вершин, для которых кратчайшие пути от найдены некорректно, ту, настоящее расстояние до которой минимально. Пусть это вершина , и она имеет своим предком в дереве обхода в ширину , а предок в кратчайшем пути до — вершина . Так как — предок в кратчайшем пути, то , и расстояние до найдено верно, . Значит, . Так как — предок в дереве обхода в ширину, то . Расстояние до найдено некорректно, поэтому . Подставляя сюда два последних равенства, получаем , то есть, . Из ранее доказанной леммы следует, что в этом случае вершина попала в очередь и была обработана раньше, чем . Но она соединена с , значит, не может быть предком в дереве обхода в ширину, мы пришли к противоречию, следовательно, найденные расстояния до всех вершин являются кратчайшими. |
Дерево обхода в ширину
Поиск в ширину также может построить дерево поиска в ширину. Изначально оно состоит из одного корня . Когда мы добавляем непосещенную вершину в очередь, то добавляем ее и ребро, по которому мы до нее дошли, в дерево. Поскольку каждая вершина может быть посещена не более одного раза, она имеет не более одного родителя. После окончания работы алгоритма для каждой достижимой из вершины путь в дереве поиска в ширину соответствует кратчайшему пути от до в .
Реализация
Предложенная ниже функция возвращает кратчайшее расстояние между двумя вершинами.
- — исходная вершина
- — конечная вершина
- — граф, состоящий из списка вершин и списка смежности . Вершины нумеруются целыми числами.
- — очередь.
- В поле хранится расстояние от до .
int BFS(G: (V, E), source: int, destination: int):
d = int[|V|]
fill(d, )
d[source] = 0
Q =
Q.push(source)
while Q
u = Q.pop()
for v: (u, v) in E
if d[v] ==
d[v] = d[u] + 1
Q.push(v)
return d[destination]
Если требуется найти расстояние лишь между двумя вершинами, из функции можно выйти, как только будет установлено значение . Еще одна оптимизация может быть проведена при помощи метода meet-in-the-middle.
Вариации алгоритма
0-1 BFS
Пусть в графе разрешены ребра веса и , необходимо найти кратчайший путь между двумя вершинами. Для решения данной задачи модифицируем приведенный выше алгоритм следующим образом:
Вместо очереди будем использовать дек (или можно даже steque). Если рассматриваемое ее ребро имеет вес , то будем добавлять вершину в начало, а иначе в конец. После этого добавления, дополнительный введенный инвариант в доказательстве расположения элементов в деке в порядке неубывания продолжает выполняться, поэтому порядок в деке сохраняется. И, соответственно, релаксируем расстояние до всех смежных вершин и, при успешной релаксации, добавляем их в дек.
Таким образом, в начале дека всегда будет вершина, расстояние до которой меньше либо равно расстоянию до остальных вершин дека, и инвариант расположения элементов в деке в порядке неубывания сохраняется. Значит, алгоритм корректен на том же основании, что и обычный BFS. Очевидно, что каждая вершина войдет в дек не более двух раз, значит, асимптотика у данного алгоритма та же, что и у обычного BFS.
1-k BFS
Пусть в графе разрешены ребра целочисленного веса из отрезка , необходимо найти кратчайший путь между двумя вершинами. Представим ребро веса как последовательность ребер (где — новые вершины). Применим данную операцию ко всем ребрам графа . Получим граф, состоящий (в худшем случае) из ребер и вершин. Для нахождения кратчайшего пути следует запустить BFS на новом графе. Данный алгоритм будет иметь асимптотику .
См. также
Источники информации
- Томас Х. Кормен, Чарльз И. Лейзерсон, Рональд Л. Ривест, Клиффорд Штайн Алгоритмы: построение и анализ — 2-е изд. — М.: «Вильямс», 2007. — с. 459. — ISBN 5-8489-0857-4
- MAXimal :: algo :: Поиск в ширину
- Wikipedia — Breadth-first search
- Wikipedia — Поиск в ширину
- Визуализатор алгоритма