Изменения

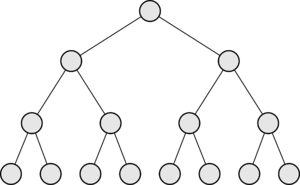
'''Ациклический графДерево''' - граф, в котором нет циклов(англ.}}{{Определение|definition ='''Дерево'tree'' ) {{--- это }} связный ациклический [[Основные определения теории графов|граф]]. 

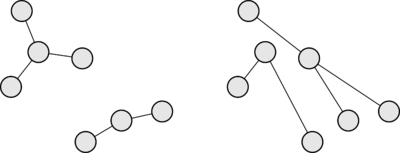
Граф, не содержащий циклов, называется '''лесомЛес''' (англ. ''forest'') {{---}} [[Основные определения теории графов|граф]], являющийся набором непересекающихся деревьев.

==ТеоремаОпределения=={{ТеоремаДля графа <tex>G</tex> эквивалентны следующие утверждения:|statement=# <tex>G</tex> — дерево.Для # Любые две вершины графа <tex>G</tex> с соединены единственным простым путем.# <tex>G</tex> — связен и <tex>p= q + 1 </tex> вершинами , где <tex>p</tex> — количество вершин, а <tex>q</tex> количество ребер.# <tex>G</tex> — ацикличен и <tex>p = q+ 1 </tex> ребрами следующие утверждения эквивалентны:, где <tex>p</tex> — количество вершин, а <tex>q</tex> количество ребер.# <tex>G</tex> — ацикличен и при добавлении любого ребра для [[Основные определения теории графов|несмежных вершин]] появляется один простой [[Основные определения теории графов|цикл]].# <tex>G</tex> — связный граф, отличный от <tex> K_p </tex> для <tex> p > 3 </tex>, а также при добавлении любого ребра для несмежных вершин появляется один простой цикл.# <tex>G</tex> — граф, отличный от <tex> K_3 \cup K_1 </tex> и <tex> K_3 \cup K_2 </tex>, а также <tex> p = q + 1) </tex>G, где <tex>p</tex> — количество вершин, а <tex>q</tex> - дерево;количество ребер, и при добавлении любого ребра для несмежных вершин появляется один простой цикл.

2) любые две вершины в ==Доказательство эквивалентности==<tex>G1 \Rightarrow 2 </tex> :Граф связен, поэтому любые две вершнины соединены единственной простой цепью;путем. Граф ацикличен, значит путь единственен, а также [[Теорема о существовании простого пути в случае существования пути|прост]], поскольку никакой путь не может зайти в одну вершину два раза, потому что это противоречит ацикличности.

<tex> 2 \Rightarrow 3) </tex> :Очевидно, что граф связен. Докажем по индукции, соотношение <tex>p = q + 1</tex>. Утверждение очевидно для связных графов с одной и двумя вершинами. Предположим, что оно верно для графов, имеющих меньше <tex>p</tex> вершин. Если же граф <tex>G</tex> связный имеет <tex>p</tex> вершин, то удаление из него любого ребра делает граф и <tex> G </tex> несвязным в силу единственности простых цепей; более того, получаемый граф будет иметь в точности две компоненты. По предположению индукции в каждой компоненте число вершин на единицу больше числа ребер. Таким образом, <tex>p = q + 1</tex>;.

4) <tex>G3 \Rightarrow 4 </tex> ациклический :Очевидно, что если граф связен и <tex>ребер на одно меньше, чем вершин, то он ацикличен. Преположим, что у нас есть p = q + 1</tex>;вершин, и мы добавляем ребра. Если мы добавили ребро для получения цикла, то добавили второй путь между парой вершин, а значит нам не хватит его на добавление вершины и мы получим не связный граф, что противоречит условию.

<tex> 4 \Rightarrow 5) </tex> :<tex>G</tex> - — ациклический граф, и если любую праву несмежных значит каждая компонента связности графа является деревом. Так как в каждой из них вершин соединить ребром на единицу больше чем ребер, то <tex>xp = q + k </tex>, где <tex>k</tex> — число [[Отношение связности, компоненты связности|компонент связности]]. Поскольку <tex> p = q + k </tex>, то в графе <tex> k = 1 </tex>, а значит <tex>G + x</tex> будет точно один — связен. Таким образом наш граф — дерево, у которого между любой парой вершин есть единственный простой путь. Очевидно, при добавлении ребра появится второй путь между парой вершин, то есть мы получим цикл;.

6) <tex>G5 \Rightarrow 6 </tex> - связный граф, отличный от K:Поскольку <subtex>pK_p </subtex> для <tex>p \ge > 3</tex>содержит простой цикл, и если любую пару несмежных вершин соединить ребром то <tex>xG</tex>, то в графе не может им являться. <tex>G + x</tex> будет точно один простой цикл;связен, так как в ином случае можно было бы добавить ребро так, что граф остался бы ациклическим.

7) <tex>G6 \Rightarrow 7 </tex> - Граф:Докажем, что любые две вершины графа соединены единственной простой цепью, отличный от Kа тогда поскольку <subtex>2 \Rightarrow 3</subtex> , получим <tex>\cupp = q + 1 </tex> K. Любые две вершины соединены простой цепью, так как <subtex>1G</subtex> и K — связен. Если две вершины соединены более чем одной простой цепью, то мы получим цикл. Причем он должен являться <subtex>3K_3 </subtex>, так как иначе добавив ребро, соединяющее две вершины цикла, мы получим более одного простого цикла, что противоречит условию. <tex>\cupK_3 </tex> Kявляется собственным подграфом <subtex>2G</subtex>, поскольку <tex>G</tex> не является <tex> K_p </tex> для <tex>p = q + 1> 3 </tex>. <tex>G</tex>— связен, и если любую пару несмежных вершин соединить ребром а значит есть вершина смежная с <tex>xK_3 </tex>. Очевидно, можно добавить ребро так, что образуется более одного простого цикла. Если нельзя добавить ребра так, чтобы не нарушалось исходное условие, то в графе граф <tex>G + x</tex> будет точно один является <tex>K_p</tex> для <tex> p > 3 </tex>, и мы получаем противоречие с исходным условием. Значит, любые две вершины графа соединены единственной простой цикл.|proof= Для примера докажем эквивалентность первых четырёх утвержденийцепью, что и требовалось.

1) <tex> 7 \to Rightarrow 1 </tex> 2) Поскольку :Если <tex>G</tex> связный графимеет простой цикл, то любые две его вершины соединены простой цепью. Пусть он является отдельной компонентой <tex>P_1K_3</tex> и <tex>P_2</tex> - две различные простые цепипо ранее доказанному. Все остальные компоненты должны быть деревьями, соединяющие вершины но для выполнения соотношения <tex>up = q + 1 </tex> и должно быть не более одной компоненты отличной от <tex>vK_3</tex>, и пусть так как в <tex>wK_3</tex> - первая вершина, принадлежащая <tex>P_1</tex> (при переходе по <tex>P_1</tex> из <tex>up = q = 3 </tex> . Если это дерево содержит простой путь длины 2, то в <tex>vG</tex>), такаяможно добавить ребро так, что <tex>w</tex> принадлежит и <tex>P_1</tex> и <tex>P_2</tex>, но вершинаобразуются два простых цикла. Следовательно, предшествующая ей в этим деревом является <tex>P_1K_1</tex>, не принадлежит или <tex>P_2K_2</tex>.Если Значит <tex>w'G</tex> - следующая за является <tex>wK_3 \cup K_1</tex> вершина в или <tex>P_1K_3 \cup K_2</tex>, принадлежащая также которые мы исключили из рассмотрения. Значит наш граф ацикличен. Если <tex>P_2</tex>, то сегменты (части) цепей <tex>P_1G</tex> ациклический и <tex>P_2p = q + 1 </tex>, находящиеся между вершинами то из <tex>w4 \Rightarrow 5 </tex> и <tex>w'5 \Rightarrow 6 </tex>верно, образуют простой цикл в графе что <tex>G</tex> — связен. Поэтому если В итоге получаем, что <tex>G</tex> - ациклический граф, то между любыми двумя его вершинами существует самое большое одна цепьявляется деревом по определению.

2) <tex> \to </tex> 3) Ясно, что граф <tex>G</tex> - связный==См. Соотношение <tex>p также== q + 1</tex> докажем по индукции. Утверждение очевидно для связных графов с одной и двумя вершинами. Предположим, что оно верно для графов, имеющих меньше <tex>p</tex> вершин. Если же граф <tex>G</tex> имеет <tex>p</tex> вершин, то удаление из него любого ребра делает его несвязным, в силу единственности простых цепей; более того, получаемый граф будет иметь в точности две компоненты. По предположению индукции в каждой компоненте число вершин * [[Алгоритмы на деревьях|Алгоритмы на единицу больше числа ребер. Таким образомдеревьях]]* [[Дерево поиска, общее число ребер в графе <tex>G</tex> должно равняться <tex>p-1</tex>.наивная реализация|Двоичное дерево поиска]]

3) <tex> \to </tex> 4) Предположим, что в графе <tex>G</tex> есть простой цикл длины <tex>n</tex>. Этот цикл содержит <tex>n</tex> вершин и <tex>n</tex> ребер, а для любой из <tex>p - n</tex> вершин, не принадлежащих циклу,существует инцидентное ей ребро, которое лежит на геодезической , идущей от некоторой вершины цикла. Все такие ребра попарно различны; отсюда <tex>q \ge p</tex>, т. е. пришли к противоречию.4) <tex> \to </tex> 1) Предположим граф <tex>G</tex> имеет <tex>k</tex> компонент связности, и т. к. граф ациклический, то каждая компонента связности является деревом. Ввиду того, что 1) <tex> \to </tex> 3) <tex>q = \sum_{i = 1}^k (p_i - 1) Источники информации= p - k</tex>, где <tex>p_i</tex> - количество вершин в <tex>i</tex>-й компоненте связности. Учитывая, что <tex>p = q + 1</tex>, получаем, что <tex>k = 1</tex>, т. е. <tex>G</tex> - дерево.}}

* Харари Фрэнк '''Теория графов''' = Graph theory/Пер. с англ. [[Категория: Алгоритмы и предисл. В. П. Козырева. Под ред. Г.П.Гаврилова. Изд. 2-е. — М.структуры данных]][[Категория: Едиториал УРСС, 2003. — 296 с. — ISBN 5-354-00301-6Основные определения теории графов]]