Коды Грея — различия между версиями
Zernov (обсуждение | вклад) (→Сбалансированный код Грея) |
м (rollbackEdits.php mass rollback) |
||
| (не показано 6 промежуточных версий 4 участников) | |||
| Строка 19: | Строка 19: | ||
{| border="0" | {| border="0" | ||
|align="left" colspan="4"| | |align="left" colspan="4"| | ||
| − | *<tex>\mathtt{GrayCode}</tex> {{---}} двумерный массив типа '''boolean''', в котором <tex>\mathtt{GrayCode[a, b]}</tex> {{---}} <tex>b</tex>-ый бит в <tex>a</tex>-ом коде Грея | + | *<tex>\mathtt{GrayCode}</tex> {{---}} двумерный массив типа '''boolean''', в котором <tex>\mathtt{GrayCode[a, b]}</tex> {{---}} <tex>b</tex>-ый бит в <tex>a</tex>-ом коде Грея, |
| − | *<tex>\mathtt{p}</tex> {{---}} Счетчик количества уже имеющихся кодов | + | *<tex>\mathtt{p}</tex> {{---}} Счетчик количества уже имеющихся кодов, |
| − | *<tex>\mathtt{t}</tex> {{---}} Показывает количество кодов в <tex>(a-1)</tex>-м коде Грея | + | *<tex>\mathtt{t}</tex> {{---}} Показывает количество кодов в <tex>(a-1)</tex>-м коде Грея. |
<code> | <code> | ||
buildCode(n): | buildCode(n): | ||
| Строка 61: | Строка 61: | ||
Для кода длиной <tex>1</tex> бит утверждение проверяется непосредственно. | Для кода длиной <tex>1</tex> бит утверждение проверяется непосредственно. | ||
| − | Пусть существует зеркальный двоичный код Грея <tex>M</tex> длины <tex>n</tex>, для которого выполнено, что для любого <tex>i</tex> выполняется <tex> | + | Пусть существует зеркальный двоичный код Грея <tex>M</tex> длины <tex>n</tex>, для которого выполнено, что для любого <tex>i</tex> выполняется <tex>\enspace M_i = i \oplus (\lfloor i / 2 \rfloor)</tex> |
Обозначим за <tex>L</tex> код длины <tex>n + 1</tex>, полученный из <tex>M</tex> описанным выше алгоритмом. Тогда: | Обозначим за <tex>L</tex> код длины <tex>n + 1</tex>, полученный из <tex>M</tex> описанным выше алгоритмом. Тогда: | ||
| − | Для любого <tex>x < 2^n</tex> выполняется <tex>\ | + | Для любого <tex>x < 2^n</tex> выполняется <tex>\enspace L_x = 0M_x</tex> и, по условию, равно |
<tex>L_x = 0(x_{n-1}x_{n-2} \dots x_{0} \oplus 0x_{n-1}x_{n-2} \dots x_{1})</tex> раскрыв скобки, получим новое выражение <tex>L_x</tex>: | <tex>L_x = 0(x_{n-1}x_{n-2} \dots x_{0} \oplus 0x_{n-1}x_{n-2} \dots x_{1})</tex> раскрыв скобки, получим новое выражение <tex>L_x</tex>: | ||
| Строка 73: | Строка 73: | ||
<tex>= x \oplus (\lfloor x / 2 \rfloor)</tex> | <tex>= x \oplus (\lfloor x / 2 \rfloor)</tex> | ||
| − | Для любого <tex>x \geqslant 2^n</tex> выполняется <tex>\ | + | Для любого <tex>x \geqslant 2^n</tex> выполняется <tex>\enspace L_x = 1</tex><tex>M_y</tex>, где <tex>y = 2^{n+1} - 1 - x = \neg x</tex>, то есть |
<tex>L_x = 1(\overline {x_{n-1} x_{n-2} \dots x_{0}} \oplus 0 \overline {x_{n-1} x_{n-2} \dots x_{1}})</tex> что по свойству '''xor''' (<tex>\neg x \oplus \neg y = x \oplus y</tex>) равно | <tex>L_x = 1(\overline {x_{n-1} x_{n-2} \dots x_{0}} \oplus 0 \overline {x_{n-1} x_{n-2} \dots x_{1}})</tex> что по свойству '''xor''' (<tex>\neg x \oplus \neg y = x \oplus y</tex>) равно | ||
| Строка 141: | Строка 141: | ||
Поставим в соответствие каждому <tex>i</tex>-ому биту текущего кода Грея <tex>i</tex>-ый диск (причём самому младшему биту соответствует наименьший по размеру диск, а самому старшему биту — наибольший). Поскольку на каждом шаге изменяется ровно один бит, то мы можем понимать изменение бита <tex>i</tex> как перемещение <tex>i</tex>-го диска. То есть, будем понимать переход от последовательности <tex>101</tex> к <tex>100</tex> как перемещение <tex>0</tex>-го диска на свободное место, а от <tex>010</tex> к <tex>110</tex> {{---}} как перемещение <tex>2</tex>-го диска на свободное место. | Поставим в соответствие каждому <tex>i</tex>-ому биту текущего кода Грея <tex>i</tex>-ый диск (причём самому младшему биту соответствует наименьший по размеру диск, а самому старшему биту — наибольший). Поскольку на каждом шаге изменяется ровно один бит, то мы можем понимать изменение бита <tex>i</tex> как перемещение <tex>i</tex>-го диска. То есть, будем понимать переход от последовательности <tex>101</tex> к <tex>100</tex> как перемещение <tex>0</tex>-го диска на свободное место, а от <tex>010</tex> к <tex>110</tex> {{---}} как перемещение <tex>2</tex>-го диска на свободное место. | ||
| − | Заметим, что для всех дисков, кроме наименьшего, на каждом шаге имеется ровно один вариант хода (за исключением стартовой и финальной позиций) | + | Заметим, что для всех дисков, кроме наименьшего, на каждом шаге имеется ровно один вариант хода (за исключением стартовой и финальной позиций). Для самого маленького диска всегда есть две свободные позиции, потому что он самый маленький, его можно положить сверху на любой диск. Если диск не самый маленький, то для него может быть не более одной свободной позиции. Допустим, что для него свободные две позиции. Это означает, что на двух других стержнях расположены диски размером больше, чем рассматриваемый. А так как рассматриваемый диск не самый маленький, то где-то расположен наименьший. Либо он расположен на рассматриваемом диске, тогда мы не можем переместить рассматриваемый, либо на каком-то другом, но тогда у нашего диска остаётся не более одной свободной позиции. Для наименьшего диска всегда имеется два варианта хода, однако имеется стратегия выбора хода, всегда приводящая к ответу: если <tex>n</tex> нечётно, то последовательность перемещений наименьшего диска имеет вид <tex>r_{1} \rightarrow r_{3} \rightarrow r_{2} \rightarrow r_{1} \rightarrow r_{3} \rightarrow r_{2} \rightarrow \ldots .</tex>(где <tex>r_{1}</tex> — стартовый стержень, <tex>r_{3}</tex> — финальный стержень, <tex>r_{2}</tex> — оставшийся стержень), а если <tex>n</tex> чётно, то <tex>r_{1} \rightarrow r_{2} \rightarrow r_{3} \rightarrow r_{1} \rightarrow r_{2} \rightarrow r_{3} \rightarrow \ldots.</tex> |
| − | Выбор обусловлен тем, на каком стержне окажется в конце пирамидка, решение с помощью кода Грея является следствием классического <ref>[https://en.wikipedia.org/wiki/Tower_of_Hanoi#Non-recursive_solution Wikipedia {{---}} Tower of Hanoi Non-recursive solution]</ref> | + | Выбор обусловлен тем, на каком стержне окажется в конце пирамидка, решение с помощью кода Грея является следствием классического нерекурсивного решения<ref>[https://en.wikipedia.org/wiki/Tower_of_Hanoi#Non-recursive_solution Wikipedia {{---}} Tower of Hanoi Non-recursive solution]</ref>. |
| − | |||
| − | |||
==См. Также== | ==См. Также== | ||
Текущая версия на 19:36, 4 сентября 2022
| Определение: |
| Код Грея (англ. Gray code) — такое упорядочение -ичных (обычно двоичных) векторов, что соседние вектора отличаются только в одном разряде. |
Код назван в честь Фрэнка Грея, который в 1947-ом году получил патент на "отражённый двоичный код".
Содержание
Алгоритм построения
Существует несколько видов кода Грея, самый простой из них — так называемый зеркальный двоичный код Грея. Строится он так:
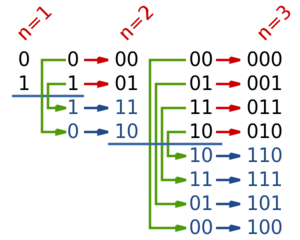
Для получения кода длины производится шагов. На первом шаге код имеет длину и состоит из двух векторов и . На каждом следующем шаге в конец списка заносятся все уже имеющиеся вектора в обратном порядке, и затем к первой половине получившихся векторов дописывается , а ко второй . С каждым шагом длина векторов увеличивается на , а их количество — вдвое. Таким образом, количество векторов длины равно
Псевдокод
buildCode(n):
GrayCode[1, n] = false
GrayCode[2, n] = true // Построение кода длины 1
p = 2
for i = 2 to n
t = p
p = p * 2
for k = (p / 2 + 1) to p
GrayCode[k] = GrayCode[t] // Отражение имеющихся кодов
GrayCode[t, n + 1 - i] = false
GrayCode[k, n + 1 - i] = true // Добавление 0 и 1 в начало
t--
return GrayCode
|
Доказательство правильности работы алгоритма
По индукции:
- на первом шаге код отвечает условиям
- предположим, что код, получившийся на -ом шаге, является кодом Грея
- тогда на шаге : первая половина кода будет корректна, так как она совпадает с кодом с шага за исключением добавленного последнего бита . Вторая половина тоже соответствует условиям, так как она является зеркальным отражением первой половины, только добавлен везде бит . На стыке: первые бит совпадают в силу зеркальности, последние различны по построению.
Таким образом, этот код — код Грея. Индукционное предположение доказано, алгоритм работает верно.
Этот алгоритм можно обобщить и для -ичных векторов. Также известен алгоритм преобразования двоичного кода в код Грея.
Существует ещё несколько видов кода Грея — сбалансированный код Грея, код Баркера-Грея, одноколейный код Грея.[1] Кроме того, коды Грея используются для упорядочения перестановок.
Явная формула для получения зеркального двоичного кода Грея
| Теорема: |
В двоичном зеркальном коде Грея -ый код может быть получен по формуле при нумерации кодов с нуля. |
| Доказательство: |
|
Для кода длиной бит утверждение проверяется непосредственно. Пусть существует зеркальный двоичный код Грея длины , для которого выполнено, что для любого выполняется Обозначим за код длины , полученный из описанным выше алгоритмом. Тогда: Для любого выполняется и, по условию, равно раскрыв скобки, получим новое выражение : что равно (второе слагаемое равно первому, побитово сдвинутого вправо.)
Для любого выполняется , где , то есть что по свойству xor () равно или (все по тому же свойству) раскрыв скобки, получим откуда получаем, зная из условия, что старший разряд равен что, аналогично первому пункту, равно Таким образом, шаг индукции доказан, следовательно, теорема верна. |
Сбалансированный код Грея
Несмотря на то, что зеркальный двоичный код Грея полезен во многих случаях, он не является оптимальным в некоторых ситуациях из-за отсутствия "однородности". В сбалансированном коде Грея, количество изменений в различных координатных позициях сделаны максимально приближенными настолько, насколько это возможно.
Чтобы показать это точнее, пусть — это -ичный полный цикл Грея, имеющий последовательность перехода , , для если в коде Грея -й и биты различны и — кол-во таких различий; отсчёты переходов (спектры) являются наборами целых чисел, определенных как для .
Код Грея является однородным или равномерно сбалансированным, если все его отсчёты переходов равны, и в этом случае у нас есть для всех . Ясно, что при , такие коды существуют только при . В противном случае, если не делится на равномерно, то можно построить сбалансированные коды Грея, где каждый отсчёт перехода либо либо .
Коды Грея также могут быть экспоненциально сбалансироваными, если все их отсчеты переходов являются смежными степеням двойки, и такие коды существуют для каждой степени двойки.
Однодорожечный код Грея
Еще один вид кода Грея — это однодорожечный код Грея, разработанный Спеддингом и уточнен Хильтгеном, Патерсоном и Брандестини.
Однодорожечный код Грея является циклическим списком уникальных двоичных кодировок длины так, что два последовательных слова отличаются ровно в одной позиции, и когда список рассматривается как матрица, каждая колонка — это циклический сдвиг первого столбца. Название происходит от их использования датчиками вращения, где количество дорожек в настоящее время измеряется с помощью контактов, в результате для каждой дорожки на выход подаётся или .
Чтобы снизить уровнень шума различных контактов не переключаясь в тот же момент времени, один датчик предпочтительно устанавливает дорожки так, что выход данных от контактов находится в коде Грея. Чтобы получить высокую угловую точность, нужно много контактов; для достижения точности хотя бы в градус нужно, по крайней мере, различных позиций на оборот, который требует минимум бит данных, и тем самым такое же количество контактов.
Не путать с цепными кодами, получаемых циклическим сдвигом.
Применение
Фрэнк Грей изобрел метод для преобразования аналоговых сигналов в отраженные двоичные кодовые группы с использованием аппарата на основе вакуумной трубки. Способ и устройство были запатентованы в 1953 году, а код получил название код Грея. "PCM трубка" — аппарат, запатентованный Греем, был сделан Раймондом У. Сирсом из (англ.) Bell Labs, работая с Греем и Уильямом М. Гудоллом.
- В технике коды Грея используются для минимизации ошибок при преобразовании аналоговых сигналов в цифровые (например, в датчиках-энкодерах [2]).
В частности, коды Грея и были открыты в связи с этим применением. (Код Грея — это код преобразования бинарных символов в -арные, такие, что двоичные последовательности, соответствующие соседним символам (сдвигам фаз), отличаются только одним битом. Обычная бинарная кодировка сравнивается с кодировкой Грея. При появлении ошибки в -арном символе наиболее вероятными являются ближайшие соседние символы, отличающиеся от переданного лишь одним битом, если используется кодировка Грея.
Таким образом, высока вероятность того, что при кодировании с помощью кода Грея в случае возникновения ошибки ошибочным будет только один из переданных битов.)
- Коды Грея используются для кодирования номера дорожек в жёстких дисках.
- Коды Грея широко применяются в теории генетических алгоритмов [3] для кодирования генетических признаков, представленных целыми числами.
- Коды Грея используются в Картах Карно[4] (при передаче в карту переменные сортируются в код Грея).
- Алгоритм модуляции 2B1Q (англ. 2 Binary 1 Quandary) [5]
- Код Грея можно использовать также и для решения следующей задачи[6]:
Задача о Ханойских башнях
| Задача: |
| Даны три стержня, на один из которых нанизаны восемь колец, причем кольца отличаются размером и лежат меньшее на большем. Задача состоит в том, чтобы перенести пирамиду из восьми колец за наименьшее число ходов на другой стержень. За один раз разрешается переносить только одно кольцо, причём нельзя класть большее кольцо на меньшее. |
Решение:
Пусть — количество дисков. Начнём с кода Грея длины , состоящего из одних нулей (т.е. ), и будем двигаться по кодам Грея (от переходить к ).
Поставим в соответствие каждому -ому биту текущего кода Грея -ый диск (причём самому младшему биту соответствует наименьший по размеру диск, а самому старшему биту — наибольший). Поскольку на каждом шаге изменяется ровно один бит, то мы можем понимать изменение бита как перемещение -го диска. То есть, будем понимать переход от последовательности к как перемещение -го диска на свободное место, а от к — как перемещение -го диска на свободное место.
Заметим, что для всех дисков, кроме наименьшего, на каждом шаге имеется ровно один вариант хода (за исключением стартовой и финальной позиций). Для самого маленького диска всегда есть две свободные позиции, потому что он самый маленький, его можно положить сверху на любой диск. Если диск не самый маленький, то для него может быть не более одной свободной позиции. Допустим, что для него свободные две позиции. Это означает, что на двух других стержнях расположены диски размером больше, чем рассматриваемый. А так как рассматриваемый диск не самый маленький, то где-то расположен наименьший. Либо он расположен на рассматриваемом диске, тогда мы не можем переместить рассматриваемый, либо на каком-то другом, но тогда у нашего диска остаётся не более одной свободной позиции. Для наименьшего диска всегда имеется два варианта хода, однако имеется стратегия выбора хода, всегда приводящая к ответу: если нечётно, то последовательность перемещений наименьшего диска имеет вид (где — стартовый стержень, — финальный стержень, — оставшийся стержень), а если чётно, то
Выбор обусловлен тем, на каком стержне окажется в конце пирамидка, решение с помощью кода Грея является следствием классического нерекурсивного решения[7].