Поиск в матрице — различия между версиями
Kolchanov (обсуждение | вклад) (→Доказательство корректности) |
м (rollbackEdits.php mass rollback) |
||
| (не показано 10 промежуточных версий 3 участников) | |||
| Строка 1: | Строка 1: | ||
{{Задача | {{Задача | ||
| − | |definition = Задана отсортированная двумерная матрица, состоящая из n строк и m столбцов. Необходимо найти расположение указанного элемента в матрице или определить, что данный элемент в матрице отсутствует. | + | |definition = Задана отсортированная двумерная матрица (матрица, для которой выполнено следующее условие: <tex> a[row][col] \leqslant a[row + 1][col], a[row][col] \leqslant a[row][col + 1] </tex> ), состоящая из <tex>n</tex> строк и <tex>m</tex> столбцов. Необходимо найти расположение указанного элемента в матрице или определить, что данный элемент в матрице отсутствует. |
}} | }} | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
[[Файл:sorted_matrix_example.png|320px|thumb|right|Пример отсортированной матрицы]] | [[Файл:sorted_matrix_example.png|320px|thumb|right|Пример отсортированной матрицы]] | ||
| Строка 16: | Строка 10: | ||
== Решение за O(n<tex>\cdot</tex>log(m)) == | == Решение за O(n<tex>\cdot</tex>log(m)) == | ||
| − | Данный способ решения использует наивное решение за <math>n \cdot m</math>, улучшенное с помощью [[Целочисленный двоичный поиск|двоичного поиска]]. Для этого в каждой строке запускается двоичный поиск. Время работы — <tex>O(n \cdot log(m))</tex>. | + | Данный способ решения использует наивное решение за <math>n \cdot m</math>, улучшенное с помощью [[Целочисленный двоичный поиск|двоичного поиска]]. Для этого в каждой строке запускается двоичный поиск. Время работы — <tex>O(n \cdot \log(m))</tex>. |
'''Замечание''' | '''Замечание''' | ||
| − | Время работы может быть улучшено до <tex>O(min(n, m) \cdot log(max(n \cdot m))</tex>. Для этого необходимо модифицировать алгоритм так, чтобы в том случае, если столбцов больше чем строк, он бы запускал двоичный поиск по строкам, если строк больше — наоборот. | + | Время работы может быть улучшено до <tex>O(\min(n, m) \cdot \log(\max(n \cdot m))</tex>. Для этого необходимо модифицировать алгоритм так, чтобы в том случае, если столбцов больше чем строк, он бы запускал двоичный поиск по строкам, если строк больше — наоборот. |
| − | Существует еще один способ оптимизации. Рассмотрим случай, когда используется двоичный поиск по строке. Достаточно очевидно, что искомое число может находится только в тех строках, где первый элемент меньше искомого, а последний — больше. Перед началом поиска можно исключить | + | Существует еще один способ оптимизации. Рассмотрим случай, когда используется двоичный поиск по строке. Достаточно очевидно, что искомое число может находится только в тех строках, где первый элемент меньше искомого, а последний — больше. Перед началом поиска можно исключить два прямоугольных участка матрицы: первый состоит из строк, у которых последний элемент меньше искомого; второй состоит из строк, у которых первый элемент больше искомого. Используя двоичный поиск, можно найти границы этих участков за <tex>O(\log(n))</tex> для столбцов и за <tex>O(\log(m))</tex> строк. |
| + | |||
| + | |||
| + | [[Файл:find13.png|320px|thumb|right|Пример поиска числа 13 в матрице]] | ||
== Решение за O(n + m) == | == Решение за O(n + m) == | ||
| − | В данном решении мы начинаем поиск из правого верхнего угла и движемся к искомому элементу. Идея алгоритма в том, что если текущий элемент меньше необходимого, то мы сдвигаемся на одну строку вниз. Если он больше, то мы сдвигаемся на одну колонку | + | В данном решении мы начинаем поиск из правого верхнего угла и движемся к искомому элементу. Идея алгоритма в том, что если текущий элемент меньше необходимого, то мы сдвигаемся на одну строку вниз. Если он больше, то мы сдвигаемся на одну колонку влево. |
| − | |||
=== Доказательство корректности === | === Доказательство корректности === | ||
| Строка 33: | Строка 29: | ||
Пусть предыдущий ход был корректным. Докажем, что следующий ход, выполненный по правилам, будет корректным. | Пусть предыдущий ход был корректным. Докажем, что следующий ход, выполненный по правилам, будет корректным. | ||
| − | Если текущий элемент меньше искомого, то | + | Если текущий элемент меньше искомого, то все ячейки левее и выше меньше, чем искомый (по определению отсортированной матрицы, все элементы левее в строке меньше текущего, а текущий меньше искомого). |
| − | Если текущий элемент больше искомого, то очевидно, что все ячейки правее и ниже больше, чем искомый. Значит, их | + | Если текущий элемент больше искомого, то очевидно, что все ячейки правее и ниже больше, чем искомый (по определению отсортированной матрицы, все элементы ниже в столбце больше текущего, а текущий больше искомого). Значит, их можно отсечь. |
В определенный момент времени алгоритм либо найдет ячейку с искомым элементом (значит, элемент найден), либо в матрице не останется тех элементов, которые не были отсечены (значит, элемента в матрице нет). | В определенный момент времени алгоритм либо найдет ячейку с искомым элементом (значит, элемент найден), либо в матрице не останется тех элементов, которые не были отсечены (значит, элемента в матрице нет). | ||
=== Код === | === Код === | ||
| − | + | '''Pair'''<'''int''', '''int'''> matrixFind('''int'''[N][M] a, '''int''' target): | |
| − | + | '''if''' (target < a[0][0] '''or''' target > a[N-1][M-1]) | |
| − | + | '''return''' (-1, -1) | |
| − | + | row = 0 | |
| − | + | col = M - 1 | |
| − | '''while''' (row <= N-1 | + | '''while''' (row <= N-1 '''and''' col >= 0) |
'''if''' (a[row][col] < target) | '''if''' (a[row][col] < target) | ||
row++ | row++ | ||
| Строка 50: | Строка 46: | ||
col-- | col-- | ||
'''else''' | '''else''' | ||
| − | '''return''' | + | '''return''' (row, col) |
| − | + | '''return''' (-1, -1) | |
| + | |||
| + | ===Оценка времени работы=== | ||
| + | |||
| + | Очевидно, что во время работы указатель сдвигается максимум на <tex>n</tex> строк и <tex>m</tex> столбцов. В этом случае время работы составляет <tex>O(n + m)</tex>. | ||
| − | [[ | + | == См. также == |
| + | * [[Целочисленный_двоичный_поиск|Целочисленный двоичный поиск]] | ||
| − | == | + | == Источники информации == |
| + | * [http://articles.leetcode.com/2010/10/searching-2d-sorted-matrix.html| Searching a 2D Sorted Matrix часть 1 на Leetcode] | ||
| + | * [http://articles.leetcode.com/2010/10/searching-2d-sorted-matrix-part-ii.html| Searching a 2D Sorted Matrix часть 2 на Leetcode] | ||
| − | + | [[Категория: Дискретная математика и алгоритмы]] | |
| + | [[Категория: Алгоритмы поиска]] | ||
Текущая версия на 19:37, 4 сентября 2022
| Задача: |
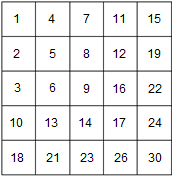
| Задана отсортированная двумерная матрица (матрица, для которой выполнено следующее условие: ), состоящая из строк и столбцов. Необходимо найти расположение указанного элемента в матрице или определить, что данный элемент в матрице отсутствует. |
Содержание
Решение за O(nm)
Для начала рассмотрим наивный алгоритм поиска элемента. В каждой строке исходной матрицы запускаем линейный поиск, если находим элемент, то возвращаем его координаты . Время работы — .
Решение за O(nlog(m))
Данный способ решения использует наивное решение за , улучшенное с помощью двоичного поиска. Для этого в каждой строке запускается двоичный поиск. Время работы — .
Замечание
Время работы может быть улучшено до . Для этого необходимо модифицировать алгоритм так, чтобы в том случае, если столбцов больше чем строк, он бы запускал двоичный поиск по строкам, если строк больше — наоборот.
Существует еще один способ оптимизации. Рассмотрим случай, когда используется двоичный поиск по строке. Достаточно очевидно, что искомое число может находится только в тех строках, где первый элемент меньше искомого, а последний — больше. Перед началом поиска можно исключить два прямоугольных участка матрицы: первый состоит из строк, у которых последний элемент меньше искомого; второй состоит из строк, у которых первый элемент больше искомого. Используя двоичный поиск, можно найти границы этих участков за для столбцов и за строк.
Решение за O(n + m)
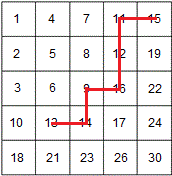
В данном решении мы начинаем поиск из правого верхнего угла и движемся к искомому элементу. Идея алгоритма в том, что если текущий элемент меньше необходимого, то мы сдвигаемся на одну строку вниз. Если он больше, то мы сдвигаемся на одну колонку влево.
Доказательство корректности
Докажем, что каждый ход в соседнюю ячейку отсекает только те столбцы или строки, которые точно не содержат искомый элемент. Назовем ход корректным, если он отсекает только те строки или колонки, в которых точно нет искомого элемента. Пусть первый ход (в правую верхнюю ячейку) корректный (он не отсек ни одной строки или столбца).
Пусть предыдущий ход был корректным. Докажем, что следующий ход, выполненный по правилам, будет корректным. Если текущий элемент меньше искомого, то все ячейки левее и выше меньше, чем искомый (по определению отсортированной матрицы, все элементы левее в строке меньше текущего, а текущий меньше искомого). Если текущий элемент больше искомого, то очевидно, что все ячейки правее и ниже больше, чем искомый (по определению отсортированной матрицы, все элементы ниже в столбце больше текущего, а текущий больше искомого). Значит, их можно отсечь.
В определенный момент времени алгоритм либо найдет ячейку с искомым элементом (значит, элемент найден), либо в матрице не останется тех элементов, которые не были отсечены (значит, элемента в матрице нет).
Код
Pair<int, int> matrixFind(int[N][M] a, int target):
if (target < a[0][0] or target > a[N-1][M-1])
return (-1, -1)
row = 0
col = M - 1
while (row <= N-1 and col >= 0)
if (a[row][col] < target)
row++
else if (a[row][col] > target)
col--
else
return (row, col)
return (-1, -1)
Оценка времени работы
Очевидно, что во время работы указатель сдвигается максимум на строк и столбцов. В этом случае время работы составляет .