Теорема Понтрягина-Куратовского — различия между версиями
м (rollbackEdits.php mass rollback) |
|||
| (не показаны 63 промежуточные версии 15 участников) | |||
| Строка 1: | Строка 1: | ||
| + | Теорему доказал в 1927 году известный советский математик Лев Семенович Понтрягин, но не опубликовал. | ||
| + | Независимо от Понтрягина в 1930 году доказательста нашел и впервые напечатал польский математик Казимир Куратовский. | ||
| + | Первые доказательства теоремы Понтрягина-Куратовского были очень сложными. Сравнительно простое доказательство нашел в 1997 г. петербургский школьник Юрий Макарычев. <br> | ||
| + | <br> | ||
| + | |||
| + | __TOC__ | ||
| + | |||
{{Теорема | {{Теорема | ||
|statement = | |statement = | ||
| − | Граф планарен тогда и только тогда, когда он не содержит подграфов, гомеоморфных <tex> K_{5} </tex> | + | Граф [[Укладка_графа_на_плоскости| планарен]] тогда и только тогда, когда он не содержит подграфов, [[Укладка графа на плоскости #def_hmp| гомеоморфных]] <tex> K_{5} </tex> или <tex> K_{3, 3} </tex> . |
|proof = | |proof = | ||
| − | + | Заметим, что из планарности графа следует планарность гомеоморфного графа и наоборот. В самом деле, пусть <tex> G_1 </tex> {{---}} плоский граф. | |
| − | + | Если добавить на нужных ребрах вершины степени <tex> 2 </tex> и удалить некотрые вершины степени <tex> 2 </tex> в <tex> G_1 </tex>, получим укладку гомеоморфного графа <tex> G_2 </tex>. Таким образом, доказательство необходимости следует из [[Непланарность_K5_и_K3,3| непланарности <tex>K_5</tex> и <tex>K_{3, 3}</tex>]]. | |
| − | + | ||
| − | От противного: пусть существует непланарный граф, который не содержит подграфов, гомеоморфных <tex> K_{5} </tex> или <tex> K_{3, 3} </tex>. Пусть <tex> G </tex> - такой граф с наименьшим возможным числом рёбер, не содержащий изолированных вершин. | + | Докажем достаточность. От противного: пусть существует непланарный граф, который не содержит подграфов, гомеоморфных <tex> K_{5} </tex> или <tex> K_{3, 3} </tex>. Пусть <tex> G </tex> {{---}} такой граф с наименьшим возможным числом рёбер, не содержащий изолированных вершин. |
| − | + | === G связен === | |
| − | Если <tex> G </tex> не связен, то его компоненты связности планарны и, следовательно, сам граф <tex> G </tex> планарен. | + | Если <tex> G </tex> не [[Отношение_связности,_компоненты_связности|связен]], то в силу минимальности <tex> G </tex> его компоненты связности планарны и, следовательно, сам граф <tex> G </tex> планарен. |
| − | + | === G {{---}} обыкновенный граф === | |
| − | В самом деле, пусть в графе <tex> G </tex> есть петля или кратное ребро <tex> e </tex>. Тогда граф <tex> G - e </tex> планарен. Добавляя ребро <tex> e </tex> к графу <tex> G - e </tex> получим, что граф <tex> G </tex> | + | В самом деле, пусть в графе <tex> G </tex> есть петля или кратное ребро <tex> e </tex>. Тогда в силу минимальности <tex> G </tex> граф <tex> G - e </tex> планарен. Добавляя ребро <tex> e </tex> к графу <tex> G - e </tex> получим, что граф <tex> G </tex> планарен. |
| − | + | === G {{---}} [[Отношение_вершинной_двусвязности|блок]] === | |
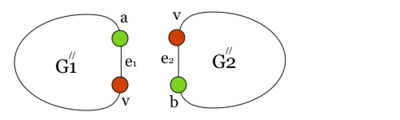
| − | Пусть, от противного, в графе есть точка сочленения <tex> v </tex>. Через <tex> G_1 </tex> обозначим подграф графа <tex> G </tex>, порождённый вершинами одной из компонент связности графа <tex> G - v</tex> и вершинной <tex> v </tex>, а через | + | Пусть, от противного, в графе есть [[Точка_сочленения,_эквивалентные_определения|точка сочленения]] <tex> v </tex>. Через <tex> G_1 </tex> обозначим подграф графа <tex> G </tex>, порождённый вершинами одной из компонент связности графа <tex> G - v</tex> и вершинной <tex> v </tex>, а через |
| − | <tex> G_2 </tex> подграф графа <tex> G </tex>, порождённый вершинами остальных компонент связности графа <tex> G - v </tex> и вершиной <tex> v </tex>. | + | <tex> G_2 </tex> подграф графа <tex> G </tex>, порождённый вершинами остальных компонент связности графа <tex> G - v </tex> и вершиной <tex> v </tex>. |
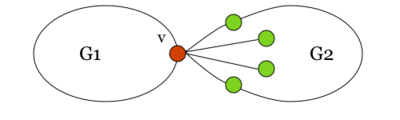
| − | [[Файл: | + | |
| − | Возьмём укладку графа <tex> G_1 </tex> на плоскости такую, что вершина <tex> v </tex> лежит на границе | + | В силу минимальности <tex> G </tex>, <tex> G_1 </tex> и <tex> G_2 </tex> {{---}} планарны. |
| − | [[Файл: | + | |
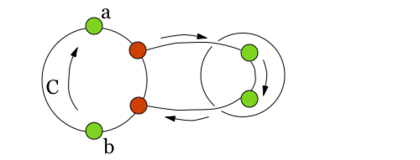
| − | Соединим два экземпляра вершины <tex> v </tex> пучком жордановых линий, не допуская лишних пересечений с укладками графов <tex> G_1 </tex> и <tex> G_2 </tex>, состоящим из такого количества линий, какова степень вершины <tex> v </tex> в графе <tex> G_2 </tex>. Далее отбросим вхождение вершины <tex> v </tex> в граф <tex> G_2 </tex>, заменяя инцидентные | + | [[Файл:New.nb.pic.1.png|400px|рис. 1]] |
| − | [[Файл: | + | |
| + | Возьмём укладку графа <tex> G_1 </tex> на плоскости такую, что вершина <tex> v </tex> лежит на границе внешней грани. Ее можно получить, взяв любую укладку <tex> G_1 </tex> на плоскости, по ней построив укладку на шаре, используя обратную стереографическую проекцию<ref> [http://en.wikipedia.org/wiki/Stereographic_projection Wikipedia {{---}} Stereographic projection] </ref>, потом повернуть сферу так, чтоб <tex> v </tex> оказалась на внешней грани стереографической проекции повернутого шара. | ||
| + | |||
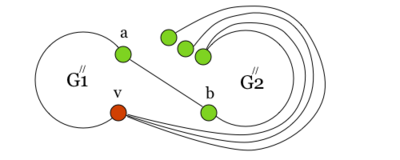
| + | Затем во внешней грани графа <tex> G_1 </tex> возьмём укладку графа <tex> G_2 </tex> такую, что вершина <tex> v </tex> будет представлена на плоскости в двух экземплярах. | ||
| + | |||
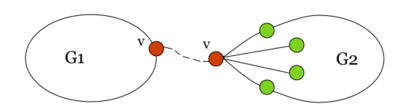
| + | [[Файл:nb.pic.2.png|400px|рис. 2]] | ||
| + | |||
| + | Соединим два экземпляра вершины <tex> v </tex> пучком жордановых линий, не допуская лишних пересечений с укладками графов <tex> G_1 </tex> и <tex> G_2 </tex>, состоящим из такого количества линий, какова степень вершины <tex> v </tex> в графе <tex> G_2 </tex>. Далее отбросим вхождение вершины <tex> v </tex> в граф <tex> G_2 </tex>, заменяя инцидентные ей рёбра на жордановы линии, полученные из линий указанного пучка и рёбер. | ||
| + | |||
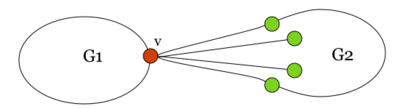
| + | [[Файл:nb.pic.3.png|400px|рис. 3]] | ||
| + | |||
Таким образом мы получили укладку графа <tex> G </tex> на плоскости, что невозможно. | Таким образом мы получили укладку графа <tex> G </tex> на плоскости, что невозможно. | ||
| − | < | + | === В G нет мостов === |
| − | Пусть <tex> e = ab </tex> - произвольное ребро графа <tex> G </tex>, <tex> G' = G - e </tex>. | + | Граф <tex> G </tex> не равен <tex> K_2 </tex> и в нем нет точек сочленения, следовательно в <tex> G </tex> нет [[Мост,_эквивалентные_определения|мостов]]. |
| + | === В G' существует цикл, содержащий вершины a и b === | ||
| + | Пусть <tex> e = ab </tex> {{---}} произвольное ребро графа <tex> G </tex>, <tex> G' = G - e </tex>. | ||
# граф <tex> G' </tex> планарен в силу минимальности графа <tex> G </tex>. | # граф <tex> G' </tex> планарен в силу минимальности графа <tex> G </tex>. | ||
# граф <tex> G' </tex> связен в силу отсутствия в графе <tex> G </tex> мостов. | # граф <tex> G' </tex> связен в силу отсутствия в графе <tex> G </tex> мостов. | ||
| − | |||
Пусть <tex> a </tex> и <tex> b </tex> лежат в одном блоке <tex> B </tex> графа <tex> G' </tex>. | Пусть <tex> a </tex> и <tex> b </tex> лежат в одном блоке <tex> B </tex> графа <tex> G' </tex>. | ||
| − | # Если <tex> |VB| | + | # Если <tex>|VB| \geqslant 3</tex>, то существует цикл графа G', содержащий вершины <tex> a </tex> и <tex> b </tex>. |
# Если <tex> |VB| = 2 </tex>, то в <tex> B </tex> имеется ребро <tex> e' = ab </tex>, но тогда в <tex> G </tex> имеются кратные рёбра <tex> e </tex> и <tex> e' </tex>, что невозможно. | # Если <tex> |VB| = 2 </tex>, то в <tex> B </tex> имеется ребро <tex> e' = ab </tex>, но тогда в <tex> G </tex> имеются кратные рёбра <tex> e </tex> и <tex> e' </tex>, что невозможно. | ||
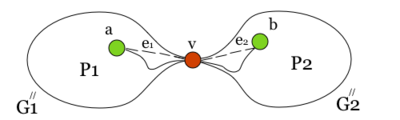
| − | # Если вершины <tex> a </tex> и <tex> b </tex> лежат в разных блоках графа <tex> G' </tex>, что существует точка сочленения <tex> v </tex>, принадлежащая любой простой (a, b)-цепи графа <tex> G' </tex>. Через <tex> G'_1 </tex> обозначим подграф графа <tex> G' </tex>, порождённый вершиной <tex> v </tex> и вершинами компоненты связности графа <tex> G' - v </tex>, содержащей <tex> a </tex>, а через <tex> G'_2 </tex> - подграф графа <tex> G' </tex>, порождённый вершиной <tex> v </tex> и вершинами остальных компонент связности графа <tEx> G' - v </tex> (в этом множестве лежит вершина <tex> b </tex>). Пусть <tex> G''_1 = G'_1 + e_1 </tex>, где <tex> | + | #Если вершины <tex> a </tex> и <tex> b </tex> лежат в разных блоках графа <tex> G' </tex>, что существует точка сочленения <tex> v </tex>, принадлежащая любой простой <tex> (a, b) </tex> {{---}} цепи графа <tex> G' </tex>. Через <tex> G'_1 </tex> обозначим подграф графа <tex> G' </tex>, порождённый вершиной <tex> v </tex> и вершинами компоненты связности графа <tex> G' - v </tex>, содержащей <tex> a </tex>, а через <tex> G'_2 </tex> {{---}} подграф графа <tex> G' </tex>, порождённый вершиной <tex> v </tex> и вершинами остальных компонент связности графа <tEx> G' - v </tex> (в этом множестве лежит вершина <tex> b </tex>). Пусть <tex> G''_1 = G'_1 + e_1 </tex>, где <tex> e_1 = vb </tex> {{---}} новое ребро. |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | [[Файл:nb.pic.4.png|400px|рис. 4]] | ||
| − | Среди всех укладок графа < | + | Заметим, что в графе <tex> G''_1 </tex> рёбер меньше, чем в графе <tex> G </tex>. Действительно, вместо ребра <tex> e </tex> в <tex> G''_1 </tex> есть ребро <tex> e_1 </tex> и часть рёбер из графа <tex> G </tex> осталась в графе <tex> G''_2 </tex>. Аналогично, в графе <tex> G''_2 </tex> рёбер меньше, чем в графе <tex> G </tex>. <br/> |
| + | Теперь в силу минимальности графа <tex> G </tex> графы <tex> G''_1 </tex> и <tex> G''_2 </tex> планарны. Возьмем укладку графа <tex> G''_1 </tex> на плоскости такую, что ребро <tex> e_1 = av </tex> лежит на границе внешней грани(ее существование доказывается аналогично существованию такой укладки для вершины графа). Во внешней грани графа <tex> G''_1 </tex> возьмем укладку графа <tex> G''_2 </tex> такую, что ребро <tex> e_2 = vb </tex> лежит па границе внешней грани. | ||
| + | |||
| + | [[Файл:nb.pic.5.png|400px|рис. 5]] | ||
| + | |||
| + | Отметим, что опять вершина <tex> v </tex> представлена на плоскости в двух экземплярах. Очевидно, добавление ребра <tex> e = ab </tex> не меняет планарности графа <tex> G''_1 U G''_2</tex>. Склеим оба вхождения вершины <tex> v </tex> точно так же, как это мы сделали в предыдущем пункте доказательства. | ||
| + | |||
| + | [[Файл:nb.pic.6.png|400px|рис. 6]] | ||
| + | |||
| + | Сотрем затем ранее добавленные ребра <tex> e_1 </tex> и <tex> e_2 </tex>. В результате мы получим укладку графа <tex> G </tex> на плоскости, что невозможно. Утверждение доказано. | ||
| + | |||
| + | ===Вспомогательные определения и утверждение об одновременно разделяющейся внутренней части=== | ||
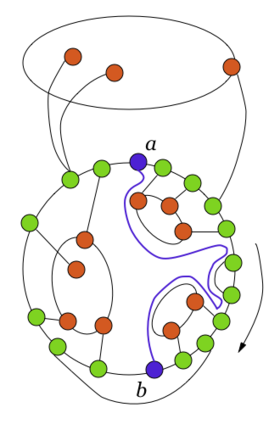
| + | Среди всех укладок графа <tex>G'</tex> на плоскости и среди всех циклов <tex>C</tex>, содержащих <tex>a</tex> и <tex>b</tex>, зафиксируем такую укладку и такой цикл, что внутри области, ограниченной циклом <tex>C</tex>, лежит максимальное возможное число граней графа <tex>G'</tex>. Зафиксируем один из обходов по циклу <tex>C</tex> (на рисунках будем рассматривать обход по часовой стрелке по циклу <tex>C</tex>). Для вершин <tex>u</tex> и <tex>v</tex> цикла <tex>C</tex> через <tex>C[u,v]</tex> будем обозначать простую <tex>(u,v)</tex> {{---}} цепь, идущую по циклу <tex>C</tex> от <tex>u</tex> до <tex>v</tex> в направлении обхода цикла. Конечно, <tex>C[u,v] \ne C[v,u]</tex>. Положим <tex>C(u,v) = C[u,v] \setminus</tex> {<tex>u,v</tex>}, т.е. <tex>C(u,v)</tex> получено из <tex>C[u,v]</tex> отбрасыванием вершин <tex>u</tex> и <tex>v</tex>. | ||
{{Определение | {{Определение | ||
|definition = | |definition = | ||
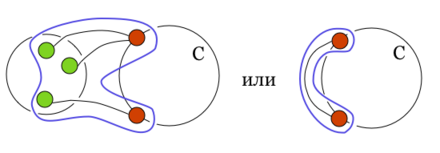
| − | Внешним графом (относительно цикла < | + | <b>Внешним графом </b> (англ. ''Outside graph'') (относительно цикла <tex>C</tex>) будем называть подграф графа <tex>G'</tex>, порождённый всеми вершинами графа <tex>G'</tex>, лежащими снаружи от цикла <tex>C</tex>. |
}} | }} | ||
{{Определение | {{Определение | ||
|definition = | |definition = | ||
| − | Внешними компонентами будем называть компоненты связности внешнего графа. | + | <b>Внешними компонентами</b> (англ. ''Outside components'') будем называть компоненты связности внешнего графа. |
}} | }} | ||
| − | В силу связности графа < | + | В силу связности графа <tex>G'</tex> для любой внешней компоненты должны существовать рёбра в <tex>G'</tex>, соединяющие её с вершинами цикла <tex>C</tex>. |
{{Определение | {{Определение | ||
|definition = | |definition = | ||
| − | Внешними частями будем называть | + | <b>Внешними частями</b> (англ. ''Outside parts'') будем называть внешние компоненты вместе со всеми рёбрами, соединяющими компоненту с вершинами цикла <tex>C</tex>, и инцидентными им вершинами , либо рёбра графа <tex>G'</tex>, лежащие снаружи от цикла <tex>C</tex> и соединяющие две вершины из <tex>C</tex>, вместе с инцидентными такому ребру вершинами. |
| − | |||
| − | |||
}} | }} | ||
| − | {{ | + | [[Файл:nb.pic.7.png|440px|рис. 7]] |
| + | {{Определение | ||
|definition = | |definition = | ||
| − | Внутренним графом (относительно цикла < | + | <b>Внутренним графом</b> (англ. ''Inside graph'') (относительно цикла <tex>C</tex>) будем называть подграф графа <tex>G'</tex>, порождённый всеми вершинами графа <tex>G'</tex>, лежащими внутри цикла <tex>C</tex>. |
}} | }} | ||
{{Определение | {{Определение | ||
|definition = | |definition = | ||
| − | Внутренними компонентами будем называть компоненты связности внутреннего графа. | + | <b>Внутренними компонентами</b> (англ. ''Inside components'') будем называть компоненты связности внутреннего графа. |
}} | }} | ||
| − | В силу связности графа < | + | В силу связности графа <tex>G'</tex> для любой внутренней компоненты должны существовать рёбра в <tex>G'</tex>, соединяющие её с вершинами цикла <tex>C</tex>. |
{{Определение | {{Определение | ||
|definition = | |definition = | ||
| − | Внутренними частями будем называть | + | <b>Внутренними частями</b> (англ. ''Inside parts'') будем называть внутренние компоненты вместе со всеми рёбрами, соединяющими компоненту с вершинами цикла <tex>C</tex>, и инцидентными им вершинами, либо рёбра графа <tex>G'</tex>, лежащие внутри цикла <tex>C</tex> и соединяющие две вершины из <tex>C</tex>, вместе с инцидентными такому ребру вершинами |
| − | |||
| − | |||
}} | }} | ||
| − | Будем говорить, что внешняя (внутренняя) часть ''встречает цикл'' < | + | Будем говорить, что внешняя (внутренняя) часть ''встречает цикл'' <tex>C</tex> в своих точках прикрепления к циклу <tex>C</tex>. |
| − | {{ | + | {{Лемма |
| + | |about=1 | ||
|statement = | |statement = | ||
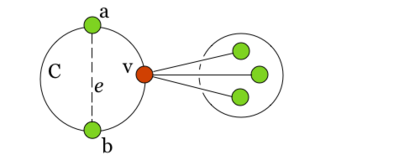
| − | Любая внешняя часть встречает цикл < | + | Любая внешняя часть встречает цикл <tex>C</tex> точно в двух точках, одна из которых лежит в <tex>C(a,b)</tex>, а другая {{---}} в <tex>C(b,a)</tex>. |
|proof = | |proof = | ||
| − | Если внешняя часть встречает цикл < | + | Если внешняя часть встречает цикл <tex>C</tex> точно в одной точке <tex>v</tex>, то <tex>v</tex> является точкой сочленения графа <tex>G</tex>, что невозможно. |
| − | Таким образом, внешняя часть встречает цикл < | + | |
| − | Итого, внешняя часть встречает цикл < | + | [[Файл:nb.pic.8.png|420px|рис. 8]] |
| + | |||
| + | Таким образом, внешняя часть встречает цикл <tex>C</tex> не менее чем в двух точках. Если внешняя часть встречает цикл <tex>C</tex> в двух точках из <tex>C[a,b]</tex> (случай <tex>C[b,a]</tex> рассматривается аналогично), то в <tex>G'</tex> имеется цикл, содержащий внутри себя больше граней, чем цикл <tex>C</tex>, и проходящий через <tex>a</tex> и <tex>b</tex>, что невозможно. | ||
| + | |||
| + | [[Файл:nb.pic.9.png|420px|рис. 9]] | ||
| + | |||
| + | Итого, внешняя часть встречает цикл <tex>C</tex> хотя бы в двух точках, никакие две из которых не лежат в <tex>C[a,b]</tex> и <tex>C[b,a]</tex>. То есть ровно одна лежит в <tex>C(a,b)</tex> и ровно одна {{---}} в <tex>C(b,a)</tex>. | ||
}} | }} | ||
{{Определение | {{Определение | ||
|definition = | |definition = | ||
| − | Ввиду | + | Ввиду леммы 1 будем говорить, что любая внешняя часть является <b><tex>(a,b)</tex> {{---}} разделяющей частью</b> (англ. ''separating part''), поскольку она встречает и <tex>C(a,b)</tex>, и <tex>C(b,a)</tex>. |
}} | }} | ||
| − | Аналогично можно ввести понятие < | + | Аналогично можно ввести понятие <tex>(a,b)</tex> {{---}} разделяющей внутренней части. Заметим, что внутренняя часть может встречать цикл <tex>C</tex>, вообще говоря, более чем в двух точках, но не менее чем в двух точках. |
| − | {{ | + | {{Лемма |
| + | |about=2 | ||
|statement = | |statement = | ||
| − | Существует хотя бы одна < | + | Существует хотя бы одна <tex>(a,b)</tex> {{---}} разделяющая внутренняя часть. |
|proof = | |proof = | ||
| − | Пусть, от противного, таких частей нет. Тогда, выходя из < | + | Пусть, от противного, таких частей нет. Тогда, выходя из <tex>a</tex> внутри области, ограниченной <tex>C</tex>, и двигаясь вблизи от <tex>C</tex> по направлению обхода <tex>C</tex> и вблизи от встречающихся внутренних частей, можно уложить ребро <tex>e = ab</tex> внутри цикла <tex>C</tex>, т.е. <tex>G</tex> {{---}} планарный граф, что невозможно. |
| + | |||
| + | [[Файл:nb.pic.10.png|280px|рис. 10]] | ||
| + | |||
}} | }} | ||
| − | {{ | + | {{Лемма |
| + | |about=3 | ||
|statement = | |statement = | ||
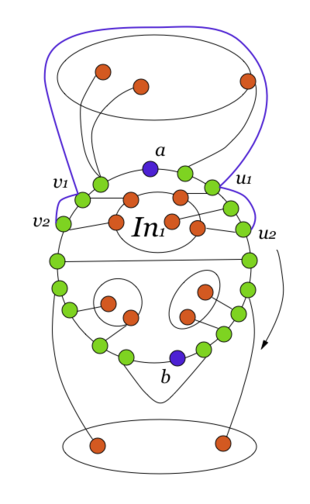
| − | Существует внешняя часть, встречающая < | + | Существует внешняя часть, встречающая <tex>C(a,b)</tex> в точке <tex>c</tex> и <tex>C(b,a)</tex> {{---}} в точке <tex>d</tex>, для которой найдётся внутренняя часть, являющаяся одновременно <tex>(a,b)</tex> {{---}} разделяющей и <tex>(c,d)</tex> {{---}} разделяющей. <br> |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | [[Файл:nb.pic.11.png|240px|рис. 11]] | |
| − | |||
| − | [[Файл: | ||
| − | |||
| − | 1 | + | |proof = |
| − | + | Пусть, от противного, лемма 3 неверна. Упорядочим <tex>(a,b)</tex> {{---}} разделяющие внутренние части в порядке их прикрепления к циклу <tex>C</tex> при движении по циклу от <tex>a</tex> до <tex>b</tex> и обозначим их соответственно через <tex>In_{1},In_{2},\dots</tex> Пусть <tex>u_{1}</tex> и <tex>u_{2}</tex> {{---}} первая и последняя вершины из <tex>C(a,b)</tex>, в которых <tex>In_{1}</tex> встречает цикл <tex>C</tex>, а <tex>v_{1}</tex> и <tex>v_{2}</tex> {{---}} первая и последняя вершины из <tex>C(b,a)</tex>, в которых <tex>In_{1}</tex> встречает цикл <tex>C</tex> (возможно, вообще говоря, <tex>u_{1} = u_{2}</tex> или <tex>v_{1} = v_{2}</tex>). Поскольку лемма 3 неверна, для любой внешней части обе её вершины, в которых она встречает <tex>C</tex>, лежат либо на <tex>C[v_{2},u_{1}]</tex>, либо на <tex>C[u_{2},v_{1}]</tex>. Тогда снаружи цикла <tex>C</tex> можно провести жорданову кривую <tex>P</tex>, не пересекая рёбер графа <tex>G'</tex>, соединяющую <tex>v_{2}</tex> с <tex>u_{1}</tex>. | |
| − | + | [[Файл:nb.pic.12.png|310px|рис. 12]] | |
| − | |||
| − | |||
| − | 2 | + | Поскольку на участках <tex>C(u_{1},u_{2})</tex> и <tex>C(v_{1},v_{2})</tex> нет точек прикрепления внешних частей, используя жорданову кривую <tex>P</tex>, внутреннюю часть <tex>In_{1}</tex> можно перебросить ("вывернуть" наружу от цикла <tex>C</tex>) во внешнюю область цикла <tex>C</tex>, т.е. уложить её снаружи от цикла <tex>C</tex> и сделать её внешней частью. |
| + | Аналогично все остальные <tex>(a,b)</tex> {{---}} разделяющие внутренние части можно перебросить во внешнюю область от цикла <tex>C</tex>. После этого точно так же, как в доказательстве леммы 2, ребро <tex>e = ab</tex> можно уложить внутри цикла <tex>C</tex>, так как не останется <tex>(a,b)</tex> {{---}} разделяющих внутренних частей. Следовательно, мы получим укладку графа <tex>G</tex>, что невозможно. | ||
| + | }} | ||
| − | |||
| − | |||
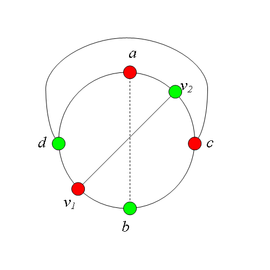
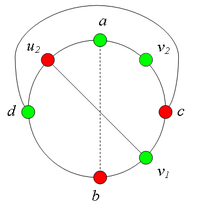
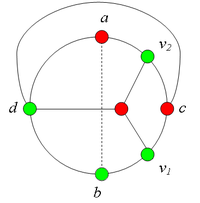
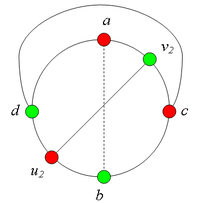
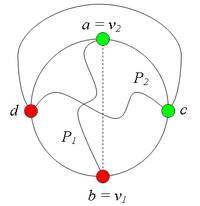
| − | + | == Разбор случаев взаимного положения вершин ''a, b, c, d, u1, u2, v1, v2'' == | |
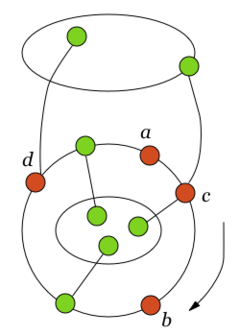
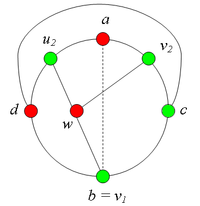
| − | + | * Пусть пара вершин <tex>\ v_1 </tex> и <tex>\ v_2 </tex> <b> является </b> <tex>(a, b)</tex> {{---}} разделяющей. <br> | |
| + | *: Тогда, в частности, <tex>v_2 \ne a</tex> и <tex> v_1 \ne b</tex>. | ||
| + | *: В этом случае граф <tex>G</tex> содержит подграф, гомеоморфный <tex>\ K_{3,3} </tex> (отметим, что в <tex> In </tex> существует простая <tex>(v_1, v_2)</tex> {{---}} цепь). | ||
| − | + | ;: [[Файл:Case_1.png|270px|рис. 7.1]] | |
| − | |||
| − | < | + | * Пусть пара вершин <tex>v_1</tex> и <tex>v_2</tex> <b> не является </b> <tex>(a, b)</tex> {{---}} разделяющей. <br> |
| − | [[Файл:Сase_2.1.png| | + | *: Тогда <tex>v_1, v_2</tex> лежат на <tex>C[a, b]</tex> или на <tex>C[b, a]</tex>. |
| − | [[Файл:Сase_2.1.1.png| | + | *: Без ограничения общности будет считать, что <tex>v_1</tex> и <tex>v_2</tex> лежат на <tex>C[a, b]</tex>.<br> |
| − | [[Файл:Сase_2. | + | *: <br> |
| − | [[Файл:Сase_2. | + | *# <b>Пусть <tex>v_1</tex> и <tex>v_2</tex> лежат на <tex>C(a, b)</tex>, т.е. <tex>v_1 \ne b</tex> и <tex>v_2 \ne a</tex>. <br></b> |
| − | </ | + | *## Пусть <tex>u_2</tex> лежит на <tex>C(d, a)</tex>.<br> |
| + | *##: Тогда в графе <tex>G</tex> имеется подграф, гомеоморфный <tex>K_{3,3}</tex>. | ||
| + | *##: [[Файл:Сase_2.1.1.png|200px|рис. 7.3]] | ||
| + | *## Пусть <tex>u_2 = d</tex>.<br> | ||
| + | *##:Тогда во внешней части <tex>In</tex> имеется вершина <tex>w</tex> и три простые цепи от <tex>w</tex> соответственно до <tex>d, v_1, v_2</tex>, которые в качестве общей точки имеют только точку <tex>w</tex>. | ||
| + | *##:В этом случае в графе <tex>G</tex> имеется подграф, гомеоморфный <tex>K_{3,3}</tex>.<br> | ||
| + | *##:[[Файл:Сase_2.1.2.png|200px|рис. 7.4]] | ||
| + | *## Пусть <tex>u_2</tex> лежит на <tex>C(b, d)</tex>.<br> | ||
| + | *##:Тогда в графе <tex>G</tex> есть подграф, гомеоморфный <tex>K_{3,3}</tex>.<br> | ||
| + | *##:[[Файл:Сase_2.1.3.png|200px|рис. 7.5]] | ||
| + | *#:<br> | ||
| + | *#:Теперь рассмотрим случаи (2 и 3), когда хотя бы одна из вершин <tex>v_1</tex> и <tex>v_2</tex> не лежит на <tex>С(a, b)</tex>. | ||
| + | *#:Без ограничения общности будем считать, что это вершина <tex>v_1</tex>, т.е <tex>v_1 = b</tex>(поскольку <tex>v_1</tex> лежит на <tex>C[a, b]</tex>).<br> | ||
| + | *#:<br> | ||
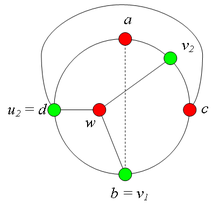
| + | *# <b> Пусть <tex>v_2 \ne a</tex>.<br> </b> | ||
| + | *##: Пусть <tex>u_2</tex> лежит на <tex>C(d, a)</tex>.<br> | ||
| + | *##: Тогда в графе <tex>G</tex> есть пограф, гомеоморфный <tex>K_{3,3}</tex>.<br> | ||
| + | *##:[[Файл:Сase_2.2.1.png|200px|рис. 7.6]] | ||
| + | *## Пусть <tex>u_2 = d</tex>.<br> | ||
| + | *##:Тогда в графе <tex>G</tex> имеется подграф, гомеоморфный <tex>K_{3,3}</tex>.<br> | ||
| + | *##:[[Файл:Сase_2.2.2.png|220px|рис. 7.7]] | ||
| + | *## Пусть <tex>u_2</tex> лежит на <tex>C(b, d)</tex>.<br> | ||
| + | *##:Тогда в графе <tex>G</tex> имеется подграф, гомеоморфный <tex>K_{3,3}</tex>. <br> | ||
| + | *##:[[Файл:Сase_2.2.3.png|200px|рис. 7.8]] | ||
| + | *#:<br> | ||
| + | *#:<br> | ||
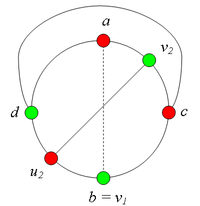
| + | *# <b> Пусть <tex>v_2 = a</tex>.<br> </b> | ||
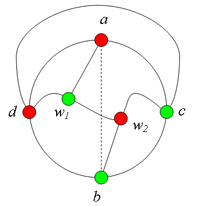
| + | *#:[[Файл:Сase_2.3(a).png|200px|рис. 7.9]] | ||
| + | *#:Рассмотрим теперь пару вершин <tex>u_1</tex> и <tex>u_2</tex>. | ||
| + | *#:Будем считать, что <tex>u_1 = c</tex> и <tex>u_2 = d</tex>, поскольку все другие случаи расположения вершин <tex>u_1</tex> и <tex>u_2</tex> так же, как были рассмотрены все случаи расположения <tex>v_1</tex> и <tex>v_2</tex>. | ||
| + | *#:Пусть <tex>P_1</tex> и <tex>P_2</tex> {{---}} соответственно кратчайшие простые <tex>(a, b)</tex> {{---}} цепь и <tex>(c, d)</tex>-цепь по внутренней части <tex>In</tex>. | ||
| + | *#:[[Файл:Сase_2.3(b).png|200px|рис. 7.10]] | ||
| + | *#:Заметим, что <tex>P_1</tex> и <tex>P_2</tex> имеют общую точку.<br> | ||
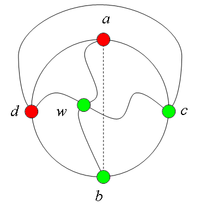
| + | *#: <br> | ||
| + | *## Пусть цепи <tex>P_1</tex> и <tex>P_2</tex> имеют более одной общей точки.<br> | ||
| + | *##: Тогда в графе <tex>G</tex> есть подграф, гомеоморфный <tex>K_{3,3}</tex>.<br> | ||
| + | *##: [[Файл:Сase_2.3.1.png|200px|рис. 7.11]] | ||
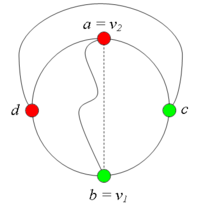
| + | *## Пусть цепи <tex>P_1</tex> и <tex>P_2</tex> имеют точно одну общую точку <tex>w</tex>.<br> | ||
| + | *##: Тогда в графе <tex>G</tex> есть подграф, гомеоморфный <tex>K_5</tex>.<br> | ||
| + | *##: [[Файл:Сase_2.3.2.png|200px|рис. 7.12]] | ||
| − | + | Таким образом, доказано, что в графе <tex>G</tex> имеется подграф, гомеоморфный <tex>K_{3,3}</tex> или <tex>K_5</tex>, что противоречит нашему первому предположению.<br> | |
| + | }} | ||
| − | + | == См. также == | |
| + | * [[Двойственный граф планарного графа]] | ||
| + | * [[Теорема Фари]] | ||
| − | + | == Примечания == | |
| − | + | <references /> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | == | + | ==Источники информации== |
| − | * Асанов М | + | * [https://ru.wikipedia.org/wiki/Планарный_граф Википедия {{---}} Планарный граф] |
| + | * [http://en.wikipedia.org/wiki/Kuratowski's_theorem Wikipedia {{---}} Kuratowski's theorem] | ||
| + | * [http://acm.math.spbu.ru/~sk1/download/books/TheoremKuratowski.pdf "Вокруг критерия Куратовского планарности графов" (стр. 118)] | ||
| + | * Асанов М., Баранский В., Расин В. {{---}} Дискретная математика {{---}} Графы, матроиды, алгоритмы | ||
[[Категория: Алгоритмы и структуры данных]] | [[Категория: Алгоритмы и структуры данных]] | ||
[[Категория: Укладки графов ]] | [[Категория: Укладки графов ]] | ||
Текущая версия на 19:38, 4 сентября 2022
Теорему доказал в 1927 году известный советский математик Лев Семенович Понтрягин, но не опубликовал.
Независимо от Понтрягина в 1930 году доказательста нашел и впервые напечатал польский математик Казимир Куратовский.
Первые доказательства теоремы Понтрягина-Куратовского были очень сложными. Сравнительно простое доказательство нашел в 1997 г. петербургский школьник Юрий Макарычев.
Содержание
- 1 G связен
- 2 G — обыкновенный граф
- 3 G — блок
- 4 В G нет мостов
- 5 В G' существует цикл, содержащий вершины a и b
- 6 Вспомогательные определения и утверждение об одновременно разделяющейся внутренней части
- 7 Разбор случаев взаимного положения вершин a, b, c, d, u1, u2, v1, v2
- 8 См. также
- 9 Примечания
- 10 Источники информации
| Теорема: | ||||||||||||||||||||||||||
Граф планарен тогда и только тогда, когда он не содержит подграфов, гомеоморфных или . | ||||||||||||||||||||||||||
| Доказательство: | ||||||||||||||||||||||||||
|
Заметим, что из планарности графа следует планарность гомеоморфного графа и наоборот. В самом деле, пусть — плоский граф. Если добавить на нужных ребрах вершины степени и удалить некотрые вершины степени в , получим укладку гомеоморфного графа . Таким образом, доказательство необходимости следует из непланарности и . Докажем достаточность. От противного: пусть существует непланарный граф, который не содержит подграфов, гомеоморфных или . Пусть — такой граф с наименьшим возможным числом рёбер, не содержащий изолированных вершин. G связенЕсли не связен, то в силу минимальности его компоненты связности планарны и, следовательно, сам граф планарен. G — обыкновенный графВ самом деле, пусть в графе есть петля или кратное ребро . Тогда в силу минимальности граф планарен. Добавляя ребро к графу получим, что граф планарен. G — блокПусть, от противного, в графе есть точка сочленения . Через обозначим подграф графа , порождённый вершинами одной из компонент связности графа и вершинной , а через подграф графа , порождённый вершинами остальных компонент связности графа и вершиной . В силу минимальности , и — планарны. Возьмём укладку графа на плоскости такую, что вершина лежит на границе внешней грани. Ее можно получить, взяв любую укладку на плоскости, по ней построив укладку на шаре, используя обратную стереографическую проекцию[1], потом повернуть сферу так, чтоб оказалась на внешней грани стереографической проекции повернутого шара. Затем во внешней грани графа возьмём укладку графа такую, что вершина будет представлена на плоскости в двух экземплярах. Соединим два экземпляра вершины пучком жордановых линий, не допуская лишних пересечений с укладками графов и , состоящим из такого количества линий, какова степень вершины в графе . Далее отбросим вхождение вершины в граф , заменяя инцидентные ей рёбра на жордановы линии, полученные из линий указанного пучка и рёбер. Таким образом мы получили укладку графа на плоскости, что невозможно. В G нет мостовГраф не равен и в нем нет точек сочленения, следовательно в нет мостов. В G' существует цикл, содержащий вершины a и bПусть — произвольное ребро графа , .
Пусть и лежат в одном блоке графа .
Заметим, что в графе рёбер меньше, чем в графе . Действительно, вместо ребра в есть ребро и часть рёбер из графа осталась в графе . Аналогично, в графе рёбер меньше, чем в графе . Отметим, что опять вершина представлена на плоскости в двух экземплярах. Очевидно, добавление ребра не меняет планарности графа . Склеим оба вхождения вершины точно так же, как это мы сделали в предыдущем пункте доказательства. Сотрем затем ранее добавленные ребра и . В результате мы получим укладку графа на плоскости, что невозможно. Утверждение доказано. Вспомогательные определения и утверждение об одновременно разделяющейся внутренней частиСреди всех укладок графа на плоскости и среди всех циклов , содержащих и , зафиксируем такую укладку и такой цикл, что внутри области, ограниченной циклом , лежит максимальное возможное число граней графа . Зафиксируем один из обходов по циклу (на рисунках будем рассматривать обход по часовой стрелке по циклу ). Для вершин и цикла через будем обозначать простую — цепь, идущую по циклу от до в направлении обхода цикла. Конечно, . Положим {}, т.е. получено из отбрасыванием вершин и .
В силу связности графа для любой внешней компоненты должны существовать рёбра в , соединяющие её с вершинами цикла .
В силу связности графа для любой внутренней компоненты должны существовать рёбра в , соединяющие её с вершинами цикла .
Будем говорить, что внешняя (внутренняя) часть встречает цикл в своих точках прикрепления к циклу .
Аналогично можно ввести понятие — разделяющей внутренней части. Заметим, что внутренняя часть может встречать цикл , вообще говоря, более чем в двух точках, но не менее чем в двух точках.
Разбор случаев взаимного положения вершин a, b, c, d, u1, u2, v1, v2
| ||||||||||||||||||||||||||
См. также
Примечания
Источники информации
- Википедия — Планарный граф
- Wikipedia — Kuratowski's theorem
- "Вокруг критерия Куратовского планарности графов" (стр. 118)
- Асанов М., Баранский В., Расин В. — Дискретная математика — Графы, матроиды, алгоритмы