Дерево Уоллеса

Текущая версия на 19:39, 4 сентября 2022

Дерево Уоллеса (англ. Wallace tree) — схема для умножения двух чисел. Время работы [math]O(\log n)[/math].

Содержание

1 Принцип работы
- 1.1 Дерево Уоллеса
- 1.2 Элемент 3→2
2 Схемная сложность
3 См. также
4 Источники информации

Принцип работы

Иллюстрация работы дерева для суммирования 9 чисел

Для получения произведения, воспользуемся методом, напоминающим умножение «в столбик»: распишем произведение в сумму [math]n[/math] чисел (как в матричном умножителе).

Однако, в отличие от матричного умножителя, дерево Уоллеса складывает все числа не последовательно, а с помощью специального элемента(назовём его [math]3\to2[/math]), преобразующего [math]3[/math] числа [math]x[/math], [math]y[/math] и [math] z [/math] в числа [math]a[/math] и [math]b[/math] такие, что [math]x + y + z = a + b[/math].

С помощью этого элемента на каждом шаге производятся следующие операции:

Берутся тройки чисел [math](x_1, x_2, x_3)[/math], [math](x_4, x_5, x_6)[/math], [math]\ldots[/math]
Для каждой тройки применяется элемент [math]3\to2[/math].
Повторяются пункты 1 и 2 пока не осталось [math]2[/math] числа.
Оставшиеся [math]2[/math] числа складываются с помощью двоичного каскадного сумматора.

На выходе имеем число, которое равно сумме чисел на всех входах.

Элемент 3→2

Для того, чтобы представить сумму трёх чисел с помощью двух чисел, воспользуемся полным сумматором. Для каждого [math]i[/math] направим [math]x_i[/math], [math]y_i[/math] и [math]z_i[/math] на вход полного сумматора. Тогда младший бит сумматора будет [math]i[/math]-ым битом первого числа, а старший — [math](i + 1)[/math]-ым второго.

Очевидно, полученные числа в сумме дают [math]x + y + z[/math].

На иллюстрации изображён элемент [math]3\to2[/math] для четырёхбитных чисел, в верхнем прямоугольнике изображены четыре полных сумматора, выходы которых и являются разрядами результатов.

Поскольку все полные сумматоры работают параллельно (выходы на каждом из них зависят только от собственных входов), то глубина такой схемы есть константа (не зависит от количества бит).

Схемная сложность

Определим количество элементов и глубину схемы для умножения двух чисел из [math]n[/math] бит.

Каждый элемент [math]3\to2[/math] имеет глубину [math]O(1)[/math] и размер [math]O(n)[/math].

Подсчитаем количество элементов [math]3\to2[/math]. На каждом шаге количество чисел, которые нужно просуммировать, уменьшается в полтора раза. Тогда глубина дерева будет равна [math]\log_{\frac{3}{2}}n[/math], и в нём будет элементов [math]3\to2[/math]. Обозначим за [math]size[/math] общее количество элементов в цепи; за [math]size_{3\to2}[/math] количество элементов [math]3\to2[/math]; за [math]size_{sum}[/math] количество элементов двоичного каскадного сумматора в схеме; за [math]depth[/math] глубину схемы; за [math]depth_{3\to2}[/math] глубину каждого из элементов [math]3\to2[/math]; за [math]depth_{sum}[/math] глубину каждого из элементов двоичного каскадного сумматора. Тогда общая сложность равна

См. также

Источники информации

Кормен, Т., Лейзерсон, Ч., Ривест, Р. Алгоритмы: построение и анализ — 960 с. — ISBN 5-900916-37-5

@@ Строка 1: / Строка 1: @@
-==Это что?==
+'''Дерево Уоллеса''' (англ. ''Wallace tree'') {{---}} [[Реализация булевой функции схемой из функциональных элементов|схема]] для умножения двух чисел. Время работы <tex>O(\log n)</tex>.
-Дерево Уоллеса --- схема для умножения двух чисел.
+==Принцип работы==
+===Дерево Уоллеса===
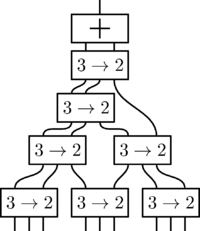
+[[file:wallace_tree.png|thumb|200px|Иллюстрация работы дерева для суммирования 9 чисел]]
-==Как оно работает(макро)?==
+Для получения произведения, воспользуемся методом, напоминающим умножение «в столбик»: распишем произведение в сумму <tex>n</tex>
+чисел (как в [[Матричный умножитель|матричном умножителе]]).
-[[file:wallace_tree.png|thumb|200px|Оно самое]]
+Однако, в отличие от [[Матричный умножитель|матричного умножителя]], дерево Уоллеса складывает все числа не последовательно, а с помощью специального элемента(назовём его <tex>3\to2</tex>), преобразующего <tex>3</tex> числа <tex>x</tex>, <tex>y</tex> и <tex> z </tex> в числа <tex>a</tex> и <tex>b</tex> такие, что <tex>x + y + z = a + b</tex>.
-В отличие от ещё одной схемы для умножения --- [[Матричный умножитель|матричного умножителя]], дерево Уоллеса не складывает все числа последовательно, а с помощью специального элемента(назовём его <math>3\to2</math>) преобразует 3 числа <math>x, y</math> и <math> z </math> в числа <math>a</math> и <math>b</math> такие, что <math>x + y + z = a + b</math>.
 С помощью этого элемента на каждом шаге производятся следующие операции:
-# Берутся тройки чисел <math>(x_1, x_2, x_3)</math>, <math>(x_4, x_5, x_6)</math> <math>\ldots</math>. При этом какие-то числа могут остаться.
+# Берутся тройки чисел <tex>(x_1, x_2, x_3)</tex>, <tex>(x_4, x_5, x_6)</tex>, <tex>\ldots</tex>
-# Для каждой тройки применяется элемент <math>3\to2</math>.
+# Для каждой тройки применяется элемент <tex>3\to2</tex>.
-# Повторять пункты 1 и 2 пока не осталось 2 числа.
+# Повторяются пункты 1 и 2 пока не осталось <tex>2</tex> числа.
-# Оставшиеся 2 числа складываются с помощью [[Двоичный каскадный сумматор|двоичного каскадного сумматора]].
+# Оставшиеся <tex>2</tex> числа складываются с помощью [[Двоичный каскадный сумматор|двоичного каскадного сумматора]].
 На выходе имеем число, которое равно сумме чисел на всех входах.
-==Как оно работает(микро)?==
+===Элемент 3→2===
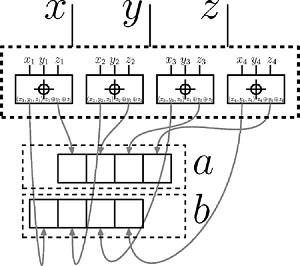
-[[file:3→2.png|thumb|200px|Элемент 3→2]]
+[[file:3v2.png|thumb|300px|Элемент 3→2]]
-Теперь о том, как устроен элемент <math>3\to2</math>.
+Для того, чтобы представить сумму трёх чисел с помощью двух чисел, воспользуемся полным сумматором. Для каждого <tex>i</tex> направим <tex>x_i</tex>, <tex>y_i</tex> и <tex>z_i</tex> на вход полного сумматора. Тогда младший бит сумматора будет <tex>i</tex>-ым битом первого числа, а старший {{---}} <tex>(i + 1)</tex>-ым второго.
+Очевидно, полученные числа в сумме дают <tex>x + y + z</tex>.
+На иллюстрации изображён элемент <tex>3\to2</tex> для четырёхбитных чисел, в верхнем прямоугольнике изображены четыре полных сумматора, выходы которых и являются разрядами результатов.
-Для построения элемента <math>3\to2</math> нам потребуется элемент, который умеет складывать 3 бита и возвращать 2 бита результата.
+Поскольку все полные сумматоры работают параллельно (выходы на каждом из них зависят только от собственных входов), то глубина такой схемы есть константа (не зависит от количества бит).
-Основная идея реализации --- отдельная обработка переносов и остатков.
-Тогда первое число ответа <math>a</math> может быть получена так:
+==Схемная сложность==
-<math>a_i = x_i \vee y_i \vee z_i</math> ,
-где <math>x</math>, <math>y</math> и <math>z</math> --- входные числа, а <math>x_i</math>, <math>y_i</math> и <math>z_i</math> --- соответствующие их <math>i</math>-е биты.
-Второе же число <math>b</math> можно получить так:
+Определим количество элементов и глубину схемы для умножения двух чисел из <tex>n</tex> бит.
-<math> \begin{cases}
-b_0 & = 0\\
-b_{i + 1} & = \langle x_i, y_i, z_i \rangle
-\end{cases}</math> ,
-где <math>\langle x, y, z\rangle</math> --- функция медианы(она же "голосование 2 из 3"). С помощью этой функции считается перенос.
-Очевидно, полученные числа <math>a</math> и <math>b</math> дадут в сумме <math>x + y + z</math>
+Каждый элемент <tex>3\to2</tex> имеет глубину <tex>O(1)</tex> и размер <tex>O(n)</tex>.
-==А чем оно лучше матричного умножителя?==
+Подсчитаем количество элементов <tex>3\to2</tex>. На каждом шаге количество чисел, которые нужно просуммировать, уменьшается в полтора раза. Тогда глубина дерева будет равна <tex>\log_{\frac{3}{2}}n</tex>, и в нём будет <tex> n + \dfrac{2}{3} n + \left(\dfrac{2}{3}\right)^2n + \ldots = O(n)</tex> элементов <tex>3\to2</tex>. Обозначим за <tex>size</tex> общее количество элементов в цепи; за <tex>size_{3\to2}</tex> количество элементов <tex>3\to2</tex>; за <tex>size_{sum}</tex> количество элементов двоичного каскадного сумматора в схеме; за <tex>depth</tex> глубину схемы; за <tex>depth_{3\to2}</tex> глубину каждого из элементов <tex>3\to2</tex>; за <tex>depth_{sum}</tex> глубину каждого из элементов двоичного каскадного сумматора.
+Тогда общая сложность равна
-Теперь подсчитаем схемную сложность этого элемента.
+<tex>depth = depth_{3\to2} \cdot \log_{3/2}n + depth_{sum} = O(\log n)</tex>
-Каждый элемент <math>3\to2</math> имеет глубину <math>O(1)</math> и размер <math>O(n)</math>.
+<tex>size = size_{3\to2} \cdot O(n) + size_{sum} = O(n^2) </tex>
-Теперь разберёмся, сколько в этой схеме элементов <math>3\to2</math>. На каждом шаге количество чисел, которые нужно просуммировать, уменьшается на <math>1/3</math>. Тогда глубина дерева будет равна <math>\log_{3/2}n<math>, и в нём будет <math>n + \frac23n + \left(\frac23\right)^2n + \ldots = O(n)</math> элементов <math>3\to2</math>.
+== См. также ==
-Тогда общая сложность равна
+* [[Матричный умножитель]]
+* [[Сумматор]]
+* [[Каскадный сумматор]]
+* [[Двоичный каскадный сумматор]]
+== Источники информации==
+* Кормен, Т., Лейзерсон, Ч., Ривест, Р. Алгоритмы: построение и анализ — 960 с. — ISBN 5-900916-37-5
-<math>depth = depth_{3\to2} \cdot \log_{3/2}n + depth_{sum} = O(\log n)</math>
+[[Категория: Дискретная математика и алгоритмы]]
-<math>size = size_{3\to2} \cdot O(n) + size_{sum} = O(n^2) </math>
+[[Категория: Схемы из функциональных элементов ]]

Дерево Уоллеса — различия между версиями

Текущая версия на 19:39, 4 сентября 2022

Содержание

Принцип работы