Сумма Минковского (определение, вычисление) — различия между версиями
Melnik (обсуждение | вклад) |
м (rollbackEdits.php mass rollback) |
||
| (не показано 6 промежуточных версий 4 участников) | |||
| Строка 1: | Строка 1: | ||
| − | |||
| − | |||
== Описание == | == Описание == | ||
| − | |||
{|align="center" | {|align="center" | ||
|-valign="top" | |-valign="top" | ||
| Строка 38: | Строка 35: | ||
Пусть заданы две выпуклые фигуры <tex>P</tex> и <tex>R</tex>, с числом вершин <tex>n</tex> и <tex>m</tex> соответственно. Тогда суммой Минковского <tex>P \oplus R</tex> является выпуклая фигура с не более чем <tex>m + n</tex> вершинами. | Пусть заданы две выпуклые фигуры <tex>P</tex> и <tex>R</tex>, с числом вершин <tex>n</tex> и <tex>m</tex> соответственно. Тогда суммой Минковского <tex>P \oplus R</tex> является выпуклая фигура с не более чем <tex>m + n</tex> вершинами. | ||
|proof= | |proof= | ||
| − | [[Файл:minkowski_extreme.png | right | | + | [[Файл:minkowski_extreme.png | right | 350px]] |
Для начала заметим, что любая крайняя точка в направлении вектора <tex>\vec{d}</tex> есть сумма крайних точек фигур в этом направлении. Убедиться в этом можно спроецировав обе фигуры на вектор <tex>\vec{d}</tex>. | Для начала заметим, что любая крайняя точка в направлении вектора <tex>\vec{d}</tex> есть сумма крайних точек фигур в этом направлении. Убедиться в этом можно спроецировав обе фигуры на вектор <tex>\vec{d}</tex>. | ||
| Строка 44: | Строка 41: | ||
}} | }} | ||
| − | == | + | == Псевдокод == |
i = j = 0 | i = j = 0 | ||
| − | V[n] = V[0], V[n+1] = V[1], W[ | + | V[n] = V[0], V[n+1] = V[1], W[m] = W[0], W[m+1] = W[1] |
while i < n or j < m do | while i < n or j < m do | ||
add V[i]+W[j] to answer | add V[i]+W[j] to answer | ||
| Строка 75: | Строка 72: | ||
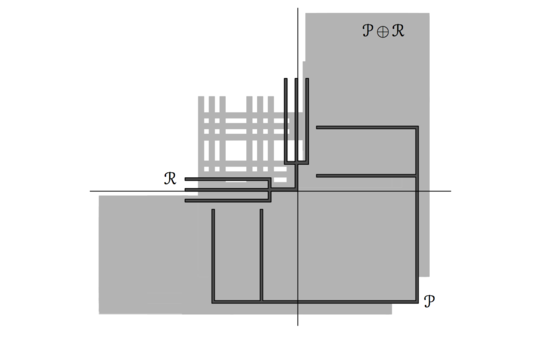
|[[Файл:minkowski_hard_example.png | thumb | 550px | Пример суммы Минковского с O(n<sup>2</sup>m<sup>2</sup>) вершинами]] | |[[Файл:minkowski_hard_example.png | thumb | 550px | Пример суммы Минковского с O(n<sup>2</sup>m<sup>2</sup>) вершинами]] | ||
|} | |} | ||
| + | |||
| + | == Ссылки == | ||
| + | * [https://en.wikipedia.org/wiki/Minkowski_addition Английская википедия] | ||
| + | * de Berg, van Kreveld, Overmars, Schwarzkopf "Computational Geometry Algorithms and Applications", p. 290 | ||
Текущая версия на 19:39, 4 сентября 2022
Содержание
Описание
| Определение: |
| Суммой Минковского двух множеств называется множество , где обозначает векторную сумму. |
| Определение: |
| Отрицанием множества называется множество , где обозначает векторное отрицание. |
| Теорема: |
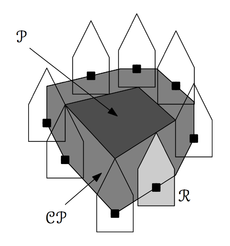
Для заданного робота и препятствия , К-препятствием является множество . |
| Доказательство: |
|
Необходимо доказать, что робот пересекает препятствие в том и только в том случае, если . Пусть робот задевает препятствие, и точка является точкой пересечения. Тогда, так как , то , или . А заметив, что , получаем . В обратную сторону, пусть , тогда существуют точки и такие, что или , а это означает, что пересекает . |
Допустим, для простоты, что робот и все препятствия выпуклые, а позже обобщим для невыпуклых фигур.
| Теорема: |
Пусть заданы две выпуклые фигуры и , с числом вершин и соответственно. Тогда суммой Минковского является выпуклая фигура с не более чем вершинами. |
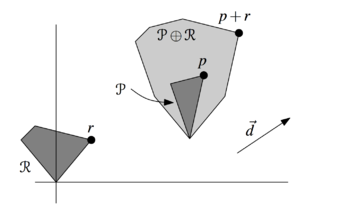
| Доказательство: |
|
Для начала заметим, что любая крайняя точка в направлении вектора есть сумма крайних точек фигур в этом направлении. Убедиться в этом можно спроецировав обе фигуры на вектор . Теперь рассмотрим произвольное ребро из . Оно является крайним в направлении к своей нормали, а значит оно образовано крайними точками фигур, и хотя бы у одной из фигур должно быть ребро, которое является крайним в этом направлении. Сопоставим с этим ребром. Тогда сопоставив таким образом всем ребрам ребра исходных фигур, получаем что всего ребер в не более чем , так как каждое ребро исходных фигур использовалось не более раза. |
Псевдокод
i = j = 0
V[n] = V[0], V[n+1] = V[1], W[m] = W[0], W[m+1] = W[1]
while i < n or j < m do
add V[i]+W[j] to answer
if angle(V[i], V[i+1]) < angle(W[j], W[j+1])
++i
else if angle(V[i], V[i+1]) > angle(W[j], W[j+1])
++j
else
++i, ++j
Здесь множества точек и отсортированы в порядке обхода против часовой стрелки, причем первым элементом в обоих массивах является самая левая нижняя точка множества. Функция angle возвращает значение полярного угла вектора, заданного ее аргументами.
Корректность алгоритма следует из доказательства предыдущей теоремы, а время работы равно , так как на каждой итерации хотя бы один из индексов и увеличивается.
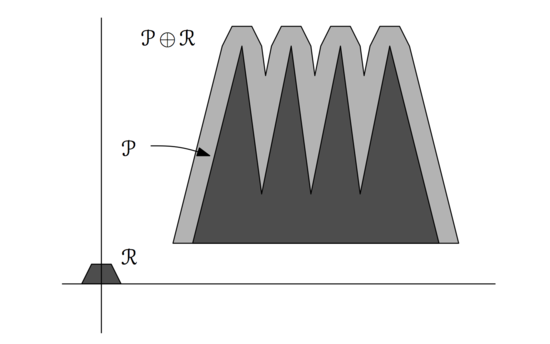
Случай невыпуклых фигур
Для начала заметим следующий факт:
В случае, когда одна из фигур невыпукла, её сначала надо затриангулировать, получив треугольников. После этого, уже известным алгоритмом, надо построить выпуклых фигур с не более чем вершинами, которые будут суммами Минковского соответствующих треугольников. Объединение этих выпуклых фигур будет состоять из вершин.
В случае, когда обе фигуры невыпуклы, обе эти фигуры надо затриангулировать, получив и треугольников соответственно. Построив суммы Минковского множеств этих треугольников получим выпуклых фигур, объединение которых состоит из вершин.
Ссылки
- Английская википедия
- de Berg, van Kreveld, Overmars, Schwarzkopf "Computational Geometry Algorithms and Applications", p. 290