1632
правки
Изменения
м
==Идея алгоритма==Она вскоре стала использоваться с несколькими другими пакетами, что облегчает ее использование в соответствующих сообществах. Теперь у нее есть интеграция с scikit-learn для пользователей Python, а также с пакетом caret для пользователей R. Она также может быть интегрирована в рамах потока данных, таких как Apache Spark<ref>[https://spark.apache.org/ Apache Spark]</ref>, Apache Hadoop<ref>[https://hadoop.apache.org/ Apache Hadoop]<tex/ref>\mathcal{L}^{(t)} = \sum_{i=1}^n l(y_i,\hat{y_i}^{(t-1)}+f_tи Apache Flink<ref>[https://flink.apache.org/ Apache Flink]</ref> с использованием абстрактных Rabit<ref>[https://github.com/dmlc/rabit Rabit]</ref> и XGBoost4J<ref>[https://xgboost.readthedocs.io/en/latest/jvm/ XGBoost JVM]</ref>. Принцип работы XGBoost также был опубликован Тяньцзи Ченом (x_iTianqi Chen))+\Omegaи Карлосом Гастрин (f_tCarlos Guestrin)</tex> {{---}} функция для оптимизации градиентного бустинга.
Дальше с помощью разложения Тейлора ==Описание алгоритма==[[File:golf-MSE.png|700px|thumb|[https://explained.ai/gradient-boosting/images/golf-MSE.png Иллюстрация бустинга]]]В основе '''XGBoost''' лежит алгоритм [[Бустинг, AdaBoost|градиентного бустинга]] [[Дерево решений и случайный лес|деревьев решений]].Градиентный бустинг — это техника машинного обучения для задач классификации и регрессии, которая строит модель предсказания в форме ансамбля слабых предсказывающих моделей, обычно деревьев решений.Обучение ансамбля проводится последовательно в отличие, например от [[Виды_ансамблей | бэггинга]]. На каждой итерации вычисляются отклонения предсказаний уже обученного ансамбля на обучающей выборке. Следующая модель, которая будет добавлена в ансамбль будет предсказывать эти отклонения. Таким образом, добавив предсказания нового дерева к предсказаниям обученного ансамбля мы можем уменьшить среднее отклонение модели, которое является таргетом оптимизационной задачи. Новые деревья добавляются в ансамбль до второго члена можем приблизить это следующим выражением:тех пор,пока ошибка уменьшается, либо пока не выполняется одно из правил "ранней остановки".
Минимум этого выражения относительно Поскольку мы хотим минимизировать ошибку модели на обучающей выборке, нам нужно найти минимум <tex>f_t(x_i)</tex> находится в точке <tex>f_t(x_i) = \fracmathcal{-g_iL}^{h_i(t)}</tex>для каждого ''t''.
2Каждое отдельное дерево ансамбля <tex>f_t(x_i)</tex> обучается стандартным алгоритмом. Пытаемся разбить каждую вершину Для более полного описания см. [[Дерево решений и считаем ''gain''случайный лес|Дерево решений и случайный лес]].
3. Жадно сплитим вершину==Возможности XGBoost=='''Особенности модели'''
from sklearn import datasets==Поддерживаемые интерфейсы== iris = datasets* Интерфейс командной строки (CLI).load_iris* C++ (язык, на котором написана библиотека).* Интерфейс Python, а также модель в Scikit-Learn. X = iris* R интерфейс, а также модель в пакете карета.* Julia.data y = iris* JVM языки, такие как Java, Scala, и платформы, такие как Hadoop.target
rollbackEdits.php mass rollback
'''XGBoost''' <ref>[https://github.com/dmlc/xgboost GitHub project webpage]</ref> {{---}} одна из самых популярных и эффективных реализаций алгоритма [[Бустинг,_AdaBoost|градиентного бустинга]] на деревьях на 2019-й год.
==Основные преимуществаИстория==* Возможность добавлять [XGBoost изначально стартовал как исследовательский проект Тяньцзи Чена (Tianqi Chen) как часть сообщества распределенного глубинного машинного обучения. Первоначально он начинался как терминальное приложение, которое можно было настроить с помощью файла конфигурации libsvm. После победы в Higgs Machine Learning Challenge, он стал хорошо известен в соревновательный кругах по машинному обеспечению. Вскоре после этого были созданы пакеты для Python и R, и теперь у него есть пакеты для многих других языков, таких как Julia, Scala, Java и т. д. Это принесло библиотеке больше разработчиков и сделало ее популярной среди сообщества Kaggle<ref>[Регуляризация|регуляризациюhttps://www.kaggle.com/ Kaggle]]* Возможность работать с разреженными данными* Возможность распределенного обучения* Эффективная реализация</ref>, где она использовалось для большого количества соревнований. Программное обеспечение разработано по методологии SCRUM.
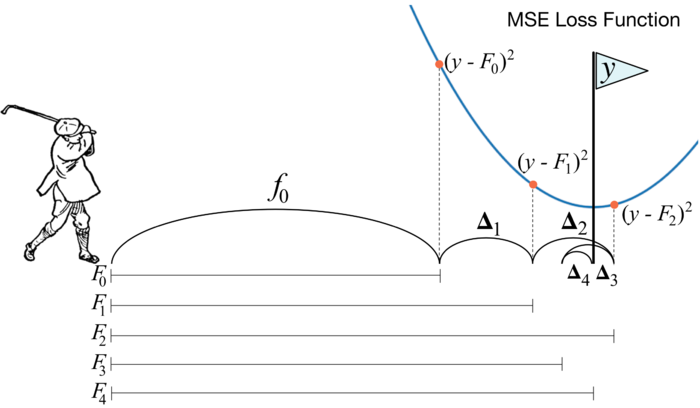
Рассмотрим иллюстрацию бустинга. На ней рассматривается поведение модели на одной точке абстрактной задачи линейной регрессии. Предположим, что первая модель ансамбля <tex>F</tex> всегда выдаетвыборочное среднее предсказываемой величины <tex>f_0</tex>. Такое предсказание довольно грубое, поэтому среднеквадратичное отклонение на выбранной нами точке будет довольно большим. Мы попробуем это исправить обучив модель<tex>\Delta_1</tex>, которая будет "корректировать" предсказание предыдущего ансамбля <tex>F_0</tex>. Таким образом мы получим ансамбль <tex>F_1</tex>, предсказание которого будет суммироваться из предсказаний моделей <tex>f_0</tex> и <tex>\Delta_1</tex>. Продолжая такую последовательность мы приходим к ансамблю <tex>F_4</tex> предсказание которого суммируется из предсказаний <tex>f_0</tex>, <tex>\Delta_1</tex>, <tex>\Delta_2</tex>, <tex>\Delta_3</tex>, <tex>\Delta_4</tex> и предсказывает в точности значение заданного таргета.===Математика за алгоритмом===<tex>\mathcal{L}^{(t)} = \sum_{i=1}^n l(y_i,\hat{y_i}^{(t-1)}+f_t(x_i))+\Omega(f_t)</tex> {{---}} функция для оптимизации градиентного бустинга, где: <tex>l</tex> {{---}} функция потерь, см. [[Общие понятия|Общие понятия]]. <tex>y_i, \hat{y_i}^{t}</tex> {{---}} значение ''i''-го элемента обучающей выборки и сумма предсказаний первых ''t'' деревьев соответственно. <tex>x_i</tex> {{---}} набор признаков ''i''-го элемента обучающей выборки. <tex>f_t</tex> {{---}} функция (в нашем случае дерево), которую мы хотим обучить на шаге ''t''. <tex>f_t(x_i)</tex> {{---}} предсказание на ''i''-ом элементе обучающей выборки. <tex>\Omega(f)</tex> {{---}} регуляризация функции <tex>f</tex>. <tex>\Omega(f) = \gamma T + \frac{1}{2} \lambda \lVert w \rVert ^2</tex>, где T {{---}} количество вершин в дереве,<tex>w</tex> {{---}} значения в листьях, а <tex>\gamma</tex> и <tex>\lambda</tex> {{---}} параметры регуляризации. Дальше с помощью разложения Тейлора до второго члена можем приблизить оптимизируемую функцию <tex>\mathcal{L}^{(t)}</tex> следующим выражением: <tex>\mathcal{L}^{(t) } = \sum_{i=1}^n l(y_i,\hat{y_i}^{(t-1)} + g_i f_t(x_i) + 0.5 h_i f_t^2(x_i)) + \Omega(f_t)</tex>, где
<tex>g_i = \frac {\partial {l(y_i,\hat{y_i}^{t-1})}}{\partial{\hat{y_i}^{t-1}}}</tex>, <tex>h_i = \frac {\partial^2 {l(y_i,\hat{y_i}^{t-1})}}{\partial^2{\hat{y_i}^{t-1}}}</tex>
Минимум этого выражения относительно <tex>f_t(x_i)</tex> находится в точке <tex>f_t(x_i) ===Процесс обучение отдельного дерева===1\frac{-g_i}{h_i}</tex>. Изначально дерево содержит единственную вершину
XGBoost поддерживает все возможности таких библиотек как scikit-learn с возможностью добавлять регуляризацию. Поддержаны три главные формы градиетного бустинга: * Стандартный [[Бустинг,_AdaBoost|градиентный бустинг]] с возможностью изменения скорости обучения(''learning rate'').* Стохастический градиентный бустинг<ref>[https://statweb.stanford.edu/~jhf/ftp/stobst.pdf Stochastic Gradient Boosting]</ref> с возможностью семплирования по строкам и колонкам датасета.* Регуляризованный градиентный бустинг<ref>[https://arxiv.org/pdf/1806.09762.pdf Regularized Gradient Boosting]</ref> с L1 и L2 регуляризацией. '''Системные функции''' Библиотека предоставляет систему для использования в различных вычислительных средах: * Параллелизация построения дерева с использованием всех ваших ядер процессора во время обучения.* Распределенные вычисления для обучения очень крупных моделей с использованием кластера машин.* Вычисления для очень больших наборов данных, которые не вписываются в память.* Кэш Оптимизация структуры данных и алгоритма для наилучшего использования аппаратного обеспечения. '''Особенности алгоритма''' Реализация алгоритма была разработана для эффективности вычислительных ресурсов времени и памяти. Цель проекта заключалась в том, чтобы наилучшим образом использовать имеющиеся ресурсы для обучения модели. Некоторые ключевые функции реализации алгоритма включают: * Различные стратегии обработки пропущенных данных.* Блочная структура для поддержки распараллеливания обучения деревьев.* Продолжение обучения для дообучения на новых данных. ==Пример использования с помощью библиотеки xgboostОсновные параметры==* ''n_estimators'' {{---}} число деревьев.* ''eta'' {{---}} размер шага. Предотвращает переобучение.* ''gamma'' {{---}} минимальное изменение значения ''loss'' функции для разделения листа на поддеревья.* ''max_depth'' {{---}} максимальная глубина дерева.* ''lambda''/''alpha'' {{---}} ''L2''/''L1'' регуляризация. Для более полного описания параметров модели см. документацию<ref>[https://xgboost.readthedocs.io/en/latest/parameter.html XGBoost Parameters]</ref>.
==Пример использования с помощью библиотеки xgboost==Загрузка датасета. '''from ''' sklearn.cross_validation '''import train_test_split''' datasets X_train, X_test, y_train, y_test iris = train_test_splitdatasets.'''load_iris'''() X, = iris.'''data''' y, test_size=0iris.2, random_state=42)'''target'''
Разделение датасета на обучающую/тестовую выборку. '''from''' sklearn.cross_validation '''import xgboost as xgb''' train_test_split X_train, X_test, y_train, y_test = '''train_test_split'''(X, y, test_size=0.2, random_state=42)
Импорт ''XGBoost'' и создание необходимых объектов. '''import''' xgboost as xgb dtrain = xgb.'''DMatrix'''(X_train, label=y_train) dtest = xgb.'''DMatrix'''(X_test, label=y_test)
Задание параметров модели.
param = {
'max_depth': 3, # максимальная глубина дерева 'eta': 0.3, # параметр обучения
'silent': 1,
'objective': 'multi:softprob', # функция потерь 'num_class': 3} # число классов num_round = 20 # число итераций
Обучение. bst = xgb.'''train'''(param, dtrain, num_round) preds = bst.'''predict'''(dtest)
Определение качества модели на тестовой выборке. '''import ''' numpy '''as ''' np '''from ''' sklearn.metrics '''import ''' precision_score
best_preds = np.asarray([np.argmax(line) for line in preds])
'''print ''' precision_score(y_test, best_preds, average='macro') ==См. также==*[[:Дерево решений и случайный лес|Дерево решений и случайный лес]]*[[:Бустинг, AdaBoost|Бустинг, AdaBoost]] ==Примечания==<references/>== Источники информации ==* [https://arxiv.org/abs/1603.02754 Tianqi Chen, Carlos Guestrin. XGBoost: A Scalable Tree Boosting System]* [https://towardsdatascience.com/xgboost-mathematics-explained-58262530904a XGBoost Mathematics Explained]* [https://medium.com/@gabrieltseng/gradient-boosting-and-xgboost-c306c1bcfaf5 Gradient Boosting and XGBoost]* [https://machinelearningmastery.com/gentle-introduction-xgboost-applied-machine-learning/ A Gentle Introduction to XGBoost for Applied Machine Learning] [[Категория: Машинное обучение]][[Категория: Ансамбли]]
