Корреляция случайных величин — различия между версиями
м (rollbackEdits.php mass rollback) |
|||
| (не показано 8 промежуточных версий 4 участников) | |||
| Строка 1: | Строка 1: | ||
{{Определение | {{Определение | ||
|definition= | |definition= | ||
| − | Среднеквадратичным отклонением <tex>\sigma_{\eta}</tex> называется величина, равная квадратному корню из [[Дисперсия_случайной_величины | дисперсии]] случайной величины <tex>\eta</tex> | + | <b>Среднеквадратичным отклонением</b> (англ. ''standart deviation'') <tex>\sigma_{\eta}</tex> называется величина, равная квадратному корню из [[Дисперсия_случайной_величины | дисперсии]] случайной величины <tex>\eta</tex> |
: <tex>\sigma_{\eta}=\sqrt{D(\eta)}</tex> | : <tex>\sigma_{\eta}=\sqrt{D(\eta)}</tex> | ||
}} | }} | ||
| Строка 7: | Строка 7: | ||
|definition= | |definition= | ||
Пусть <tex>\eta,\xi</tex> {{---}} две [[Дискретная_случайная_величина | случайные величины]], определённые на одном и том же вероятностном пространстве. Тогда <b> корреляцией случайных величин </b> (англ. correlation) <tex>\eta</tex> и <tex>\xi</tex> называется выражение следующего вида: | Пусть <tex>\eta,\xi</tex> {{---}} две [[Дискретная_случайная_величина | случайные величины]], определённые на одном и том же вероятностном пространстве. Тогда <b> корреляцией случайных величин </b> (англ. correlation) <tex>\eta</tex> и <tex>\xi</tex> называется выражение следующего вида: | ||
| − | : <tex>\mathrm{Corr}(\eta,\xi)=\dfrac{\mathrm{Cov}(\eta,\xi)}{\sigma_{\eta} | + | : <tex>\mathrm{Corr}(\eta,\xi)=\dfrac{\mathrm{Cov}(\eta,\xi)}{\sigma_{\eta}\sigma_{\xi}}</tex>, где <tex>\mathrm{Cov}(\eta,\xi)</tex> {{---}} [[Ковариация_случайных_величин | ковариация случайных величин]]. |
}} | }} | ||
== Вычисление == | == Вычисление == | ||
| − | Заметим, что <tex>\sigma_{\xi} = \sqrt{D(\xi)} = E\big((\xi-E(\xi))^2\big)</tex> - среднеквадратичное отклонение. | + | Заметим, что <tex>\sigma_{\xi} = \sqrt{D(\xi)} = E\big((\xi-E(\xi))^2\big)</tex> {{---}} среднеквадратичное отклонение. |
| − | : <tex>\mathrm{Corr}(\eta,\xi)=\dfrac{\mathrm{Cov}(\eta,\xi)}{\sigma_{\eta} | + | : <tex>\mathrm{Corr}(\eta,\xi)=\dfrac{\mathrm{Cov}(\eta,\xi)}{\sigma_{\eta} \sigma_{\xi}} = \dfrac{E\big((\eta-E\eta)(\xi-E\xi)\big)}{{\sqrt{D(\eta)} \sqrt{D(\xi)}}} =\dfrac{E(\xi \eta) - E(\xi) E(\eta)}{{\sigma_{\eta} \sigma_{\xi}}}</tex> |
== Корреляция и взаимосвязь величин == | == Корреляция и взаимосвязь величин == | ||
| Строка 23: | Строка 23: | ||
: <tex>\mathrm{Corr}(\eta,\xi) = \mathrm{Corr}(\xi,\eta)</tex>. | : <tex>\mathrm{Corr}(\eta,\xi) = \mathrm{Corr}(\xi,\eta)</tex>. | ||
|proof= | |proof= | ||
| − | : <tex>\mathrm{Corr}(\eta,\xi) = \dfrac{ E(\eta | + | : <tex>\mathrm{Corr}(\eta,\xi) = \dfrac{ E(\eta \xi) - E(\eta) E(\xi)}{\sqrt{D(\eta)} \sqrt{D(\xi)} } = \dfrac{ E(\xi \eta) - E(\xi) E(\eta)}{\sqrt{D(\xi)} \sqrt{D(\eta)} } = \mathrm{Corr}(\xi,\eta)</tex>. |
}} | }} | ||
| Строка 30: | Строка 30: | ||
Корреляция случайной величины с собой равна <tex>1</tex>. | Корреляция случайной величины с собой равна <tex>1</tex>. | ||
|proof= | |proof= | ||
| − | : <tex>\mathrm{Corr}(\eta,\eta) = \dfrac{ E(\eta | + | : <tex>\mathrm{Corr}(\eta,\eta) = \dfrac{ E(\eta \eta) - E(\eta) E(\eta)}{\sqrt{D(\eta)} \sqrt{D(\eta)} } = \dfrac{D(\eta)}{D(\eta)} = 1</tex> |
}} | }} | ||
| Строка 37: | Строка 37: | ||
Корреляция лежит на отрезке <tex>[-1, 1]</tex>. | Корреляция лежит на отрезке <tex>[-1, 1]</tex>. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
}} | }} | ||
| Строка 56: | Строка 45: | ||
Если <tex> \mathrm{Corr}(\eta, \xi) = \pm 1 </tex>, то <tex>\eta</tex> и <tex>\xi</tex> линейно зависимы. | Если <tex> \mathrm{Corr}(\eta, \xi) = \pm 1 </tex>, то <tex>\eta</tex> и <tex>\xi</tex> линейно зависимы. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
}} | }} | ||
| Строка 77: | Строка 52: | ||
Если <tex>\eta</tex> и <tex>\xi</tex> линейно зависимы, то <tex>\mathrm{Corr}(\eta, \xi)= \pm 1 </tex>. | Если <tex>\eta</tex> и <tex>\xi</tex> линейно зависимы, то <tex>\mathrm{Corr}(\eta, \xi)= \pm 1 </tex>. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
}} | }} | ||
| Строка 95: | Строка 59: | ||
Если <tex>\eta,\xi</tex> независимые случайные величины, то <tex>\mathrm{Corr}(\eta,\xi) = 0</tex>. | Если <tex>\eta,\xi</tex> независимые случайные величины, то <tex>\mathrm{Corr}(\eta,\xi) = 0</tex>. | ||
|proof= | |proof= | ||
| − | Пусть <tex>\eta</tex> и <tex>\xi</tex> {{---}} [[Независимые_случайные_величины|независимые величины]]. Тогда <tex>E(\eta | + | Пусть <tex>\eta</tex> и <tex>\xi</tex> {{---}} [[Независимые_случайные_величины|независимые величины]]. Тогда <tex>E(\eta \xi)=E(\eta) E(\xi)</tex>, где <tex>E</tex> {{---}} их [[Математическое_ожидание_случайной_величины|математическое ожидание]]. Получаем: |
| − | : <tex>\mathrm{Corr}(\eta, \xi) = \dfrac{E(\xi) | + | : <tex>\mathrm{Corr}(\eta, \xi) = \dfrac{E(\xi) E(\eta) - E(\xi) E(\eta)}{{E\big((\eta-E(\eta))^2\big) E\big((\xi-E(\xi))^2\big)}} = 0</tex> |
<b>Но обратное неверно:</b> | <b>Но обратное неверно:</b> | ||
| − | Пусть <tex>\eta</tex> {{---}} [[Дискретная_случайная_величина|случайная величина]], распределенная симметрично около 0, а <tex>\xi=\eta^2</tex>. <tex>\mathrm{Corr}(\eta,\xi)=0</tex>, но <tex>\eta</tex> и <tex>\xi</tex> {{---}} зависимые величины. | + | Пусть <tex>\eta</tex> {{---}} [[Дискретная_случайная_величина|случайная величина]], распределенная симметрично около <tex>0</tex>, а <tex>\xi=\eta^2</tex>. <tex>\mathrm{Corr}(\eta,\xi)=0</tex>, но <tex>\eta</tex> и <tex>\xi</tex> {{---}} зависимые величины. |
}} | }} | ||
| Строка 106: | Строка 70: | ||
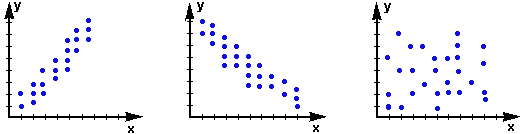
[[Файл:Пример_графиков_корреляции.png|600px|thumb|right|3 диаграммы рассеивания двух случайных величин <tex>X</tex> и <tex>Y</tex>]] | [[Файл:Пример_графиков_корреляции.png|600px|thumb|right|3 диаграммы рассеивания двух случайных величин <tex>X</tex> и <tex>Y</tex>]] | ||
| − | + | #Соответственно, на '''первом графике''' изображена '''положительная корреляция''', когда увеличение <tex>Y</tex> ведет к постепенному увеличению <tex>X</tex>. | |
| − | + | #'''Второй график''' отображает '''отрицательную корреляцию''', когда увеличение <tex>X</tex> воздействует на постепенное уменьшение <tex>Y</tex>. | |
| − | + | #'''Третий график''' показывает, что <tex>X</tex> и <tex>Y</tex> связаны слабо, их распределение не зависит от изменения друг друга, поэтому корреляция между ними будет '''равна <tex>0</tex>'''. | |
| − | |||
| − | |||
=== Определение корреляции по таблице === | === Определение корреляции по таблице === | ||
| − | Рассмотрим 2 случайные величины: курс акций нефтедобывающей компании (<tex>X</tex>) и цены на нефть (<tex>Y</tex>). | + | Рассмотрим <tex>2</tex> случайные величины: курс акций нефтедобывающей компании (<tex>X</tex>) и цены на нефть (<tex>Y</tex>). |
{| class="wikitable" | {| class="wikitable" | ||
|- | |- | ||
! X | ! X | ||
| − | | 2003,6 || 2013,2 || 2007,6 || 2007,4 || 2039,9 || 2025 || 2007 || 2017 || 2015,6 || 2011 | + | | <tex>2003,6</tex> || <tex>2013,2</tex> || <tex>2007,6</tex> || <tex>2007,4</tex> || <tex>2039,9</tex> || <tex>2025</tex> || <tex>2007</tex> || <tex>2017</tex> || <tex>2015,6</tex> || <tex>2011</tex> |
|- | |- | ||
! Y | ! Y | ||
| − | | 108,4 || 107,96 || 108,88 || 110,44 || 110,2 || 108,97 || 109,15 || 108,8 || 111,2 || 110,23 | + | | <tex>108,4</tex> || <tex>107,96</tex> || <tex>108,88</tex> || <tex>110,44</tex> || <tex>110,2</tex> || <tex>108,97</tex> || <tex>109,15</tex> || <tex>108,8</tex> || <tex>111,2</tex> || <tex>110,23</tex> |
|- | |- | ||
|} | |} | ||
| Строка 134: | Строка 96: | ||
<tex>D(Y) = 0,959661</tex> | <tex>D(Y) = 0,959661</tex> | ||
| − | Используя формулу, <tex>\mathrm{Corr}(\eta,\xi)=\dfrac{E(\xi | + | Используя формулу, <tex>\mathrm{Corr}(\eta,\xi)=\dfrac{E(\xi \eta) - E(\xi)E(\eta)}{{\sigma_{\eta} \sigma_{\xi}}}</tex> определяем, что корреляция между величинами <tex>X</tex> и <tex>Y</tex> составляет <tex>0,240935496</tex>, то есть <tex>24\%</tex>. |
== См. также == | == См. также == | ||
Текущая версия на 19:42, 4 сентября 2022
| Определение: |
| Среднеквадратичным отклонением (англ. standart deviation) называется величина, равная квадратному корню из дисперсии случайной величины
|
| Определение: |
Пусть — две случайные величины, определённые на одном и том же вероятностном пространстве. Тогда корреляцией случайных величин (англ. correlation) и называется выражение следующего вида:
|
Содержание
Вычисление
Заметим, что — среднеквадратичное отклонение.
Корреляция и взаимосвязь величин
Значительная корреляция между случайными величинами всегда означает, что присутствует некая взаимосвязь между значениями конкретной выборки, но при другой выборке связь вполне может отсутствовать. Поэтому при нахождении взаимосвязи не нужно делать поспешных выводов о причинно-следственном характере величин, а следует рассмотреть наиболее полную выборку, чтобы делать какие-либо выводы. Коэффициенты корреляции устанавливают лишь статистические взаимосвязи, но не более того.
Свойства корреляции
| Утверждение: |
Корреляция симметрична:
|
|
| Утверждение: |
Корреляция случайной величины с собой равна . |
|
|
| Утверждение: |
Корреляция лежит на отрезке . |
| Утверждение: |
Если , то и линейно зависимы. |
| Утверждение: |
Если и линейно зависимы, то . |
| Утверждение: |
Если независимые случайные величины, то . |
|
Пусть и — независимые величины. Тогда , где — их математическое ожидание. Получаем: Но обратное неверно: Пусть — случайная величина, распределенная симметрично около , а . , но и — зависимые величины. |
Примеры
В общем смысле корреляция — это зависимость между случайными величинами, когда изменение одной влечет изменение распределения другой.
Определение корреляции по диаграмме
- Соответственно, на первом графике изображена положительная корреляция, когда увеличение ведет к постепенному увеличению .
- Второй график отображает отрицательную корреляцию, когда увеличение воздействует на постепенное уменьшение .
- Третий график показывает, что и связаны слабо, их распределение не зависит от изменения друг друга, поэтому корреляция между ними будет равна .
Определение корреляции по таблице
Рассмотрим случайные величины: курс акций нефтедобывающей компании () и цены на нефть ().
| X | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Y |
Для упрощения вычислений определим и как равновероятные случайные величины. Тогда их математическое ожидание и дисперсию легко посчитать:
Используя формулу, определяем, что корреляция между величинами и составляет , то есть .